Relaciones entre conjuntos (parte 1)
Summary
TLDREn este video, se repasan conceptos fundamentales sobre relaciones en teoría de conjuntos. Se explica el producto cartesiano, cómo se definen las relaciones como subconjuntos de este producto y cómo representarlas mediante diagramas de Venn, tablas y gráficos cartesianos. También se aborda la noción de función, sus características (existencia y unicidad), y cómo clasificar funciones como inyectivas, sobreyectivas o biyectivas. Además, se introducen temas como las relaciones inversas, complementarias y la clasificación de funciones. Finalmente, se mencionan las representaciones matriciales para relaciones y su conexión con los isomorfismos entre conjuntos.
Takeaways
- 😀 El producto cartesiano de dos conjuntos A y B es el conjunto de pares ordenados (x, y) donde x pertenece a A y y a B.
- 😀 Una relación es cualquier subconjunto del producto cartesiano entre dos conjuntos, denotada como R, donde A es el conjunto de partida y B el conjunto de llegada.
- 😀 El dominio de una relación incluye todos los elementos de A que están relacionados con al menos un elemento de B.
- 😀 La imagen de una relación está formada por los elementos de B que están relacionados con al menos un elemento de A.
- 😀 La relación inversa o recíproca de una relación R, denotada como R⁻¹, contiene los pares (y, x) en lugar de (x, y).
- 😀 La relación complementaria de una relación R incluye todos los pares que no están en R pero sí en el producto cartesiano A × B.
- 😀 Una función es un tipo especial de relación que cumple con dos condiciones: existencia (cada elemento de A tiene una imagen) y unicidad (la imagen de cada elemento es única).
- 😀 Una función inyectiva asegura que elementos diferentes de A tienen imágenes distintas en B.
- 😀 Una función sobreyectiva cubre todo el conjunto B, es decir, su conjunto imagen coincide con B.
- 😀 Una función biyectiva es una función que es simultáneamente inyectiva y sobreyectiva, es decir, cada elemento de A se relaciona con uno y solo un elemento de B, y cubre todo el conjunto B.
- 😀 La cantidad de relaciones posibles entre dos conjuntos finitos es 2 elevado a la potencia del producto de sus cardinales, lo que da lugar a un número considerable de subconjuntos posibles del producto cartesiano.
Q & A
¿Qué es el producto cartesiano y cómo se forma?
-El producto cartesiano de dos conjuntos A y B es un conjunto formado por todos los pares ordenados (x, y) donde x pertenece a A y y pertenece a B. Se denota como A × B y está formado por todos los pares posibles que se pueden formar con un elemento de A y uno de B.
¿Qué se entiende por una relación entre dos conjuntos?
-Una relación entre dos conjuntos A y B es cualquier subconjunto del producto cartesiano A × B. Es decir, es un conjunto de pares ordenados en los cuales el primer elemento pertenece a A y el segundo a B.
¿Cómo se puede representar una relación entre conjuntos?
-Se puede representar de varias maneras: por extensión (como un conjunto de pares ordenados), mediante diagramas de Venn, con tablas de relaciones o gráficos cartesianos. En algunos casos, como con conjuntos infinitos, se utilizan curvas para representar las relaciones.
¿Qué es el dominio de una relación?
-El dominio de una relación es el conjunto de todos los elementos del primer conjunto A que están relacionados con al menos un elemento del segundo conjunto B. Es decir, son los elementos de A que aparecen en los pares ordenados de la relación.
¿Qué es la imagen de una relación?
-La imagen de una relación es el conjunto de todos los elementos del segundo conjunto B que están relacionados con al menos un elemento del primer conjunto A. Es decir, son los elementos de B que aparecen como segundos componentes en los pares de la relación.
¿Qué diferencia existe entre la relación inversa y la complementaria?
-La relación inversa de una relación R de A en B, denotada como R⁻¹, consiste en invertir los pares ordenados, es decir, se intercambia el primer y el segundo elemento de cada par. La relación complementaria, por otro lado, incluye todos los pares del producto cartesiano A × B que no están en la relación R original.
¿Qué condiciones debe cumplir una relación para ser una función?
-Para que una relación sea una función, debe cumplir dos condiciones: (1) existencia, es decir, cada elemento del primer conjunto A debe estar relacionado con al menos un elemento de B, y (2) unicidad, es decir, cada elemento de A debe estar relacionado con exactamente un único elemento de B.
¿Qué caracteriza a una función inyectiva?
-Una función es inyectiva si cada elemento del conjunto de partida A tiene una imagen distinta en el conjunto de llegada B. Es decir, no pueden existir dos elementos diferentes de A que tengan la misma imagen en B.
¿Qué es una función sobreyectiva?
-Una función es sobreyectiva si el conjunto imagen coincide completamente con el conjunto de llegada B. Es decir, cada elemento de B tiene al menos un elemento de A relacionado con él.
¿Qué es una función biyectiva?
-Una función es biyectiva si es tanto inyectiva como sobreyectiva. Esto significa que cada elemento de A tiene una imagen única en B y, además, todos los elementos de B son imágenes de algún elemento de A.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Relaciones Binarias y digrafos (parte 3)

Notación de Conjuntos por Extensión y Comprensión | Ejemplo 2

Relaciones Matemáticas

La Teoría más LOCA de la Matemática (Teoría de CONJUNTOS)
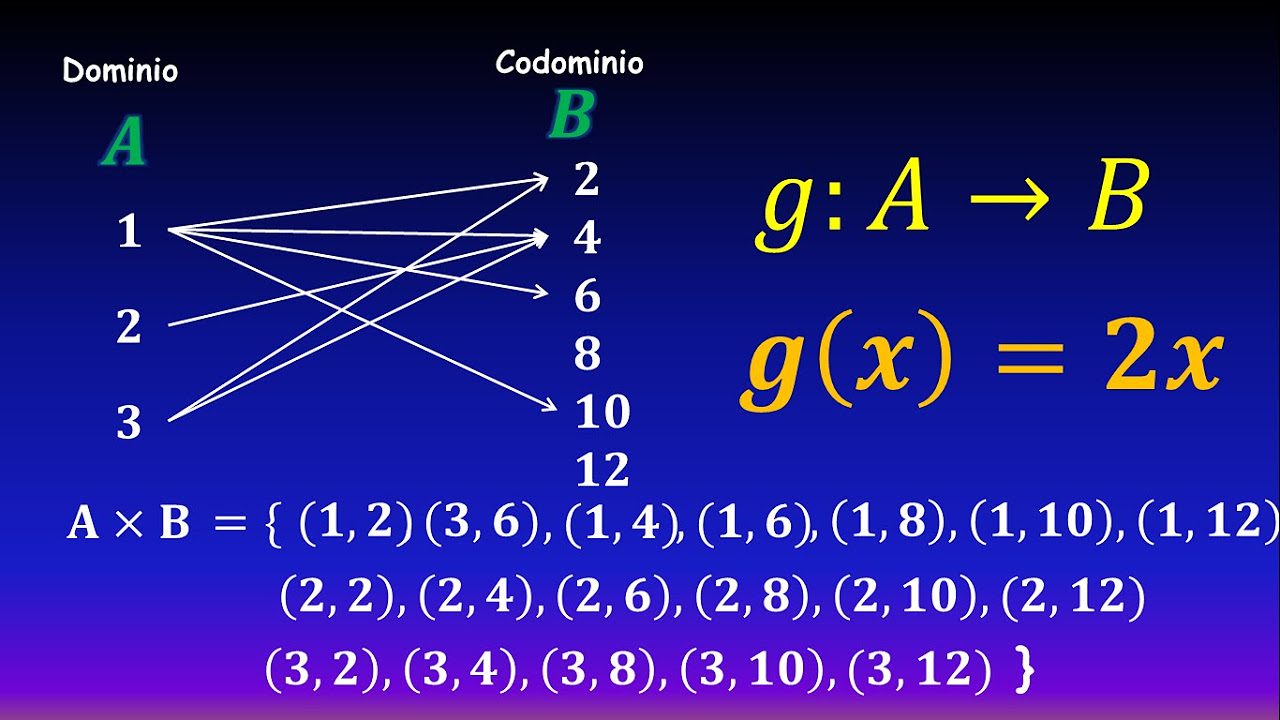
01. ¿Qué es una Función? (Funciones, relaciones, producto cartesiano)

Teoría de GRAFOS en INFORMÁTICA: Que es un grafo, Tipos de Grafos, como representarlos y ejemplos
5.0 / 5 (0 votes)
