How to determine the sum of interior angles for any polygon
Summary
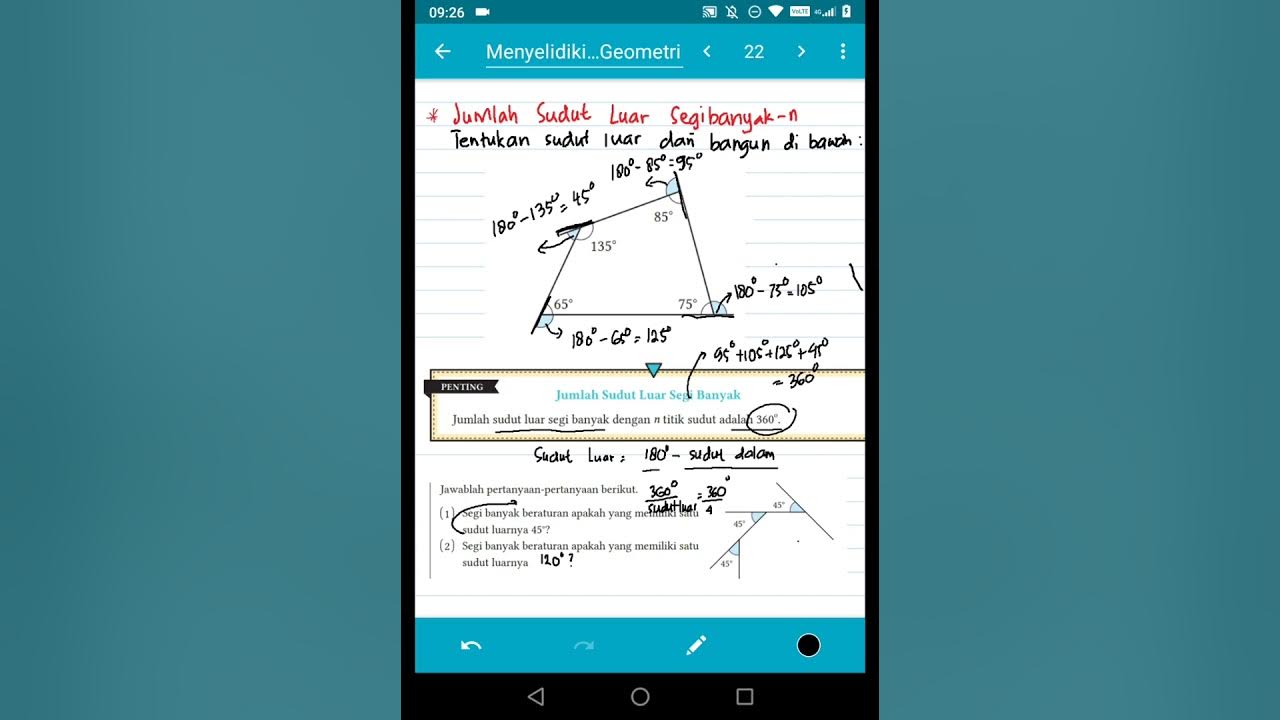
TLDRThis video explains how to determine the sum of the interior angles of any polygon using a simple formula. Starting with the sum of angles in a triangle (180°), the video demonstrates how polygons can be divided into triangles. By subtracting 2 from the number of sides, the number of triangles is found, and multiplying this by 180° gives the sum of the interior angles. This method works for any polygon, whether regular or irregular, and can be applied to polygons with any number of sides.
Takeaways
- 😀 The sum of the interior angles of a triangle is always 180°, regardless of the type of triangle.
- 😀 The sum of the interior angles in polygons is determined by the number of triangles formed from a single vertex.
- 😀 For any polygon, the sum of its interior angles can be found by drawing diagonals from one vertex to the others.
- 😀 In a quadrilateral (4 sides), you can form 2 triangles, so the sum of the interior angles is 360°.
- 😀 In an octagon (8 sides), you can form 6 triangles, so the sum of the interior angles is 1,080°.
- 😀 The number of triangles in any polygon is always equal to the number of sides minus 2.
- 😀 The formula for calculating the sum of the interior angles of any polygon is: (n - 2) × 180°, where n is the number of sides.
- 😀 This formula applies to all polygons, whether they are convex or concave.
- 😀 To calculate the sum of interior angles for polygons with more than 4 sides, use the same formula by plugging in the number of sides.
- 😀 The method shown works for polygons with any number of sides, from triangles to larger polygons with hundreds of sides.
Q & A
What is the sum of interior angles in a triangle?
-The sum of the interior angles of a triangle is always 180°, regardless of the type of triangle (isosceles, equilateral, right, etc.).
How does the number of sides in a polygon relate to the number of triangles that can be formed within it?
-The number of triangles that can be formed within a polygon is equal to the number of sides minus two. For example, a quadrilateral has 4 sides and 2 triangles.
How do you calculate the sum of the interior angles of a polygon?
-To calculate the sum of interior angles of a polygon, subtract 2 from the number of sides to determine the number of triangles, and then multiply the result by 180°.
Why is the number 180° important in the context of this explanation?
-The number 180° represents the sum of the interior angles of a triangle. This value is used to calculate the sum of angles for larger polygons by counting how many triangles can fit inside them.
What does 'n - 2' represent in the formula for calculating the sum of interior angles?
-'n - 2' represents the number of triangles that can be formed by drawing lines from a vertex to all other vertices in the polygon. The number of triangles is always two less than the number of sides.
What does the term 'concave polygon' refer to, and why is it relevant in this method?
-A concave polygon is a polygon where at least one interior angle is greater than 180°. This method of calculating the sum of interior angles works for concave polygons but not for convex polygons.
What is the formula used to find the sum of interior angles of a polygon with 'n' sides?
-The formula to calculate the sum of interior angles of a polygon with 'n' sides is: (n - 2) × 180°.
Can this method be applied to polygons with any number of sides?
-Yes, this method can be applied to polygons with any number of sides, including polygons with as many as 250 sides, as long as the polygon is concave.
What happens if the polygon is convex instead of concave?
-The method for calculating the sum of interior angles is not valid for convex polygons, as the process described only works for concave polygons.
How does this method help in understanding the geometry of polygons?
-This method helps by breaking down complex polygons into simpler triangles, allowing us to calculate the sum of interior angles in a straightforward way using the relationship between sides and triangles.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)