LOGARITMA Kelas 10 Kurikulum Merdeka
Summary
TLDRIn this educational video, the instructor introduces logarithms, explaining their relationship with exponents and their fundamental properties. Viewers learn the definition of logarithms, how to convert exponential equations into logarithmic form, and the proper notation for bases. The video explores various properties of logarithms, including addition, subtraction, and transformations involving exponents. Through numerous examples, the instructor illustrates how to solve logarithmic equations and apply these properties to simplify expressions. The session emphasizes clarity in notation to avoid confusion, making it an essential guide for students aiming to master logarithms.
Takeaways
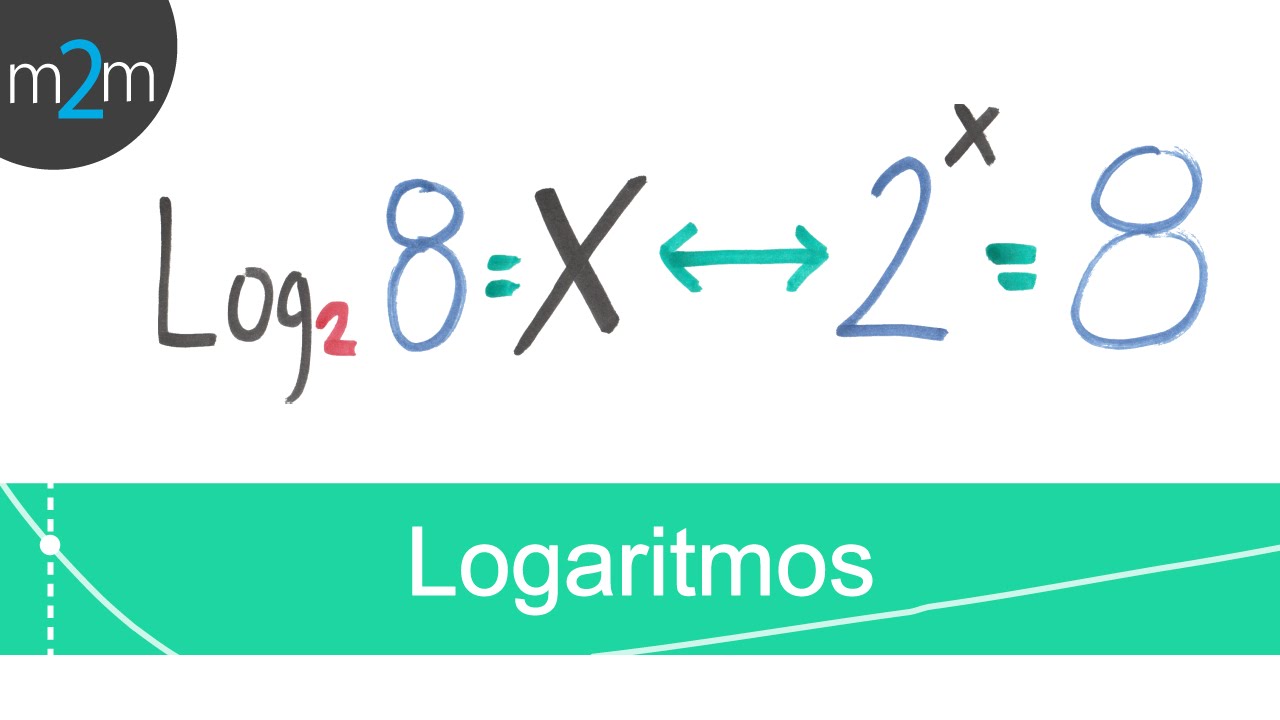
- 😀 Logarithms are used to find the exponent in an exponential equation.
- 😀 The definition of logarithm states that if a^x = b, then log_b(a) = x.
- 😀 Logarithm bases (a) must be greater than 0 and not equal to 1, while the number (b) must be greater than 0.
- 😀 The notation log_b(x) means the logarithm of x with base b.
- 😀 Logarithmic properties include: log_b(xy) = log_b(x) + log_b(y) (for multiplication).
- 😀 For subtraction, log_b(x/y) = log_b(x) - log_b(y) (for division).
- 😀 A power in the numerator can be moved in front as a coefficient: log_b(x^n) = n * log_b(x).
- 😀 When the base is raised to a power, it can also be moved in front, but as a fraction: log_b(a^m) = (m/n) * log_b(a).
- 😀 The change of base formula allows conversion between bases: log_a(b) = 1/log_b(a).
- 😀 The logarithm of a number to itself is always 1, and the logarithm of 1 to any base is always 0.
Q & A
What is the definition of a logarithm as mentioned in the video?
-A logarithm is defined as the exponent to which a base must be raised to produce a given number. It is related to exponentiation.
How do you express the logarithmic form of the equation a^x = b?
-In logarithmic form, a^x = b is expressed as log_b(a) = x.
What are the conditions for the base 'a' and the number 'b' in a logarithmic expression?
-The base 'a' must be greater than 0 and cannot equal 1, while 'b' must be greater than 0.
Can you provide an example of converting an exponential expression to logarithmic form?
-For example, 3^2 = 9 can be converted to logarithmic form as log_3(9) = 2.
What is the property of logarithms related to addition?
-The property states that log_a(b) + log_a(c) = log_a(b * c), meaning you multiply the numbers when adding their logs with the same base.
How do you handle logarithmic expressions that involve subtraction?
-For subtraction, the property states that log_a(b) - log_a(c) = log_a(b / c), meaning you divide the numbers when subtracting their logs with the same base.
What happens to the exponent in a logarithmic expression when the base is raised to a power?
-If you have log_a(b^n), it can be expressed as n * log_a(b), moving the exponent in front of the logarithm.
What is the significance of the change of base formula in logarithms?
-The change of base formula allows you to convert logarithms to a different base, expressed as log_a(b) = log_c(b) / log_c(a), where c is the new base.
How is the logarithm of 1 defined for any base?
-The logarithm of 1 is always 0, regardless of the base, because any number raised to the power of 0 equals 1.
What can be concluded about the logarithm where the base and the argument are the same?
-When the base and the argument are the same, such as log_a(a), the result is always 1, since a raised to the power of 1 equals a.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)