Introduction to Fourier Series - Adding Sine Waves to make Sawtooth, Square, and Triangle Waves
Summary
TLDR这段视频解释了傅里叶级数的概念,展示了如何通过加和不同频率和幅度的正弦波来构建复杂的波形。通过不断增加正弦波的项数,能够得到锯齿波和方波等波形。特别是当只保留奇数项时,得到的波形会趋近于方波。而当保留特定的奇数项并调整系数时,波形会逐渐变得更加尖锐,形成纯粹的锯齿波。视频深入浅出地展示了傅里叶级数在图形上的表现和应用。
Takeaways
- 😀 通过在正弦波前添加不同的系数,可以调节正弦波的振幅和周期。
- 😀 正弦波的振幅表示其波动的高度,周期决定了一个完整波动的时间长度。
- 😀 当我们将不同振幅和周期的正弦波相加时,可以形成更复杂的波形,例如锯齿波。
- 😀 锯齿波的形成是通过将一系列不同的正弦波叠加而成,起始时只是简单的一个正弦波。
- 😀 随着越来越多的正弦波叠加,波形逐渐趋近于锯齿形状,形成尖锐的转折。
- 😀 使用傅里叶级数(Fourier Series)可以通过将一系列正弦波加总,生成任何周期性波形。
- 😀 通过只使用奇数项(如1/1sin(πx), 1/3sin(3πx)等),可以得到方波。
- 😀 方波是通过叠加包含奇数项的傅里叶级数来实现的,随着项数的增加,波形越来越接近真实的方波。
- 😀 当叠加的项数达到50个时,得到的方波已经非常尖锐,几乎是完美的方波。
- 😀 傅里叶级数不仅能够生成锯齿波和方波,还能用于生成许多其他周期性波形,适用于多种应用领域。
Q & A
什么是傅里叶级数?
-傅里叶级数是将一个周期函数表示为一组正弦波的无穷级数。通过适当的加权,正弦波可以合成复杂的波形,如锯齿波或方波。
正弦波的幅度和周期分别是如何定义的?
-正弦波的幅度决定了波的最大振幅,例如幅度为1时,波在+1和-1之间振荡;而周期则是波完成一个完整波动所需的时间或距离。在该脚本中,周期为2。
如何通过傅里叶级数生成锯齿波?
-通过将多个不同幅度和周期的正弦波相加,并持续增加正弦波的数量,最终得到一个锐角的锯齿波形。随着更多正弦波的加入,波形逐渐接近一个锐角的锯齿波。
如何通过傅里叶级数生成方波?
-通过仅使用傅里叶级数中的奇数项(如sin(1πx), sin(3πx), sin(5πx)等),并且每一项的系数按照1/n²的比例递减,可以生成方波。
傅里叶级数中的奇数项和偶数项有什么区别?
-奇数项(如sin(1πx), sin(3πx)等)用于生成方波,而偶数项(如sin(2πx), sin(4πx)等)不参与方波的形成,而是生成其他类型的波形。
在傅里叶级数中,正弦波的系数是如何决定的?
-正弦波的系数通常与频率有关,常见的系数是1/n(n为整数),或者在某些情况下使用1/n²,目的是调整每个正弦波的幅度,以便产生预期的波形。
如何理解正弦波加法对波形的影响?
-通过将不同频率和不同幅度的正弦波叠加在一起,我们可以合成出各种波形。例如,多个正弦波相加可以得到像锯齿波、方波或其他更复杂的波形。
傅里叶级数如何通过加法生成更复杂的波形?
-傅里叶级数通过将不同频率的正弦波叠加形成复杂的波形。通过逐步增加正弦波的数量,波形会逐渐接近目标波形,例如锯齿波或方波。
在傅里叶级数的表达式中,n的作用是什么?
-在傅里叶级数中,n表示正弦波的频率倍数。例如,sin(πx)表示第一项,sin(2πx)表示第二项,以此类推。n的增加意味着更高的频率,导致波形的变化。
为什么只有奇数项可以生成方波?
-奇数项(如sin(1πx), sin(3πx)等)生成方波的原因是它们在波形中产生尖锐的变化,而偶数项会产生更平滑的波形,无法形成方波的快速跳变。
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
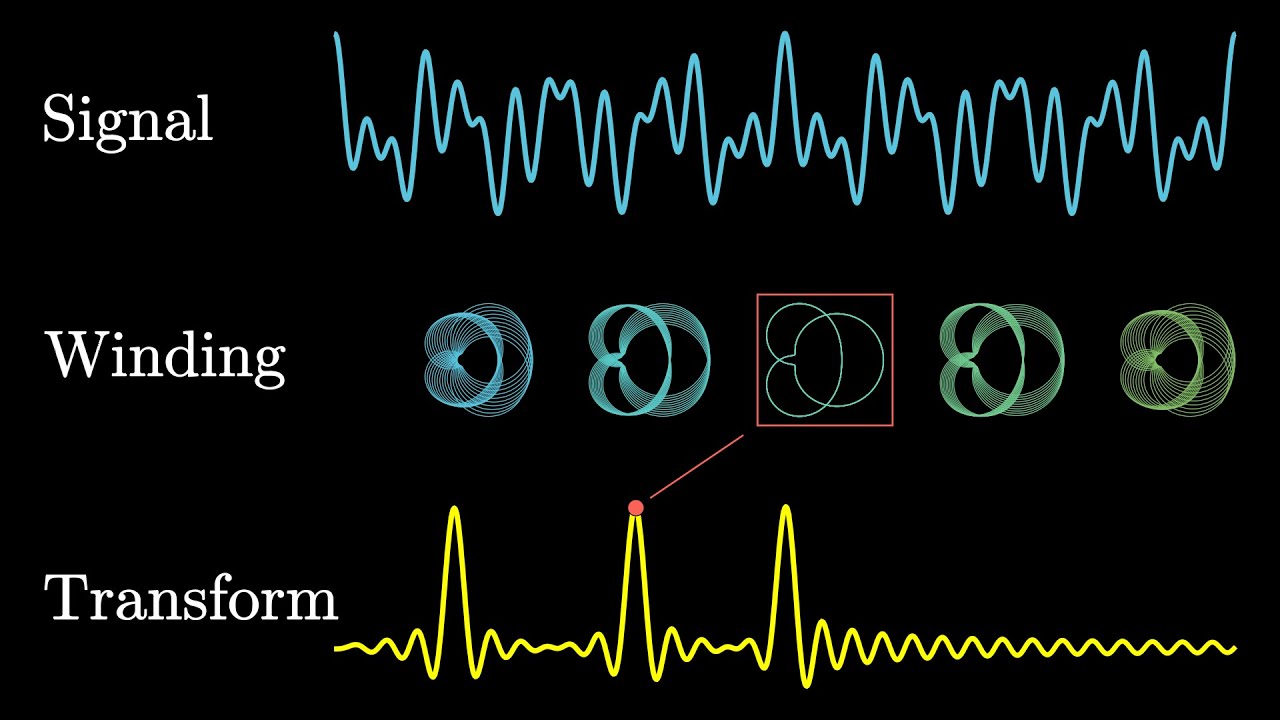
But what is the Fourier Transform? A visual introduction.

How a Lens creates an Image.

Combination of two vibration signals (sum of two signals)

Crypto Explained with Bananas

Hibridación del carbono

Visual Guide to Transformer Neural Networks - (Episode 1) Position Embeddings

LangGraph Crash Course with code examples
5.0 / 5 (0 votes)
