Sistemas de ecuaciones lineales 2x2 | Método de Sustitución | Ejemplo 1
Summary
TLDREn este video, se presenta un método didáctico para resolver sistemas de ecuaciones lineales de 2x2 utilizando el método de sustitución. El instructor explica con detalle cada paso, comenzando por despejar una variable en una ecuación, reemplazando esa variable en la otra ecuación y finalmente resolviendo la ecuación resultante para encontrar los valores de las variables. A través de un ejemplo ilustrativo y un enfoque paso a paso, los espectadores pueden comprender claramente cómo abordar problemas similares y verificar sus soluciones. Además, se ofrecen recomendaciones para elegir la variable a despejar y sugerencias para una solución más eficiente.
Takeaways
- 📘 El curso trata sobre sistemas de ecuaciones lineales de 2x2 y explica en detalle el método de sustitución.
- 🔍 Se aborda un ejemplo de solución de un sistema de ecuaciones usando el método de sustitución paso a paso.
- 📌 El método de sustitución implica reemplazar una de las variables en una de las ecuaciones por su valor determinado.
- 🤔 Se recomienda despejar una variable que esté positiva y sola en una ecuación para simplificar el proceso.
- 📑 En el primer paso, se despeja una letra en una ecuación, dejando una ecuación con una sola variable.
- 🔄 El segundo paso es reemplazar la variable despejada en la otra ecuación por su valor.
- 🧩 El tercer paso consiste en resolver la ecuación con una sola variable obtenida en el paso anterior.
- 🔢 A continuación, se realiza el paso de pasar las letras a un lado y los números al otro para simplificar la ecuación.
- 📐 El cuarto paso es reemplazar la variable resuelta en una de las ecuaciones para encontrar el valor de la otra variable.
- 📈 El script ofrece un ejemplo práctico para que los estudiantes puedan entender y aplicar el método de sustitución.
- 🎓 Se invita a los estudiantes a practicar y verificar los resultados reemplazando las variables en ambas ecuaciones para obtener igualdad verdadera.
Q & A
¿Qué es el método de sustitución en sistemas de ecuaciones lineales de 2x2?
-El método de sustitución es un proceso para resolver sistemas de ecuaciones lineales de 2x2, en el cual se reemplaza una variable en una de las ecuaciones por su valor determinado de la otra ecuación, con el objetivo de simplificar el sistema y encontrar la solución.
¿Cuál es el primer paso para resolver un sistema de ecuaciones lineales por el método de sustitución?
-El primer paso es despejar una letra, es decir, una variable, en una de las ecuaciones del sistema, dejando así una ecuación con solo una variable.
¿Cómo se debe reemplazar la letra despejada en el otro sistema de ecuaciones?
-La letra despejada en la primera ecuación debe ser reemplazada con su valor correspondiente en la segunda ecuación, para así poder continuar con el proceso de resolución del sistema.
¿Qué se debe hacer después de reemplazar la letra en la otra ecuación?
-Después de reemplazar la letra, se debe resolver la nueva ecuación que queda, la cual tiene solo una variable, para encontrar su valor.
¿Cómo se determina el valor de la segunda variable en el sistema de ecuaciones?
-El valor de la segunda variable se determina al resolver la ecuación que queda después de reemplazar la primera variable en la segunda ecuación del sistema.
¿Qué se hace con los valores de las variables una vez que se han encontrado?
-Una vez que se han encontrado los valores de las variables, se recomienda verificar que los valores satisfagan ambas ecuaciones originales del sistema, asegurando así que la solución es correcta.
¿Qué sucede si una variable está positiva y está sola en una ecuación?
-Si una variable está positiva y está sola en una ecuación, es recomendable despejar esa variable en esa ecuación, ya que simplifica el proceso de resolución del sistema de ecuaciones.
¿Cómo se manejan los términos con variables en la ecuación al reemplazar una letra?
-Cuando se reemplaza una letra en la ecuación, se debe asegurarse de incluir los términos con variables en un paréntesis, de modo que se respeten los signos y se pueda continuar con la resolución del sistema de ecuaciones.
¿Qué se debe hacer al final del proceso de resolución por el método de sustitución?
-Al final del proceso de resolución, se deben verificar los valores de las variables en las ecuaciones originales para confirmar que la solución es correcta y que las ecuaciones se mantienen equilibradas.
¿Cuál es la ventaja de despejar una variable que esté positiva y sola en una ecuación?
-La ventaja de despejar una variable que esté positiva y sola en una ecuación es que simplifica el proceso de resolución, ya que permite obtener una ecuación con una sola variable más rápidamente y facilita el paso siguiente de reemplazo en la otra ecuación.
¿Qué ocurre si se resuelve una ecuación y se encuentra que tiene más de una solución posible?
-Si se resuelve una ecuación y se encuentra que tiene más de una solución posible, esto indica que el sistema de ecuaciones puede tener múltiples soluciones o que puede ser inconsistente. En tales casos, se debe analizar a fondo el sistema para determinar la naturaleza de las soluciones encontradas.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Sistemas de ecuaciones lineales 2x2 | Método de Sustitución | Ejemplo 2

Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción
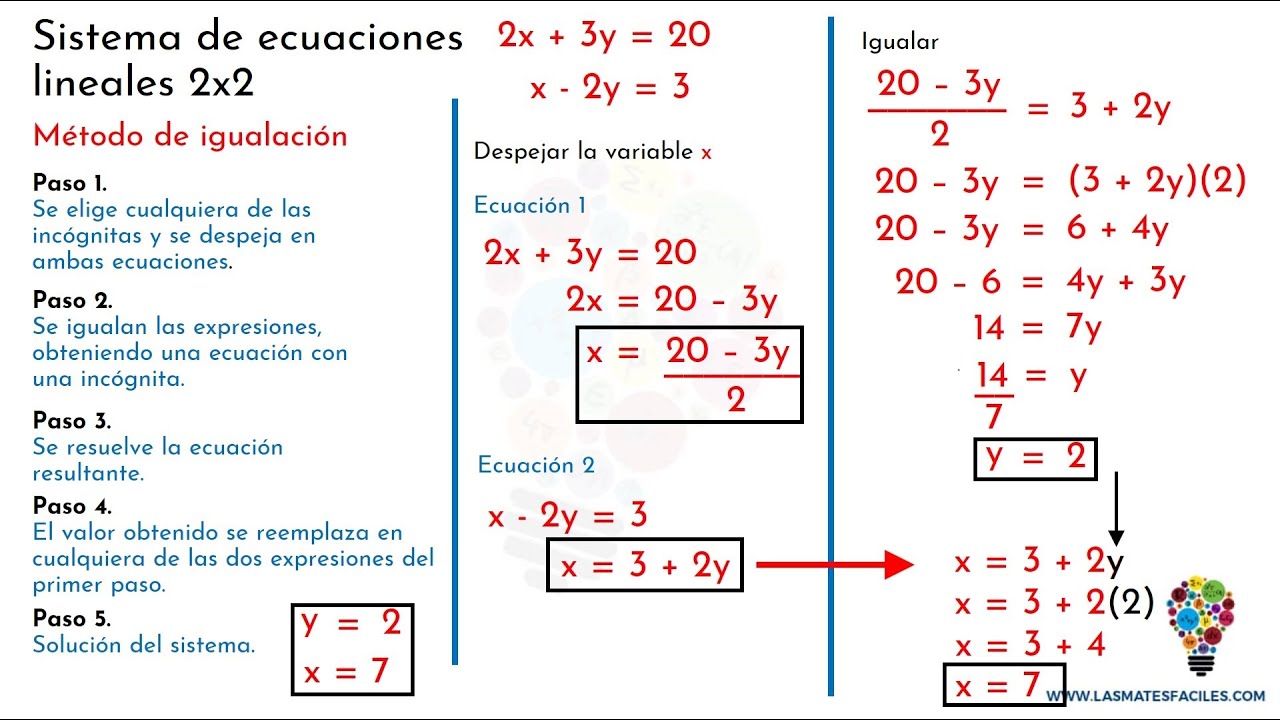
Sistemas de Ecuaciones 2x2 - Método de Igualación

Sistemas de ecuaciones lineales 2x2 INTRODUCCIÓN

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

✅ Sistema de Ecuaciones Lineales [ Método de Eliminación ] - Ejemplos Resueltos #1
5.0 / 5 (0 votes)
