Understanding Young's Modulus
Summary
TLDRThis video introduces Young's modulus, one of the key elastic constants used in engineering to describe how materials deform under load. Through the example of a tensile test, the video explains the relationship between stress and strain and how Young's modulus is determined from the elastic region of the stress-strain curve. It highlights how Young's modulus reflects material stiffness, varies between materials, and is influenced by atomic bonds. The video emphasizes the importance of Young's modulus in material selection for engineering applications, such as ensuring minimal elastic deformation in structures like bridges.
Takeaways
- 📏 Young's modulus is one of the three main elastic constants, alongside shear modulus and bulk modulus.
- 🛠️ It measures how a material deforms under loading, specifically during a tensile test where the material is stretched along its length.
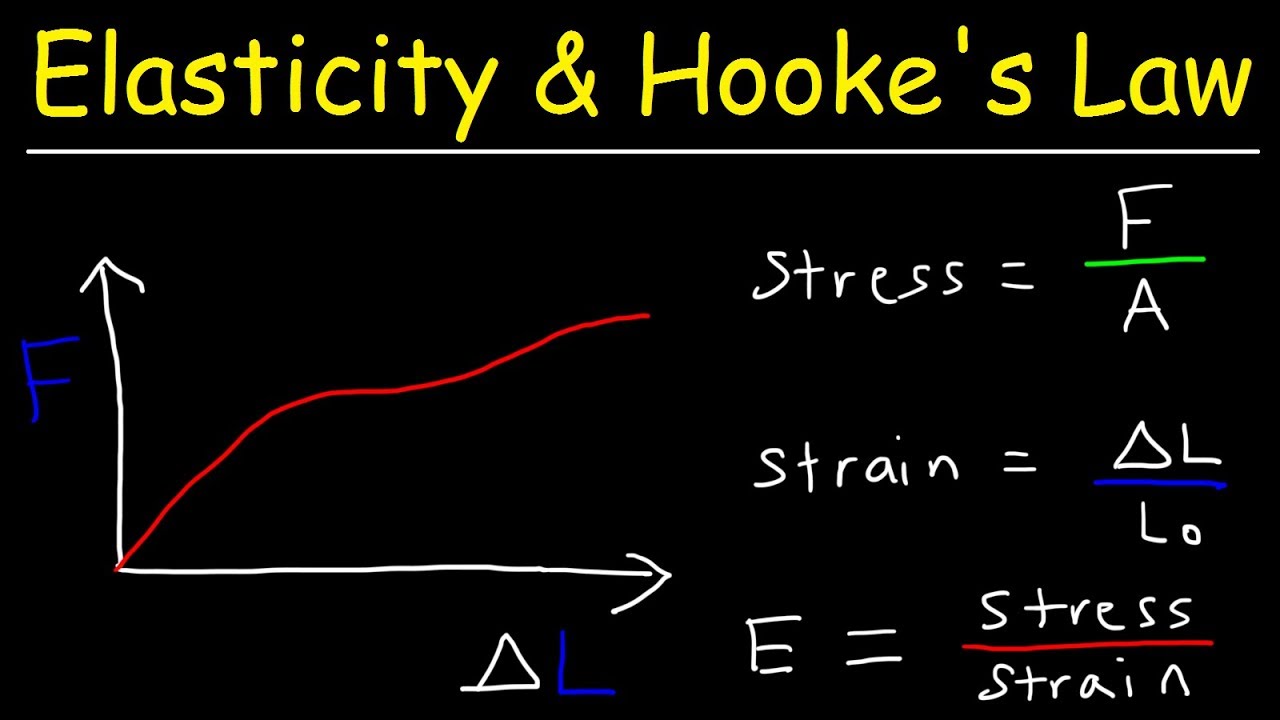
- 📊 The tensile test outputs a stress-strain curve, which shows how a material deforms under different levels of stress.
- 🔄 The stress-strain curve has two main regions: the elastic region (where deformation is reversible) and the plastic region (where deformation is permanent).
- ⚖️ In the elastic region, stress and strain are proportional, and the slope of this linear region represents Young's modulus.
- 🏋️♂️ Young's modulus, denoted as E, is a measure of a material's stiffness—the higher the modulus, the stiffer the material.
- ⚙️ Different materials have different Young's modulus values: ceramics have the highest, metals are lower, and polymers are the lowest.
- 🔬 On the atomic level, Young's modulus is related to the strength of atomic bonds, which act like springs resisting deformation.
- 🧱 Alloyed metals, like mild steel and high carbon steel, have similar Young's modulus values despite differences in other mechanical properties, due to their atomic structure.
- 🏗️ Young's modulus is essential in engineering design, especially when minimizing elastic deformations in structures like bridges.
Q & A
What is Young's modulus and why is it important?
-Young's modulus, also known as the modulus of elasticity, measures the stiffness of a material. It is crucial in engineering design because it helps predict how much a material will deform under a specific load.
How is Young's modulus measured in a tensile test?
-Young's modulus is measured from the slope of the stress-strain curve in the elastic region. It represents the ratio of stress to strain, and its units are the same as stress (Pascals in SI units or psi in US customary units).
What is the difference between elastic and plastic deformation?
-Elastic deformation occurs when the material returns to its original shape after the load is removed. Plastic deformation is permanent, meaning the material does not return to its original dimensions once the load is removed.
What is the significance of the elastic region in a stress-strain curve?
-The elastic region in the stress-strain curve represents the range where the material will return to its original shape after the load is removed. In this region, the relationship between stress and strain is linear, following Hooke's law.
Why do different materials have different values for Young's modulus?
-Different materials have different atomic structures and bonding strengths, which affect how much they deform under stress. For example, ceramics have strong atomic bonds, giving them a higher Young's modulus, while polymers have weaker intermolecular bonds and thus a lower modulus.
How does the direction of load affect Young's modulus in anisotropic materials?
-In anisotropic materials like wood or composites, Young's modulus depends on the direction of the applied load. This is because these materials have different properties in different directions due to their internal structure.
How does Young's modulus relate to atomic bonding in materials?
-Young's modulus is related to the strength of atomic bonds in a material. The elastic strain in a material stretches the inter-atomic bonds, and the stiffness of these bonds determines the material's resistance to deformation.
Why do mild steel and high carbon steel have similar Young's modulus values despite their different mechanical properties?
-Although mild steel and high carbon steel have different mechanical properties, their Young's modulus is similar because the addition of a small amount of carbon atoms doesn't significantly affect the overall resistance of the atomic bonds to elastic deformation.
What role does Young's modulus play in engineering applications, such as bridge design?
-In engineering, Young's modulus is used to select materials that minimize elastic deformation under load. For example, in bridge design, a material with a high Young's modulus is preferred to prevent excessive deflection when heavy loads pass over it.
What are typical Young's modulus values for polymers, metals, and ceramics?
-Ceramics generally have the highest Young's modulus values due to their strong atomic bonds, followed by metals with moderately high values. Polymers have much lower Young's modulus values because of their weaker intermolecular bonds.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Hooke’s Law — Lesson 2

Applications of Elastic Behaviour of Materials | Physics | Class 11

FISIKA KELAS XI | ELASTISITAS DAN HUKUM HOOKE
Elasticity & Hooke's Law - Intro to Young's Modulus, Stress & Strain, Elastic & Proportional Limit

Fisika XI Elastisitas Part 1

Stress, Strain & Young's Modulus | A-level Physics | OCR, AQA, Edexcel
5.0 / 5 (0 votes)
