BENTUK AKAR Kelas 10 Kurikulum Merdeka
Summary
TLDRThis educational video script focuses on the mathematical concept of radicals, exploring the relationship between exponents and roots. It guides viewers through understanding how to convert exponents to radical form, perform algebraic operations like addition, subtraction, and multiplication with radicals, and rationalize radical expressions. The script includes examples to illustrate these concepts, aiming to help students grasp the fundamentals of working with square roots and higher-order roots, emphasizing the importance of recognizing like radicals for algebraic manipulation and the techniques for simplifying radical expressions.
Takeaways
- 📚 The video discusses the relationship between exponents and radicals, aiming to help viewers understand how to convert between the two.
- 🔢 It explains that an exponent a^{m/n} can be rewritten as the radical √[n]{a^m}, emphasizing the placement of the base and the index in the radical expression.
- 📐 The script provides examples to demonstrate how to manipulate radicals, including addition, subtraction, and multiplication, with the condition that like radicals can be combined.
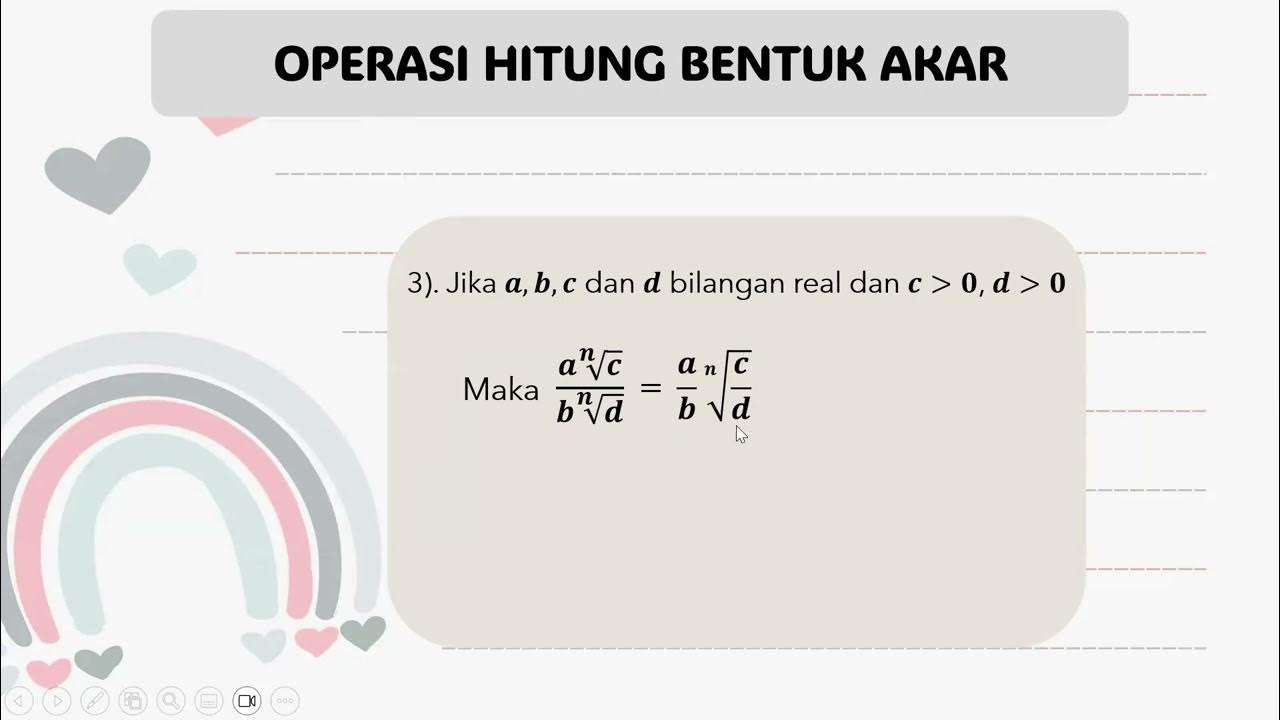
- 🧮 It clarifies that for addition and subtraction of radicals, the index of the radicals must be the same, whereas for multiplication, the index does not need to match.
- 📉 The video shows how to rationalize the denominator of a fraction involving radicals by multiplying the numerator and denominator by the conjugate.
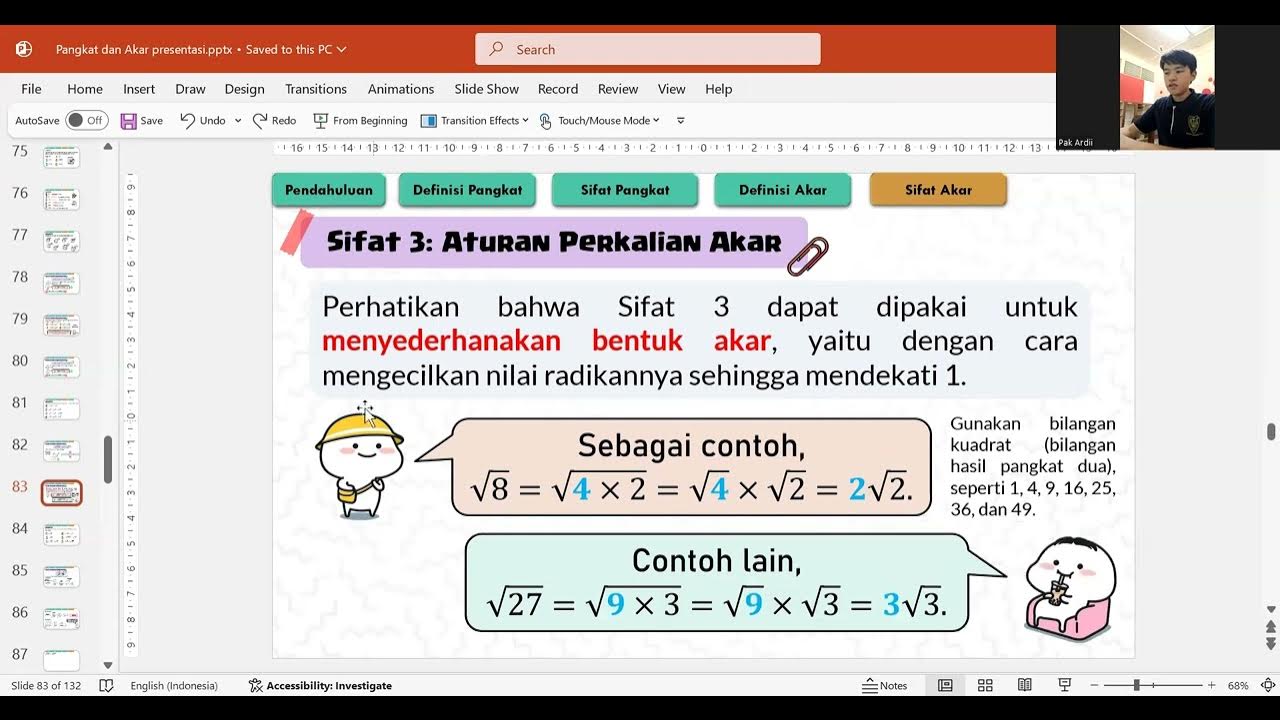
- 📖 It discusses the simplification of radical expressions, including combining like terms and simplifying the expressions under the radical sign.
- 🔄 The script introduces properties of radicals, such as the product of two radicals with the same index being another radical with the same index.
- 📘 It also covers the division of radicals, where the process involves simplifying the expression by taking the radical of the numerator and denominator separately.
- 🔢 The video provides practical examples to illustrate the application of these properties, such as simplifying expressions involving the subtraction of radicals.
- 🤓 The presenter encourages viewers to practice these concepts with problems to solidify their understanding and offers to discuss any questions in class.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the concept of radical expressions, specifically focusing on the relationship between exponents and radicals, operations with radicals, and rationalizing radical expressions.
How can you convert an exponent to a radical?
-You can convert an exponent to a radical by taking the root of the base raised to the power, placing the root index in the denominator and the exponent in the numerator. For example, if you have 'a' raised to the power 'm/n', it becomes the 'n'th root of 'a' raised to the power 'm'.
What is the condition for adding or subtracting radicals?
-Radicals can be added or subtracted only if they are like terms, meaning they have the same radicand and index.
How do you rationalize a radical expression with a radical in the denominator?
-To rationalize a radical expression with a radical in the denominator, you multiply both the numerator and the denominator by the conjugate of the denominator.
What is the process for multiplying radicals?
-When multiplying radicals, you multiply the radicands (the numbers under the radical sign) and keep the index the same. If the radicals are like terms, you can simplify the result further by combining the coefficients.
Can you provide an example of how to simplify a radical expression with a fraction and a radical in the denominator?
-For example, to simplify '2/√5', you multiply the numerator and the denominator by '√5', resulting in '2√5/5'. This process eliminates the radical in the denominator.
What is the rule for dividing two radical expressions?
-When dividing two radical expressions, you divide the radicands and place the result under a single radical sign with the same index.
How do you determine if two radicals are like terms?
-Two radicals are like terms if they have the same radicand and the same index. For example, '√3' and '2√3' are like terms because they both have the same radicand and index.
What is the purpose of rationalizing the denominator in a radical expression?
-The purpose of rationalizing the denominator in a radical expression is to eliminate the radical and simplify the expression to a form that does not have radicals in the denominator, which can make further calculations easier.
Can you explain the process of combining like radical terms?
-To combine like radical terms, you add or subtract the coefficients of the terms while keeping the radical part the same. For example, '3√5 + 2√5' combines to '5√5'.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)