CIRCUNFERENCIA: Centro Fuera del origen. Ecuación Ordinaria y General. FÁCIL. 4 ejemplos
Summary
TLDREl guión del video ofrece una explicación detallada sobre cómo determinar la ecuación de una circunferencia centrada fuera del origen, utilizando la fórmula ordinaria. Se presentan ejemplos gráficos para identificar el centro y el radio, y se muestra el proceso de sustitución y desarrollo de ecuaciones para obtener la forma general. Incluye el cálculo de distancias entre puntos para encontrar el radio y la resolución de binomios al cuadrado. El objetivo es enseñar a los estudiantes a graficar y manipular ecuaciones de circunferencias de manera efectiva.
Takeaways
- 📚 La lección trata sobre cómo determinar la ecuación de una circunferencia centrada fuera del origen utilizando la ecuación ordinaria y general.
- 📐 Para graficar una circunferencia, se necesitan dos datos fundamentales: el centro y el radio.
- 🔍 La ecuación ordinaria de una circunferencia tiene la forma \( (x-h)^2 + (y-k)^2 = r^2 \), donde \( (h, k) \) son las coordenadas del centro y \( r \) es el radio.
- 📝 Al comparar la ecuación dada con la ecuación ordinaria, se identifican las coordenadas del centro y se cambian los signos para adaptarlos a la ecuación.
- 🧭 El radio de la circunferencia se determina como la raíz cuadrada del término independiente en la ecuación.
- 📏 Se pueden utilizar herramientas como un compás para graficar la circunferencia en el plano cartesiano, tomando como referencia el centro y el radio.
- 📉 En el caso de que la ecuación no proporcione directamente el centro y el radio, se pueden leer estos datos de la gráfica proporcionada.
- 🔢 Para determinar la ecuación general de una circunferencia, es necesario desarrollar los términos cuadráticos y combinar los términos intermedios.
- ✂️ Al desarrollar los binomios al cuadrado, se aplican reglas de álgebra como el doble producto y se manejan los signos adecuadamente.
- 📝 La ecuación general de una circunferencia se caracteriza por estar igualada a cero y se presenta ordenada por exponentes decrecientes.
- 📚 Se puede calcular el radio de una circunferencia utilizando la fórmula de distancia entre dos puntos si se conoce el centro y se pasa por otro punto dado.
Q & A
¿Qué es la circunferencia con centro fuera del origen?
-Es una circunferencia cuyo centro no está en el origen del plano cartesiano, sino en alguna otra posición determinada por las coordenadas (h, k).
¿Cuáles son los dos datos básicos necesarios para graficar una circunferencia?
-Los dos datos básicos necesarios para graficar una circunferencia son el centro y el radio.
¿Cómo se representa la ecuación de una circunferencia en forma ordinaria?
-La ecuación de una circunferencia en forma ordinaria se representa como (x-h)^2 + (y-k)^2 = r^2, donde (h, k) son las coordenadas del centro y r es el radio.
¿Cómo se identifican las coordenadas del centro de una circunferencia dada su ecuación ordinaria?
-Las coordenadas del centro de una circunferencia se identifican como h y k, los valores que acompañan a la x y la y dentro del paréntesis en la ecuación ordinaria, respectivamente.
¿Qué es el radio de la circunferencia cuyo valor de r^2 es 16?
-El radio de la circunferencia es la raíz cuadrada de 16, que es 4.
¿Cómo se grafica una circunferencia manualmente si se conoce su centro y radio?
-Para graficar una circunferencia manualmente, se toman 4 cuadritos de referencia arriba, abajo, izquierda y derecha con respecto al centro, para que quede lo más preciso posible.
¿Cómo se determina el radio de una circunferencia si se conoce su centro y se pasa por un punto dado?
-Se utiliza la fórmula de distancia entre dos puntos para calcular el radio, que es la distancia entre el centro de la circunferencia y el punto dado.
¿Qué es la ecuación general de una circunferencia y cómo se obtiene?
-La ecuación general de una circunferencia es la ecuación que resulta después de desarrollar los binomios al cuadrado en la ecuación ordinaria y se caracteriza por estar igualada a cero.
¿Cómo se maneja el signo de las coordenadas del centro al sustituir en la ecuación ordinaria de una circunferencia?
-Al sustituir las coordenadas del centro en la ecuación ordinaria, se cambian los signos de h y k, es decir, si en la ecuación ordinaria están dentro de un paréntesis con signo negativo, en la ecuación general deben tener signo positivo y viceversa.
¿Cómo se calcula la distancia entre dos puntos en un plano cartesiano?
-La distancia entre dos puntos (x1, y1) y (x2, y2) en un plano cartesiano se calcula utilizando la fórmula de distancia: √((x2 - x1)^2 + (y2 - y1)^2).
¿Qué es el término independiente en la ecuación general de una circunferencia y cómo se calcula?
-El término independiente en la ecuación general de una circunferencia es el resultado de sumar los términos que no están elevados al cuadrado ni multiplicados por xy, y se calcula al despejar r^2 en la ecuación ordinaria.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Ecuación de la circunferencia con centro fuera del origen (tercera parte).

CIRCUNFERENCIA: De la ecuación General a la Ordinaria. FÁCIL. 2 ejemplos

Ecuaciones Cuadraticas
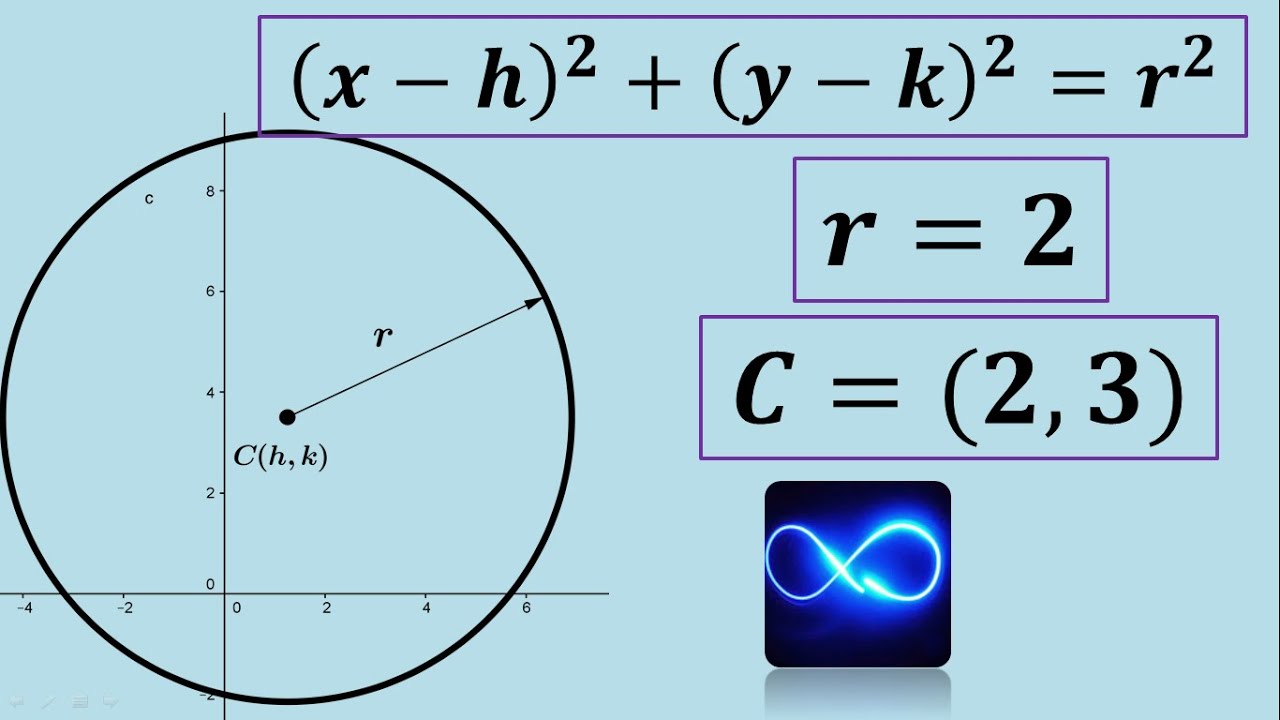
Ordinary and general equation of circumference with given center and radius (Example 1)

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN (En su forma ordinaria)

Ecuación de la circunferencia con centro fuera del origen (cuarta parte)
5.0 / 5 (0 votes)
