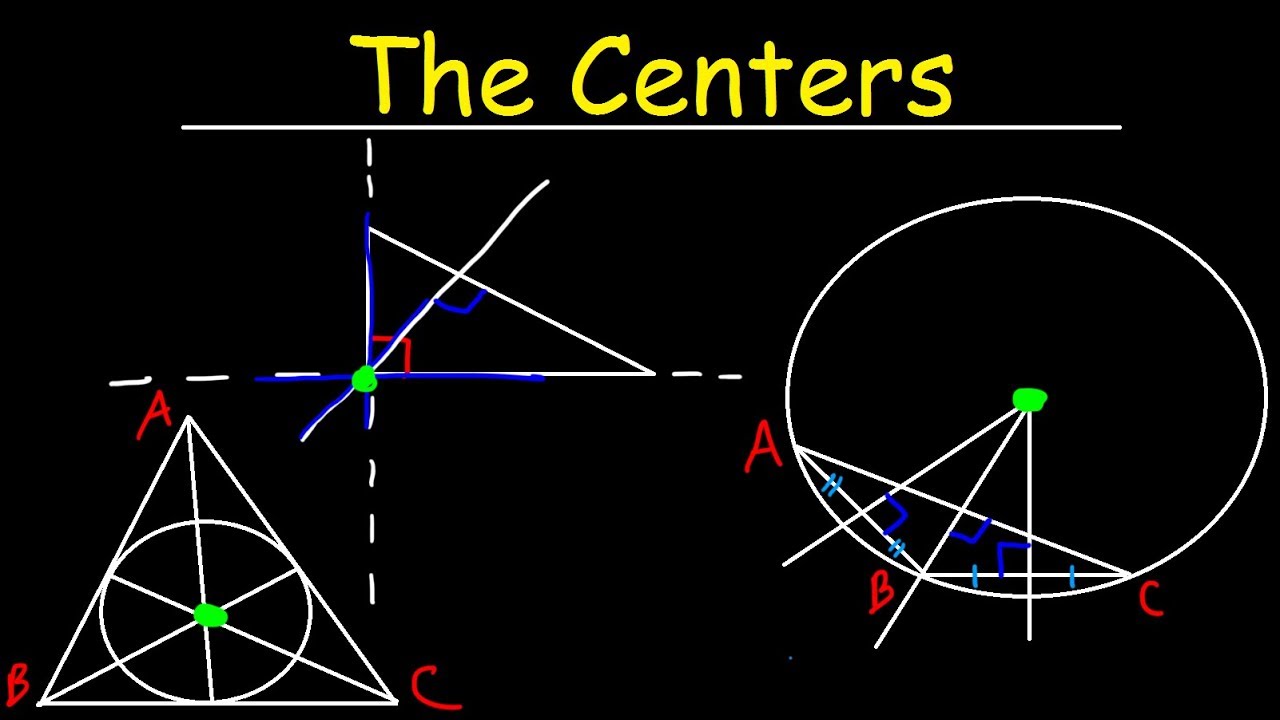
Triangle Centers Identification

Summary

In this episode of 'Math with Sewn,' the focus is on identifying and distinguishing between the various triangle centers: circumcenter, incenter, centroid, and orthocenter. The video explains how each center is determined by specific geometric properties such as perpendicular bisectors, angle bisectors, and medians. It also highlights the congruent relationships that characterize each center. The script provides practical tips for recognizing these centers by examining the angles and sides of triangles, and it includes practice problems to reinforce the concepts discussed.

Takeaways

• 📐 The circumcenter is found by the intersection of the perpendicular bisectors of a triangle's sides.
• 🔄 The circumcenter creates equal angles from the vertices to the center, forming congruent triangles.
• 📏 The incenter is located at the intersection of the angle bisectors, creating congruent segments from the sides to the center.
• 🔺 The centroid is found by the intersection of the medians, which connect the midpoints of the sides to the opposite vertices, and it does not involve 90-degree angles.
• ⚖️ The centroid has a special relationship where the segments from the midpoints to the centroid are proportional to the sides of the triangle.
• 📍 The orthocenter is the intersection of the triangle's altitudes, and it is characterized by 90-degree angles.
• 🔶 The orthocenter does not create congruent triangles and has no proportional relationship between the sides.
• 🧩 To identify the triangle centers, one can draw lines to make 90-degree angles and check if angles or sides are bisected.
• 🔍 Practice problems in the script involve identifying the type of center based on given geometric properties.
• 📚 The script suggests using a reference guide to compare the properties of each center when solving problems.
• 🌟 The video concludes with a reminder to stay positive and look forward to the next episode.

Q & A

What is the circumcenter of a triangle?

The circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect. It is equidistant from all the vertices of the triangle.

How are the perpendicular bisectors related to the circumcenter?

The perpendicular bisectors of the sides of a triangle create equal segments from the center to the midpoints of the sides, and they intersect at the circumcenter.

What is the incenter of a triangle?

The incenter of a triangle is the point where the angle bisectors of the triangle's angles intersect. It is the center of the inscribed circle that is tangent to each side of the triangle.

How does the incenter differ from the circumcenter in terms of congruence?

Unlike the circumcenter, the incenter does not create congruent triangles from the sides or angles. Instead, it is associated with the angle bisectors and the congruence is from the side to the center.

What is the centroid of a triangle?

The centroid of a triangle is the point where the medians intersect. It is also the center of mass or balance point of the triangle.

How is the centroid found in relation to the sides of the triangle?

The centroid is found by drawing medians from each vertex to the midpoint of the opposite side, and the intersection of these medians is the centroid.

What is the orthocenter of a triangle?

The orthocenter of a triangle is the point where the altitudes of the triangle intersect. It is the vertex of the orthic triangle.

Why is the orthocenter sometimes referred to as the 'weird uncle' of triangle centers?

The orthocenter is sometimes called the 'weird uncle' because it does not have as many distinct properties or congruences as the other triangle centers, and it is less commonly discussed.

How can you identify the circumcenter in a problem with given information?

You can identify the circumcenter by looking for the point that is equidistant from the vertices of the triangle, often indicated by perpendicular bisectors or congruent angles to the center.

What is a characteristic of the centroid that helps distinguish it from other triangle centers?

The centroid is characterized by the fact that it does not have any 90-degree angles associated with its construction, unlike the circumcenter and orthocenter.

How can you use the given information in a problem to determine if a point is the incenter?

If the problem indicates that the angles are bisected and the resulting segments are congruent from the side to the center, then the point is likely the incenter.

What is a strategy for solving problems involving the identification of triangle centers?

A strategy is to draw the lines that would create 90-degree angles and then determine whether the sides or angles were bisected, which can help identify the circumcenter, incenter, centroid, or orthocenter.