Matematika Dasar II | Integral Lipat Dua pada Persegi Panjang

Summary

This video explains the concept of double integrals, focusing on their interpretation as volumes under surfaces. It starts by reviewing single-variable integrals, then extends the idea to functions of two variables defined over rectangular domains. The speaker introduces the Riemann sum approach to approximate the double integral and demonstrates its geometric interpretation. Through examples and properties like linearity and domain subdivision, the video helps viewers understand how to calculate double integrals and visualize them as volumes. The concepts are explained step by step, making the topic accessible and engaging for learners.

Takeaways

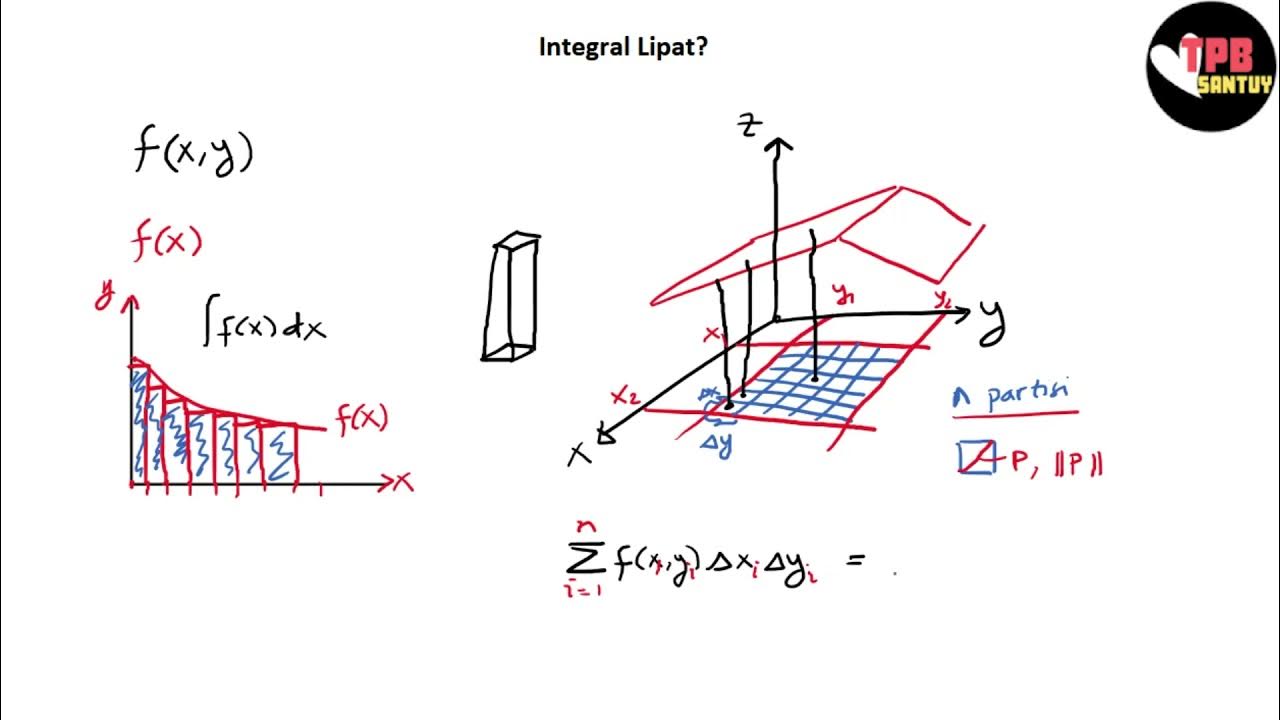
• 😀 The double integral on a rectangular domain is introduced and its concept is explained using the definition of Riemann sums.
• 😀 The area under a curve of a function of one variable can be approximated by using a Riemann sum, which partitions the interval into rectangles.
• 😀 As the partition length approaches zero, the sum of the rectangles becomes a more accurate approximation of the definite integral.
• 😀 A similar approach is applied to functions of two variables, where the double integral represents the volume under the surface defined by the function.
• 😀 The domain for a two-variable function is a rectangle, and partitioning the domain into smaller rectangles helps in approximating the double integral.
• 😀 Each small rectangle in the partition has a base (delta x) and a height corresponding to the function's value at a chosen sample point, typically the midpoint.
• 😀 The sum of volumes of all the small blocks (rectangles) formed by the partition approaches the value of the double integral as the partition becomes finer.
• 😀 The double integral of a function over a rectangular domain can be interpreted as the volume between the surface of the function and the xy-plane.
• 😀 By calculating the double integral, we can find the volume of space between the surface and the domain's base (xy-plane).
• 😀 Properties of double integrals, such as linearity, addition of functions, and the monotonicity property, are discussed and exemplified with practical applications.

Q & A

What is the main concept introduced in the video script?

The main concept introduced in the video is the use of double integrals in a rectangular domain, specifically focusing on how they are related to calculating the volume under a surface, extending the concept of Riemann sums from single-variable to two-variable functions.

What is the connection between the Riemann sum and double integrals?

The Riemann sum is used as an approximation technique for calculating integrals of functions. In the case of a single-variable function, it approximates the area under the curve. Similarly, for a function of two variables, the Riemann sum approximates the volume under the surface by partitioning the rectangular domain into smaller rectangles and summing the volumes of these small blocks.

How does partitioning work in the context of double integrals?

Partitioning involves dividing the rectangular domain into smaller sub-rectangles. The area of each sub-rectangle is determined, and the function's value at a certain point within each rectangle (such as the midpoint) is used to estimate the height of the corresponding block. Summing the volumes of all these blocks gives an approximation of the double integral.

What is the significance of using the midpoint for sample points in the partition?

Using the midpoint of each rectangle for the sample point ensures a more accurate approximation of the function’s value at that point. It represents the average behavior of the function over the small rectangle, leading to a more reliable estimate of the volume when summing the areas of all the blocks.

What is meant by the 'limit' in the context of Riemann sums and double integrals?

The 'limit' refers to the process of refining the partition by making the rectangles smaller and smaller, which results in a more precise approximation of the area or volume. As the partitions approach zero, the Riemann sum converges to the exact value of the double integral.

What is the relationship between the double integral and the volume under the surface?

The double integral of a function of two variables over a rectangular domain represents the volume under the surface defined by the function, between the surface and the x-y plane. It calculates the total volume enclosed by the function over the specified domain.

How can the properties of double integrals, such as linearity and additivity, be used in practice?

The properties of linearity and additivity allow for simplifications when calculating double integrals. For example, a constant factor can be taken out of the integral, and the integral of a sum of functions can be split into the sum of the integrals of each individual function. This helps in breaking down complex integrals into simpler calculations.

What is the purpose of breaking the domain into smaller rectangles when calculating a double integral?

Breaking the domain into smaller rectangles allows for approximating the volume under the surface by calculating the volume of each small block. As the size of these rectangles decreases, the approximation becomes more accurate, and the sum of the volumes of all the blocks converges to the exact value of the double integral.

Why is the function assumed to be continuous for the double integral to be valid?

For the double integral to be valid, the function must be continuous on the rectangular domain, as discontinuities would cause abrupt changes in the function's value, making it impossible to accurately compute the integral. Continuity ensures that the function behaves smoothly over the domain.

Can you explain how a practical example of partitioning and integration might look in the video?

In the example, the rectangular domain is partitioned into smaller square subdomains. For each subdomain, the height is determined by evaluating the function at the midpoint. The area of each small rectangle is calculated, and the volumes of the resulting blocks are summed. This process is repeated for all partitions, and the sum of the volumes approximates the value of the double integral.