Vektor di Bidang Datar Part 1 (Konsep dan Ruang Lingkup) - Matematika Kelas 12

Summary

This video tutorial explains the concept of vectors in mathematics, focusing on their magnitude and direction. It covers the basics of vector representation in everyday life, such as the motion of a car traveling westward at 100 km/h. The video introduces vector notation, including how vectors can be represented with arrows and points, as well as how to calculate their magnitude and direction. Key concepts like equal vectors, negative vectors, position vectors, and zero vectors are discussed. The tutorial also delves into vector operations on the 2D Cartesian plane, using practical examples to demonstrate vector calculations and properties.

Takeaways

• 😀 Vectors are quantities that have both magnitude and direction, such as speed and direction of a moving object like a car.
• 😀 Vectors are represented graphically by arrows, where the length indicates the magnitude and the direction of the arrow represents the vector's direction.
• 😀 The notation for vectors often uses capital letters with arrows above or below them to distinguish them as vectors.
• 😀 Equal vectors have the same magnitude and direction, while negative vectors have the same magnitude but opposite direction.
• 😀 A position vector originates from the origin (0,0) and points to a specific location, and a zero vector has no magnitude or direction.
• 😀 Vectors in a two-dimensional coordinate system (R2) are often written as (x, y), where 'x' is the horizontal component and 'y' is the vertical component.
• 😀 Vector addition and subtraction can be performed by subtracting or adding their respective components (e.g., x2 - x1, y2 - y1).
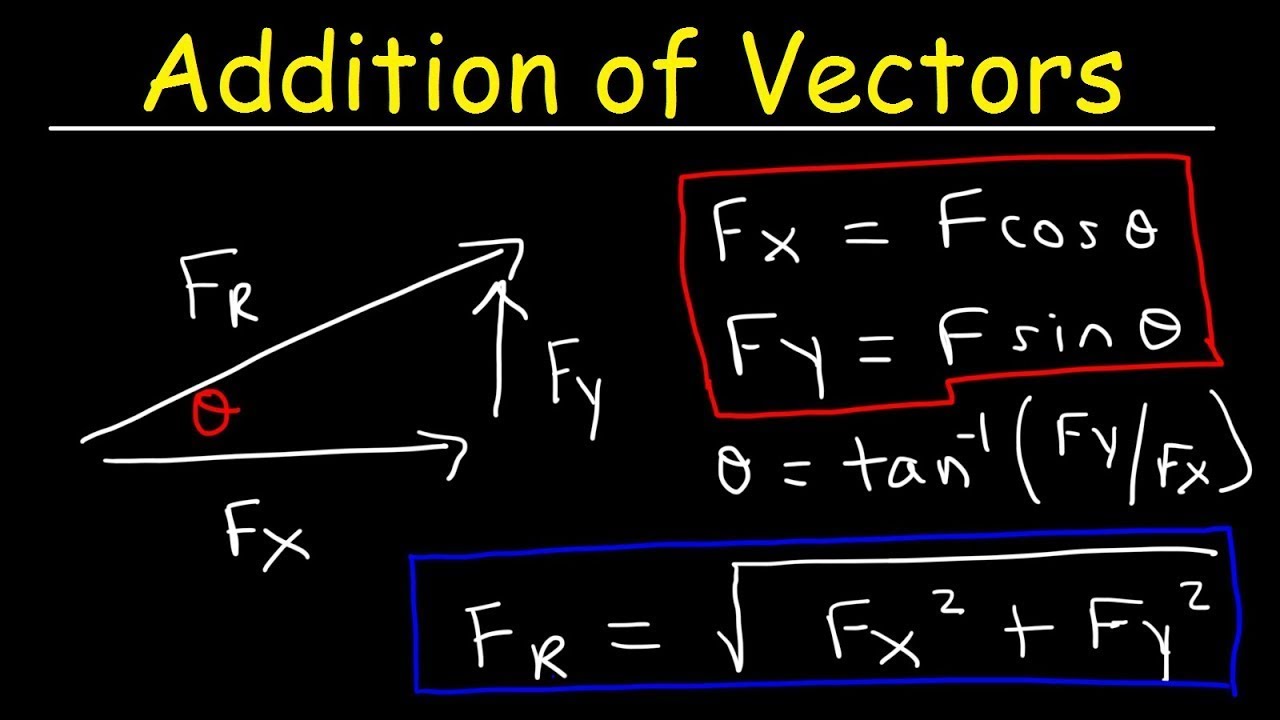
• 😀 The length or magnitude of a vector can be calculated using the Pythagorean theorem: √(x² + y²).
• 😀 Unit vectors are vectors with a magnitude of 1, and they can be derived by dividing a vector by its magnitude.
• 😀 A vector can be used to describe motion or position in real-world situations, such as a car's movement, or an object's position relative to the origin.
• 😀 To calculate the modulus (length) of a vector between two points, you can use the distance formula: √[(x2 - x1)² + (y2 - y1)²].

Q & A

What is a vector?

A vector is a quantity that has both magnitude and direction. It represents physical quantities like velocity, force, and displacement, where both size and direction matter.

How can vectors be represented visually?

Vectors are often represented as arrows, where the length of the arrow indicates the magnitude of the vector, and the direction of the arrow shows the direction of the vector.

What is the significance of the components of a vector?

The components of a vector indicate its projection along specific axes. In a 2D Cartesian coordinate system, these are typically represented as the x and y components, which show how much the vector moves in each direction.

What does it mean for two vectors to be equal?

Two vectors are equal if they have the same magnitude and direction. This means they represent the same physical quantity in both size and orientation.

What is a negative vector?

A negative vector has the same magnitude as its positive counterpart but points in the opposite direction. For example, if a vector represents velocity in one direction, its negative counterpart would represent velocity in the opposite direction.

What is a position vector?

A position vector is a vector that originates at the origin (0,0) of a coordinate system and points to a specific location in space. It indicates the position of a point relative to the origin.

How do you find the vector between two points in a coordinate plane?

The vector between two points A(x1, y1) and B(x2, y2) is calculated by subtracting the coordinates of point A from those of point B. The result is the vector AB = (x2 - x1, y2 - y1).

What is the modulus or magnitude of a vector?

The modulus (or magnitude) of a vector is the length of the vector. In 2D, for a vector represented by coordinates (x, y), its magnitude is calculated using the formula √(x² + y²).

What is a unit vector?

A unit vector is a vector with a magnitude of 1. It indicates direction but has no specific size. To obtain a unit vector from any vector, divide the original vector by its magnitude.

How can we compute the distance between two points using vectors?

The distance between two points A(x1, y1) and B(x2, y2) can be computed using the formula for the magnitude of the vector between them: √((x2 - x1)² + (y2 - y1)²).