Vectors | Trigonometry | Maths | FuseSchool
Summary
TLDRThis educational video explores the concept of vectors, contrasting them with scalars by explaining that vectors have both magnitude and direction. It uses the example of force and velocity to illustrate vector properties and demonstrates how to represent vectors graphically on a coordinate plane. The script also covers vector operations, including addition, subtraction, and scalar multiplication, providing step-by-step explanations and examples to help viewers understand these fundamental principles of vector mathematics.
Takeaways
- 📏 Scalars are physical properties that require only a magnitude, like area, volume, and temperature.
- 🧭 Vectors are physical properties that have both magnitude and direction, such as velocity and acceleration.
- 🔍 A vector is represented by a directed line segment, with a head and a tail, and can be moved without changing its value.
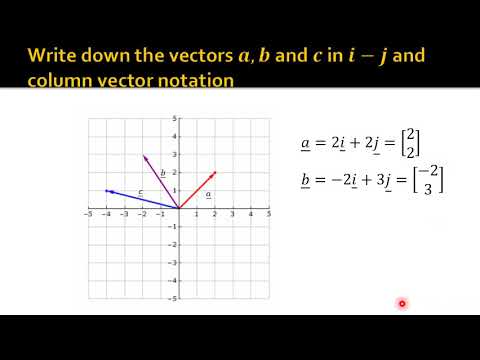
- 📍 Vectors can be placed on a coordinate plane, with the vector's head coordinates representing its magnitude and direction.
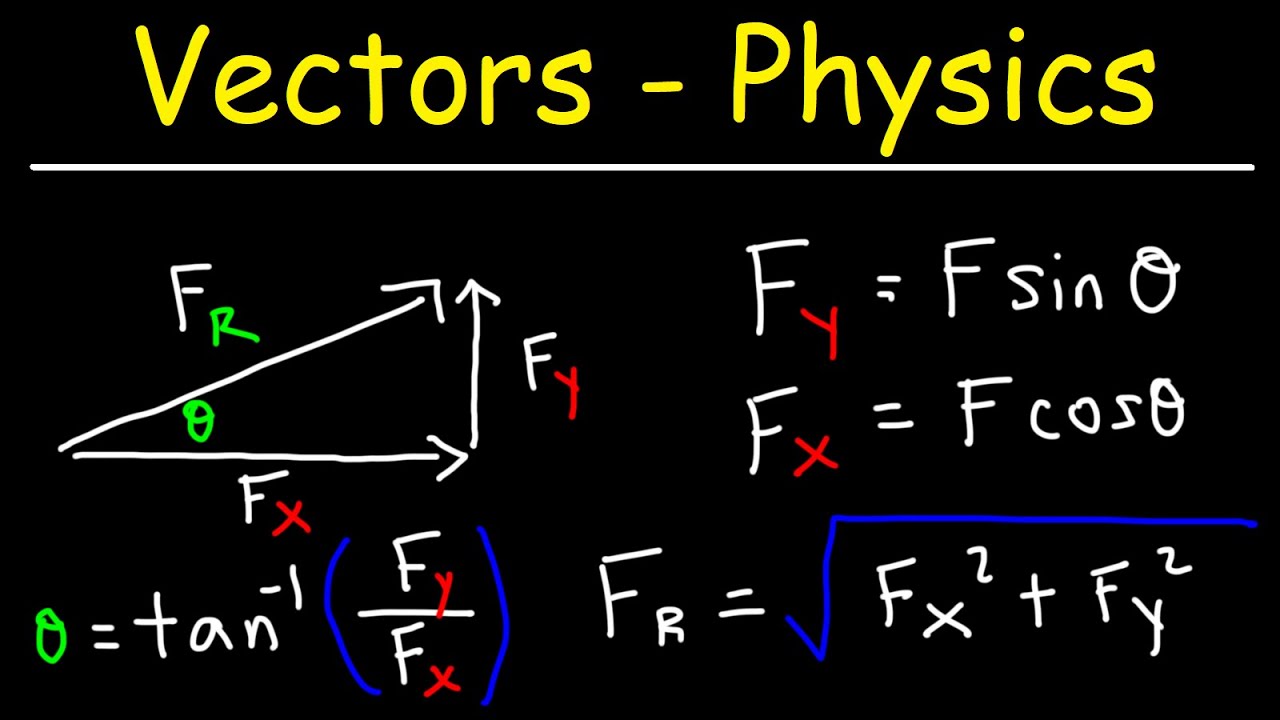
- 📐 The magnitude of a vector can be calculated using the Pythagorean theorem, as the square root of the sum of the squares of its coordinates.
- ➕ Vectors can be added by placing their tails together and drawing a parallelogram, with the diagonal representing the sum.
- 🔢 The sum of two vectors can also be found by adding their corresponding coordinates.
- ✖️ A vector can be multiplied by a number, which scales its magnitude and changes its direction if the number is negative.
- 🔄 To find the difference between two vectors, one vector can be multiplied by -1 and then added to the other.
- 📉 The script provides an example of finding the vector resulting from subtracting 2 times vector b from vector a, and its magnitude.
- 👍 The video encourages interaction by asking viewers to find the coordinates and magnitude of a given vector, and to engage with the content through likes and subscriptions.
Q & A
What is the difference between a scalar and a vector?
-A scalar is a physical property that can be represented by a single number, such as temperature or volume. A vector, on the other hand, has both a magnitude and a direction, such as velocity or force.
Why are vectors important in physics?
-Vectors are important in physics because they allow us to describe physical quantities that have both size and direction, which is crucial for understanding motion, forces, and other phenomena.
What is the magnitude of a vector?
-The magnitude of a vector is its size or length, which can be found using the Pythagorean theorem if the vector is represented in a coordinate system.
How can you represent a vector graphically?
-A vector can be represented graphically as an arrow, where the length of the arrow indicates the magnitude and the direction of the arrow indicates the direction of the vector.
What happens when you add two vectors together?
-When you add two vectors, you can either connect their tails and draw the resultant vector from the first tail to the second head, or place the tails together and form a parallelogram, with the diagonal representing the sum of the vectors.
How do you find the sum of two vectors using their coordinates?
-To find the sum of two vectors using their coordinates, you simply add the corresponding x-coordinates and y-coordinates of the two vectors.
What is the result of multiplying a vector by a number?
-Multiplying a vector by a number scales the magnitude of the vector by that number. If the number is positive, the direction remains the same; if negative, the direction is reversed.
How do you find the difference between two vectors?
-To find the difference between two vectors, you multiply the second vector by -1 to reverse its direction and then add it to the first vector.
What is the significance of the tail and head of a vector in the context of vector addition?
-In vector addition, the tail of the second vector is placed at the head of the first vector, and the resultant vector is drawn from the tail of the first vector to the head of the second.
Can you move a vector without changing its identity?
-Yes, you can move a vector to a different position without changing its identity because a vector's identity is determined by its magnitude and direction, not its position.
What is the formula to calculate the magnitude of a vector given its coordinates (x, y)?
-The magnitude of a vector with coordinates (x, y) can be calculated using the formula: magnitude = √(x² + y²).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)