Exponential Fourier Series Explained | Concept of Negative Frequency Explained
Summary
TLDRIn this video, the concept of the Exponential Fourier Series is explored as an alternative to the Trigonometric Fourier Series. The video explains how periodic signals can be represented by complex exponentials, emphasizing the orthogonality of these complex exponentials and their coefficients. It covers key concepts like signal orthogonality, coefficient calculations, and the relationship between Exponential and Trigonometric Fourier Series. The video also introduces the idea of negative frequencies and explains the importance of the Exponential Fourier Series in understanding Fourier Transforms. Viewers are encouraged to engage with the content through questions or suggestions.
Takeaways
- 😀 The exponential Fourier series represents a periodic signal as a linear combination of complex exponentials.
- 😀 Unlike the Trigonometric Fourier Series which uses sine and cosine waves, the exponential Fourier Series employs complex exponentials.
- 😀 For a signal to be valid in the exponential Fourier Series, the complex exponentials must be orthogonal to each other.
- 😀 Two signals are orthogonal if their integral over a finite time period equals zero, which is proven in the script for the case of complex exponentials.
- 😀 When n equals m in the complex exponential, the integration result is equal to T, showing that the exponentials are orthogonal when n ≠ m.
- 😀 The coefficient Cn in the exponential Fourier Series can be computed by integrating the signal g(t) multiplied by the complex conjugate of the exponential term over one period.
- 😀 If the signal g(t) is real, the coefficients Cn and C-n are complex conjugates of each other, with the same amplitude but opposite phases.
- 😀 The relationship between the exponential and trigonometric Fourier Series coefficients can be derived, with An and Bn related to Cn and C-n.
- 😀 The coefficients Cn and C-n can be expressed in terms of An and Bn, where Cn = (An - jBn)/2 and C-n = (An + jBn)/2.
- 😀 The negative frequencies in the exponential Fourier Series represent the direction of rotation of complex exponentials, but they are still part of the real signal representation.
Q & A
What is the main topic of the video?
-The main topic of the video is the Exponential Fourier Series, which represents a periodic signal as a linear combination of complex exponentials.
How does the Exponential Fourier Series differ from the Trigonometric Fourier Series?
-The Exponential Fourier Series represents a periodic signal as a sum of complex exponentials, whereas the Trigonometric Fourier Series represents it as a sum of sine and cosine functions.
What is the mathematical representation of a periodic signal using the Exponential Fourier Series?
-A periodic signal g(t) with period T can be expressed as a sum of complex exponentials: g(t) = Σ Cn * e^(jnω₀t), where ω₀ = 2π/T and n ranges from -∞ to ∞.
Why are complex exponentials considered orthogonal signals in the context of the Exponential Fourier Series?
-Complex exponentials are orthogonal because their inner product over a period T equals zero when n ≠ m, and equals T when n = m. This orthogonality ensures that each exponential term in the series represents an independent component of the signal.
How is the coefficient Cn of the complex exponentials determined?
-The coefficient Cn is calculated using the formula: Cn = (1/T) * ∫₀ᵀ g(t) * e^(-jnω₀t) dt, where g(t) is the periodic signal and T is its period.
What happens when the signal g(t) is real in terms of the complex conjugate coefficients Cn and C-n?
-When g(t) is real, the coefficients Cn and C-n are complex conjugates of each other, meaning they have the same magnitude but opposite phases.
What is the relationship between the coefficients of the Trigonometric and Exponential Fourier Series?
-The relationship is given by: An = Cn + C-n and Bn = j(Cn - C-n). This allows the coefficients of the Trigonometric Fourier Series to be derived from the Exponential Fourier Series coefficients.
What is the significance of the negative frequency in the Exponential Fourier Series?
-The negative frequency in the Exponential Fourier Series arises from the use of complex exponentials, where e^(jω₀t) represents positive frequency and e^(-jω₀t) represents negative frequency. Both contribute to the representation of the real periodic signal.
Why is the Exponential Fourier Series important for understanding the Fourier Transform?
-The Exponential Fourier Series is crucial for understanding the Fourier Transform because it provides the foundation for analyzing non-periodic signals, which are represented using the Fourier Transform rather than the Fourier Series.
How does the Exponential Fourier Series contribute to the understanding of sinusoidal components of a signal?
-The Exponential Fourier Series decomposes a periodic signal into its sinusoidal components by combining complex exponentials, which are related to sine and cosine terms. This helps in understanding the individual frequency components of the signal.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Introduction to Fourier Series | Trigonometric Fourier Series Explained

FOURIER SERIES LECTURE 1 | STUDY OF DEFINITION AND ALL BASIC POINTS @TIKLESACADEMY
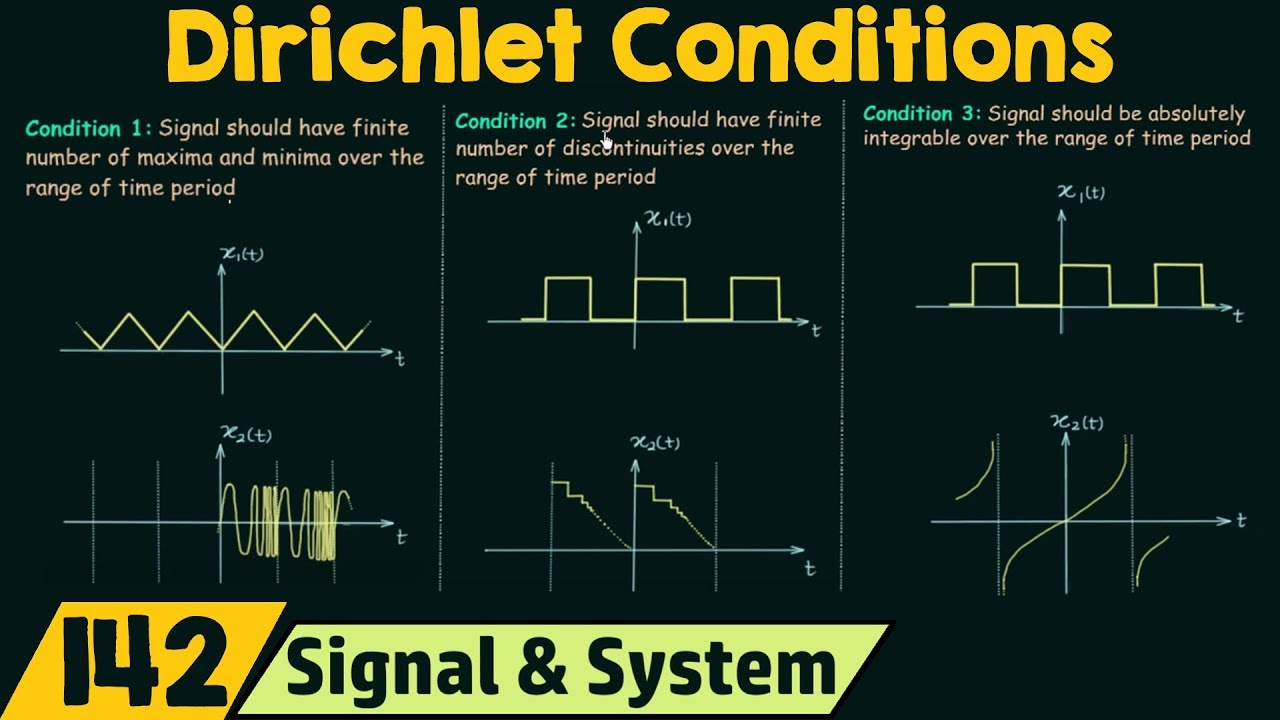
Conditions for Existence of Fourier Series (Dirichlet Conditions)

Intro to FOURIER SERIES: The Big Idea
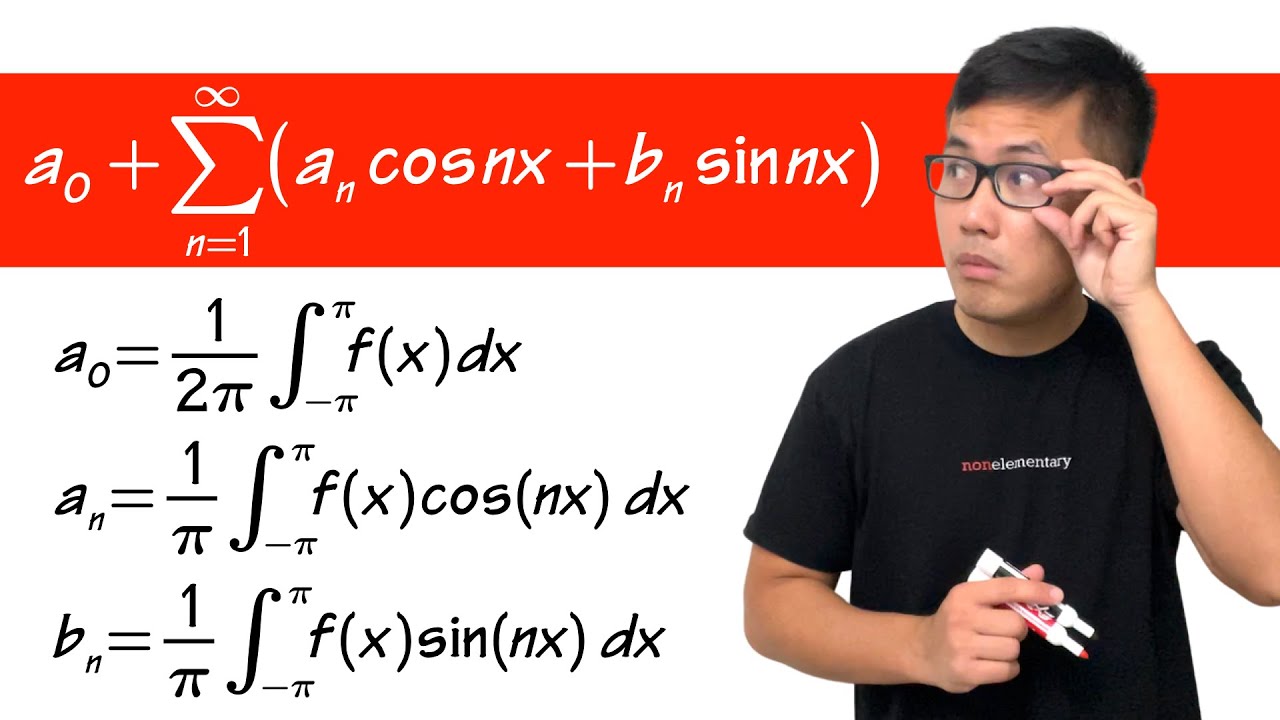
how to get the Fourier series coefficients (fourier series engineering mathematics)

But what is a Fourier series? From heat flow to drawing with circles | DE4
5.0 / 5 (0 votes)
