Konsep Pengukuran Sudut Dalam Lingkaran | Pembahasan Soal SMK

Summary

This video provides an in-depth explanation of the concept of central angles and radians in a circle. It covers the relationship between degrees and radians, using examples to demonstrate conversions such as how 1 radian equals 57.3 degrees. The video also introduces important terms like the radius, arc length, and central angle, explaining how to convert between degrees, minutes, and seconds. With practical examples, the video helps viewers understand the conversion between different angular units, ensuring they grasp the connection between geometry, radian measure, and real-world applications in a circle.

Takeaways

• 😀 The concept of central angles in a circle is explained, where angles are measured from a reference point (e.g., point A) in a clockwise direction.
• 😀 360° represents a full rotation around a circle, with 90° corresponding to a quarter of the circle, 180° to half, and 270° to three-quarters of the circle.
• 😀 The relationship between degrees and radians is highlighted: 360° is equivalent to 2π radians, and 180° is equivalent to π radians.
• 😀 To convert from radians to degrees, multiply the radian value by 180°/π, and to convert from degrees to radians, multiply the degree value by π/180°.
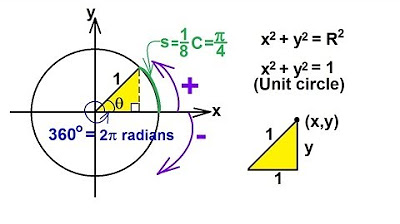
• 😀 One radian is approximately 57.3°, and it occurs when the arc length (the distance along the edge of the circle) is equal to the radius of the circle.
• 😀 The video explains how to convert between degrees, minutes, and seconds, using examples like 35° to 35° 15′ (degrees and minutes).
• 😀 A degree (°) is divided into 60 minutes (′), and each minute is further divided into 60 seconds (″). This system is commonly used for precise angle measurement.
• 😀 To convert a decimal degree like 35.25° to minutes and seconds, the decimal portion (0.25) is multiplied by 60 to give 15 minutes, leaving no remainder in this case.
• 😀 The value of π (approximately 3.14159) is irrational and never ends, though it is often approximated as 22/7 for practical use.
• 😀 The script emphasizes the importance of understanding the relationship between arc length and the angle it subtends at the center of the circle, especially when the arc length equals the radius.

Q & A

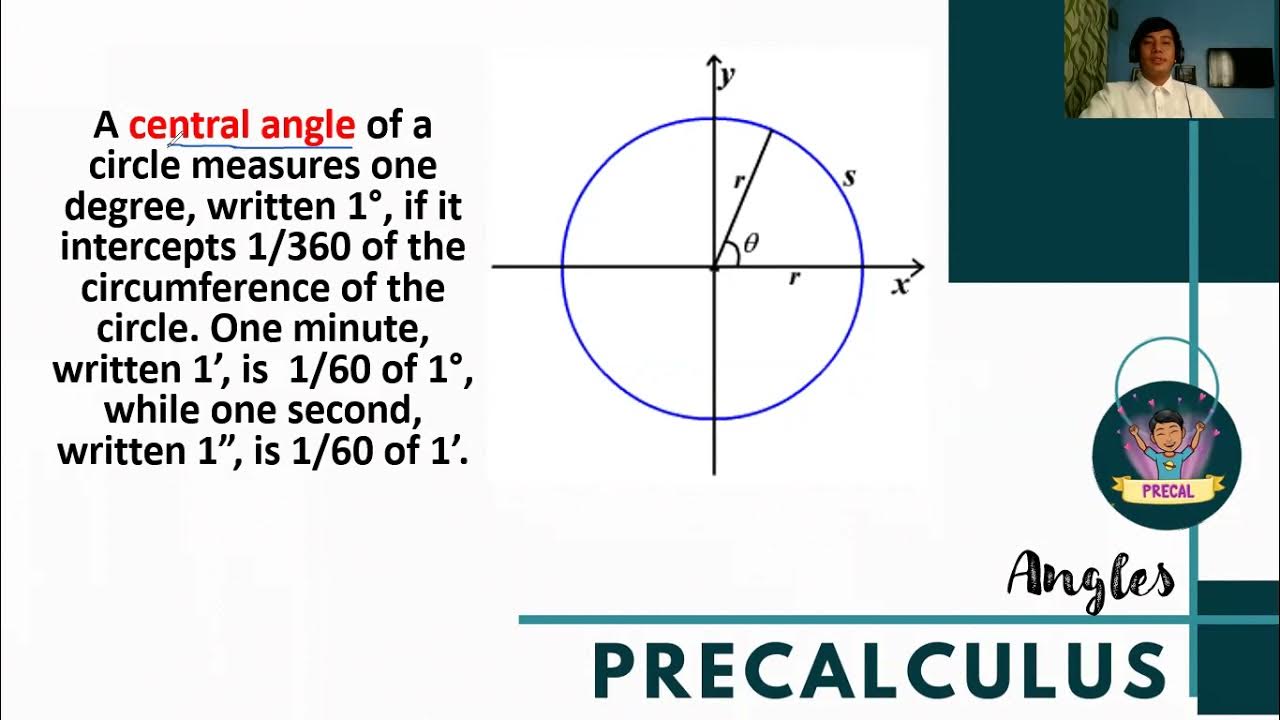
What is the central angle of a circle?

A central angle in a circle is formed when two rays extend from the center of the circle to intersect the circumference. The angle between these two rays is called the central angle.

How is a degree related to the division of a circle?

A full circle is divided into 360 degrees. Each degree represents one part of this total division, and when you move through portions of the circle, the angle swept by the radius is measured in degrees.

What is the relationship between degrees and radians?

The relationship between degrees and radians is based on the fact that 360 degrees equals 2π radians. Therefore, to convert degrees to radians, you multiply by π/180, and to convert radians to degrees, you multiply by 180/π.

What is one radian equivalent to in degrees?

One radian is approximately equal to 57.3 degrees. This occurs when the arc length of a circle equals the radius length.

What is the formula to calculate the circumference of a circle?

The circumference of a circle is calculated using the formula C = 2πr, where r is the radius of the circle.

How can you convert a degree measure into minutes and seconds?

To convert a degree into minutes and seconds, first take the decimal part of the degree and multiply it by 60 to find the minutes. Then, take the decimal part of the minutes and multiply by 60 again to find the seconds.

How do you convert radians to degrees?

To convert radians to degrees, multiply the radian value by 180/π. For example, if you have 3π/2 radians, the equivalent degree measure is 270°.

What is the significance of the number π in angular measurements?

The number π (approximately 3.14159) is fundamental in angular measurements, as it relates the ratio of a circle's circumference to its diameter. It is used to convert between degrees and radians and to calculate the angles in a circle.

What is the difference between a rational and an irrational number in the context of angular measurements?

A rational number, like 22/7, is a fraction that can be expressed exactly, while an irrational number, like π, cannot be expressed exactly as a fraction and has a non-repeating, non-terminating decimal expansion.

How do you convert a time unit, like minutes and seconds, back into a degree measure?

To convert minutes and seconds back into a degree measure, divide the minutes by 60 and the seconds by 3600, then add these to the degree measure. For example, 25° 15' 36'' would be converted as 25 + (15/60) + (36/3600).