StatQuest: t-SNE, Clearly Explained
Summary
TLDRIn diesem Video erklärt der Moderator das Verfahren von T-SNE (t-Distributed Stochastic Neighbor Embedding), einem Verfahren zur Reduktion von hochdimensionalen Datensätzen auf niedrigdimensionalen Raum. Er zeigt, wie T-SNE dabei hilft, Cluster in den Daten zu bewahren, indem es Punkte auf einer eindimensionalen Linie anordnet. Der Prozess umfasst die Berechnung von Ähnlichkeiten zwischen Punkten, die Verwendung einer t-Verteilung zur Skalierung der Ähnlichkeiten und das schrittweise Bewegen der Punkte, um die Ähnlichkeitsmatrix zu optimieren. T-SNE ist besonders nützlich, um komplexe Datensätze zu visualisieren und zu verstehen.
Takeaways
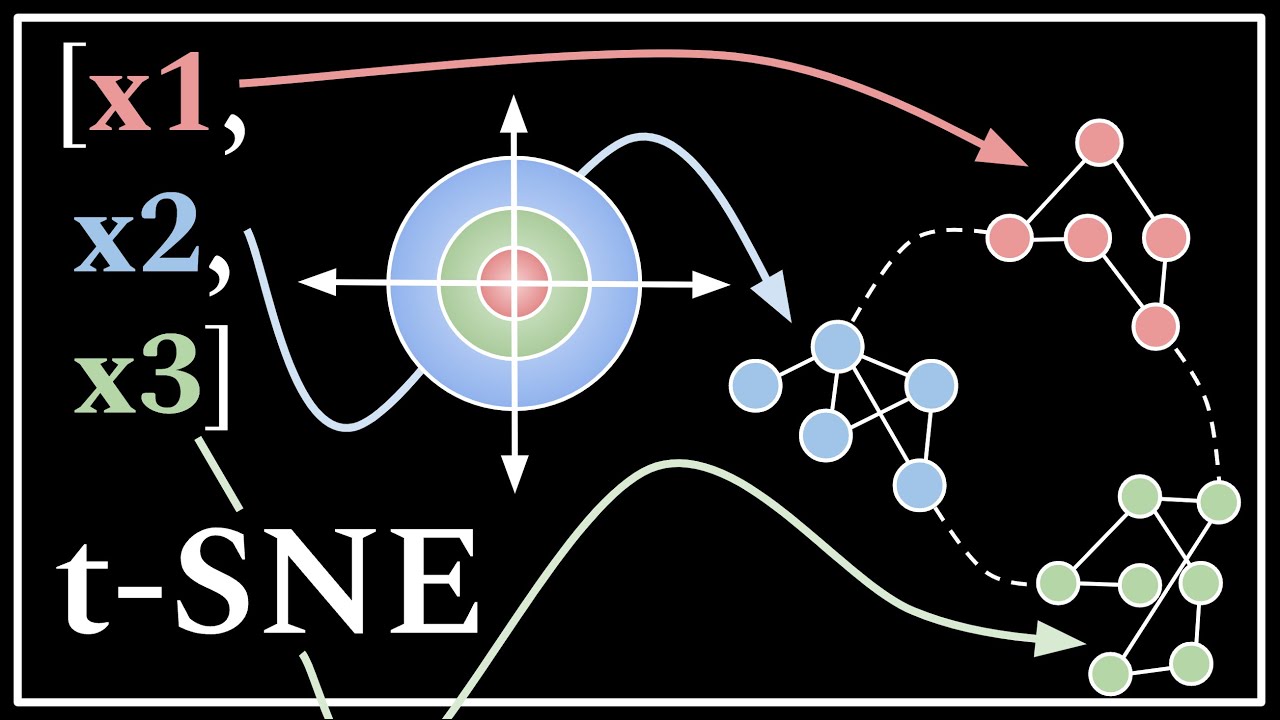
- 😀 T-SNE ist ein Verfahren zur Visualisierung hochdimensionaler Daten in niedrigdimensionalen Räumen, das Cluster und Muster bewahrt.
- 😀 Der Hauptzweck von T-SNE ist es, hochdimensionale Datensätze auf 2D- oder 3D-Grafiken zu reduzieren, um Beziehungen zwischen den Daten sichtbar zu machen.
- 😀 T-SNE berechnet die Ähnlichkeit zwischen den Datenpunkten anhand ihrer Entfernungen im hochdimensionalen Raum und verwendet eine Normalverteilung, um diese Ähnlichkeiten darzustellen.
- 😀 Die Ähnlichkeiten werden skaliert, damit sie auf einer Skala von 0 bis 1 addiert werden, um Dichteunterschiede zwischen Clustern auszugleichen.
- 😀 Eine wichtige Eigenschaft von T-SNE ist die Nutzung der t-Verteilung anstelle der Normalverteilung, um Cluster besser sichtbar zu machen und ein Zusammenklumpen zu verhindern.
- 😀 T-SNE projiziert die Datenpunkte zufällig auf eine Zahlengerade und berechnet dann wieder die Ähnlichkeiten im niedrigdimensionalen Raum.
- 😀 Der Algorithmus optimiert die Positionen der Punkte iterativ, um die Ähnlichkeiten im niedrigdimensionalen Raum mit denen im hochdimensionalen Raum abzugleichen.
- 😀 Die Schritte von T-SNE beinhalten die Berechnung der unskalierten Ähnlichkeit, das Skalieren der Ähnlichkeiten und die Erstellung einer Matrix der Ähnlichkeiten.
- 😀 T-SNE verwendet eine Iterationstechnik, um Schritt für Schritt die Punktpositionen zu ändern, bis die niedrigdimensionale Darstellung den hochdimensionalen Clusterstrukturen entspricht.
- 😀 Am Ende von T-SNE wird eine niedrigdimensionale Darstellung des Datensatzes erzeugt, die dabei hilft, Muster und Beziehungen in den Daten zu erkennen, die ansonsten schwer zugänglich wären.
Q & A
Was ist das Hauptziel von T-SNE?
-T-SNE ist ein Verfahren, das hochdimensionale Datensätze auf eine niedrigdimensionale Graphen-Darstellung reduziert, während es dabei die Struktur und Cluster des ursprünglichen Datensatzes beibehält.
Warum wird T-SNE bei der Visualisierung von Daten verwendet?
-T-SNE hilft dabei, die Komplexität hochdimensionaler Daten zu visualisieren, indem es die Daten in einer niedrigeren Dimension darstellt, was die Muster und Cluster in den Daten hervorhebt.
Was passiert, wenn man die Daten einfach auf eine Achse projiziert?
-Wenn man die Daten einfach auf eine Achse projiziert, geht die ursprüngliche Clusterstruktur verloren, und es entsteht ein unübersichtliches Bild.
Wie funktioniert die Projektion der Daten bei T-SNE?
-T-SNE projiziert die Daten schrittweise auf eine niedrigdimensionale Ebene, wobei es Punkte anzieht, die nahe beieinander liegen, und solche abstößt, die weiter entfernt sind.
Warum sind die Clustereffekte wichtig für T-SNE?
-T-SNE stellt sicher, dass Punkte aus denselben Clustern im hochdimensionalen Raum auch im niedrigdimensionalen Raum zusammen bleiben, was die Visualisierung der Datenstruktur ermöglicht.
Was ist der Unterschied zwischen der normalen und der t-Verteilung?
-Die t-Verteilung hat im Vergleich zur Normalverteilung breitere Enden und eine flachere Spitze. Diese Eigenschaft hilft dabei, die Cluster besser sichtbar zu machen und eine ungewollte Verdichtung in der Mitte zu verhindern.
Warum werden bei T-SNE Ähnlichkeitswerte berechnet?
-Die Berechnung der Ähnlichkeitswerte hilft dabei, festzustellen, wie nahe oder entfernt verschiedene Datenpunkte zueinander stehen, was für das Erhalten der Clusterstruktur im niedrigdimensionalen Raum entscheidend ist.
Was ist die Bedeutung der Perplexitätsparameter bei T-SNE?
-Der Perplexitätsparameter von T-SNE steuert die Dichte der Datenpunkte in der Umgebung eines interessierenden Punktes und hilft dabei, die Breite der Normalverteilung anzupassen.
Was passiert, nachdem die Ähnlichkeitswerte berechnet wurden?
-Nachdem die Ähnlichkeitswerte berechnet wurden, wird die Projektion der Daten auf die niedrigdimensionalen Achsen durchgeführt, wobei die Ähnlichkeitsmatrix schrittweise durch Anpassungen der Punktpositionen optimiert wird.
Warum müssen die Ähnlichkeitswerte für jedes Cluster gleich skaliert werden?
-Die Ähnlichkeitswerte müssen gleich skaliert werden, um sicherzustellen, dass die Dichte von Clustern mit unterschiedlicher Punktdichte miteinander verglichen werden kann, ohne dass dichter gepackte Cluster bevorzugt werden.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
t-SNE Simply Explained

Gelelektrophorese - Aufbau, Prinzip, Ablauf, STR-Methode

Additionsverfahren | lineare Gleichungssysteme | I. + II. | Lehrerschmidt - einfach erklärt!

Haber-Bosch-Verfahren│Chemie Lernvideo [Learning Level Up]

Heron-Verfahren verstehen und anwenden

Método Científico Hipotético Dedutivo de Popper
5.0 / 5 (0 votes)
