Inclined plane force components | Forces and Newton's laws of motion | Physics | Khan Academy

Summary

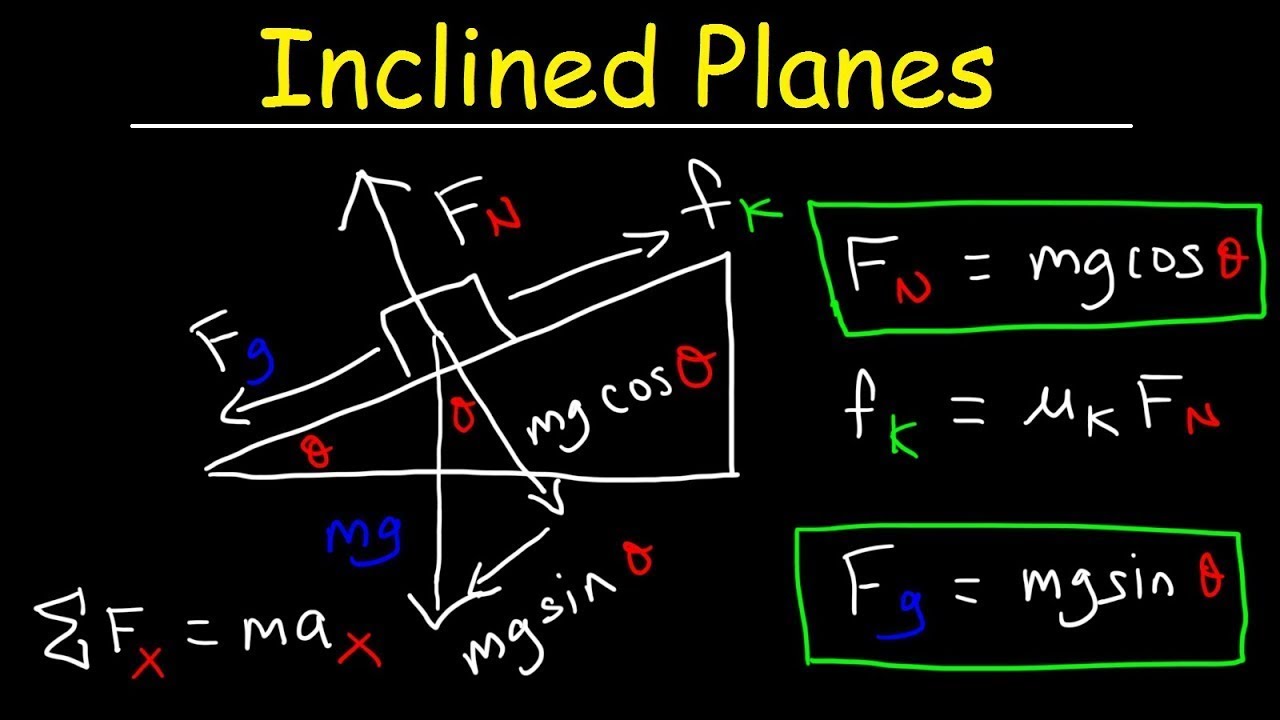
The video script discusses the forces acting on a block with mass 'm' resting on an inclined plane. It introduces the concept of gravity's force pulling the block towards the Earth's center and explains how to break down this force into components: one perpendicular and one parallel to the ramp's surface. Using trigonometry, the script derives the magnitudes of these components in relation to the incline angle 'theta'. The perpendicular component is mg*cos(θ), and the parallel component is mg*sin(θ), where 'g' is the gravitational field near Earth's surface. The explanation aims to help viewers understand how these components can be used to analyze the block's potential motion on the inclined plane, considering normal force and frictional forces.

Takeaways

• 📐 **Gravity Force Decomposition**: The gravitational force acting on a block can be broken down into two components: one perpendicular to the inclined plane (ramp) and one parallel to it.
• 🌐 **Gravitational Field 'g'**: The force due to gravity on an object with mass 'm' is calculated as 'mg', where 'g' is the gravitational field near the Earth's surface.
• 🚫 **Normal Force Clarification**: The normal force acts perpendicular to a surface and is not directly against gravity when the surface is inclined.
• 🔽 **Downward Direction**: The force of gravity is directed downwards or towards the Earth's surface, regardless of the inclined plane's orientation.
• 📐 **Geometry and Trigonometry**: To understand the components of the gravitational force, one must use geometry to decompose the force vector and trigonometry to calculate the magnitudes of the components.
• 📐 **Inclined Plane Angle (θ)**: The angle of the inclined plane is crucial in determining the components of the gravitational force acting on the block.
• 🔄 **Parallel and Perpendicular Forces**: The perpendicular component of gravity is given by 'mg cos(θ)', and the parallel component by 'mg sin(θ)', where 'θ' is the angle of inclination.
• ➡️ **Parallel Force and Motion**: The parallel component of the gravitational force can cause the block to accelerate down the ramp if there is no opposing force, such as friction.
• 🧲 **Normal Force Balancing**: The normal force on the block may counteract the perpendicular component of gravity, keeping the block in place on the inclined plane.
• 🔀 **Force Balancing**: Understanding the balance between the forces acting on the block (gravity, normal force, and possibly friction) is essential for predicting its motion on an inclined plane.
• 📉 **Zero Angle Special Case**: When the inclined plane is horizontal (angle θ = 0 degrees), the perpendicular component of gravity equals the total gravitational force, and the parallel component is zero.

Q & A

What is the mass of the block mentioned in the script?

The mass of the block is represented by the variable 'm'.

What force is acting on the block due to its position near the Earth's surface?

The force acting on the block is gravity, which is represented as the product of the mass 'm' and the gravitational field 'g' near the Earth's surface.

What is the direction of the gravitational force acting on the block?

The gravitational force is acting downwards towards the center of the Earth.

How does the normal force relate to the inclined plane and the force of gravity?

The normal force acts perpendicular to the surface of the inclined plane and is not directly against the force of gravity, which is inclined at an angle theta to the surface.

What are the two components of the gravitational force that the script discusses?

The two components of the gravitational force are the force perpendicular to the ramp (mg cos(theta)) and the force parallel to the ramp (mg sin(theta)).

What is the significance of breaking the gravitational force into components?

Breaking the gravitational force into components allows us to analyze the separate effects of gravity on the block in terms of its potential motion along and perpendicular to the inclined plane.

How does the angle theta relate to the components of the gravitational force?

The angle theta determines the magnitude of the components of the gravitational force. The force perpendicular to the ramp is mg times the cosine of theta, and the force parallel to the ramp is mg times the sine of theta.

What is the role of trigonometry in determining the components of the gravitational force?

Trigonometry, specifically the SOH-CAH-TOA mnemonic, is used to calculate the magnitude of the components of the gravitational force acting on the block parallel and perpendicular to the inclined plane.

What happens if the inclined plane is perfectly horizontal (theta equals 0)?

If the inclined plane is horizontal (theta equals 0), the force of gravity acting parallel to the plane becomes zero (since sine of 0 is 0), and the entire gravitational force acts perpendicular to the plane (cosine of 0 is 1).

What is the term for the force that would counteract the parallel component of gravity if the block is not moving down the plane?

The term for the force that would counteract the parallel component of gravity is the normal force, which acts perpendicular to the surface of the inclined plane.

What might happen to the block if there is no friction and nothing to keep it from moving up the inclined plane?

If there is no friction and nothing to keep the block from moving, the block may start accelerating down the inclined plane due to the parallel component of the gravitational force acting on it.

Outlines

00:00

🌌 Introduction to Forces on an Inclined Plane

This paragraph introduces a scenario where a block with mass 'm' is placed on an inclined plane, or ramp. The focus is on understanding the forces acting on the block, particularly gravity, which pulls the block towards the Earth's center. The gravitational force is denoted by 'mg', where 'g' is the gravitational field near Earth's surface. The paragraph also touches on the concept of breaking down the force of gravity into components parallel and perpendicular to the ramp's surface, which is crucial for analyzing the block's potential motion. Trigonometry and geometry are hinted to be used in future discussions to quantify these forces.

05:00

📐 Analyzing the Components of Gravitational Force

The second paragraph delves into the geometrical and trigonometric analysis of the forces acting on the block. It discusses the concept of the normal force and how it acts perpendicular to the surface, which is not directly against gravity in the case of an inclined plane. The paragraph then explores breaking down the gravitational force into two components using geometry: one perpendicular and one parallel to the ramp. By applying trigonometric principles to a triangle formed by these forces and the ramp's incline at an angle 'theta', the components of the gravitational force are quantified. Specifically, the perpendicular component is 'mg cos(theta)' and the parallel component is 'mg sin(theta)', which are fundamental for understanding how the block may move or remain stationary on the ramp.

10:02

🚀 Understanding the Parallel and Perpendicular Components Intuitively

The final paragraph emphasizes an intuitive understanding of the parallel and perpendicular components of the gravitational force. It suggests a thought process to remember the sine and cosine relationships when the angle of inclination is zero or non-existent. When the ramp is flat (theta equals 0), the perpendicular component of gravity equals the total gravitational force, as all of gravity acts normal to the surface. Conversely, the parallel component would be zero as there is no inclination for the force to act along the plane. This intuitive approach helps in recollecting the trigonometric functions associated with the components of the force due to gravity on an inclined plane.

Keywords

💡Inclined Plane

An inclined plane, also known as a ramp, is a simple machine that allows for the raising of objects by decreasing the effort needed to lift them. In the video, the inclined plane is the surface on which the block is resting, and it is central to the discussion of forces acting on the block. The angle of the inclined plane, denoted as theta, is a key factor in determining the components of gravitational force acting on the block.

💡Mass

Mass (m) is a fundamental property of matter that indicates the amount of matter in an object. In the context of the video, the mass of the block is a crucial parameter in calculating the force of gravity acting upon it. The script mentions that the gravitational force is directly proportional to the mass of the block, which is a fundamental principle in physics.

💡Force of Gravity

The force of gravity is the attractive force that the Earth exerts on objects in its vicinity. It is calculated as the product of the mass of an object and the gravitational field (g) near the Earth's surface. In the video, the force of gravity is broken down into two components: one perpendicular and one parallel to the inclined plane, which is essential for analyzing the block's potential motion.

💡Normal Force

The normal force is the support force exerted by a surface that is perpendicular to the surface itself. It acts to counteract the force of gravity when an object is resting on a surface, such as the inclined plane in the video. The script clarifies that the normal force does not act directly against gravity but is instead perpendicular to the surface of the inclined plane.

💡Components of Force

In physics, forces can be broken down into components that act in different directions. In the video, the force of gravity acting on the block is decomposed into a component perpendicular to the ramp and a component parallel to the ramp. This decomposition is crucial for understanding how the block might move or remain stationary on the inclined plane.

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. In the video, trigonometry is used to calculate the components of the gravitational force acting on the block. Specifically, cosine and sine functions are used to find the perpendicular and parallel components, respectively, based on the angle of inclination (theta).

💡Cosine

The cosine function (cos) from trigonometry is used to find the adjacent side of a right-angled triangle over the hypotenuse. In the context of the video, the cosine of the angle theta is used to calculate the perpendicular component of the gravitational force. It is defined as the force due to gravity times the cosine of theta, which represents the force component acting away from the inclined plane.

💡Sine

The sine function (sin) in trigonometry is used to find the opposite side of a right-angled triangle over the hypotenuse. In the video, the sine of the angle theta is used to determine the parallel component of the gravitational force. This component is responsible for any potential movement of the block along the inclined plane and is calculated as the total gravitational force times the sine of theta.

💡Right Triangle

A right triangle is a triangle that has one angle measuring 90 degrees. In the video, the concept of a right triangle is used to apply trigonometric principles to break down the gravitational force into perpendicular and parallel components. The right triangle formed by the components of the force and the angle of the inclined plane allows for the application of SOH-CAH-TOA to find the magnitudes of these components.

💡Friction

Friction is a force that opposes the relative motion or tendency of such motion of two surfaces in contact. The video briefly mentions friction in the context of what might happen to the block on the inclined plane if there is no friction. Without friction, the parallel component of gravity could cause the block to accelerate down the ramp.

💡Acceleration

Acceleration is the rate of change of velocity of an object with respect to time. In the video, the concept of acceleration is introduced as a possible outcome if the block on the inclined plane is subjected only to the parallel component of gravity and no other forces like friction or a normal force are acting on it. The script suggests that the block might start to accelerate down the ramp under these conditions.

Highlights

The block has a mass m and is subjected to the force of gravity, which can be broken down into components.

The force of gravity (mg) acts towards the center of the Earth.

The inclined plane introduces a need to consider components of the gravitational force parallel and perpendicular to the surface.

The normal force acts perpendicular to the surface and is not directly opposite the gravitational force.

The force of gravity can be decomposed using geometry and trigonometry based on the incline angle theta.

The perpendicular component of gravity is mg times the cosine of theta.

The parallel component of gravity is mg times the sine of theta.

The sum of the angles in a triangle adds up to 180 degrees, which helps in determining the components of force.

The concept of alternate interior angles is used to understand the relationship between angles formed by parallel lines and a transversal.

The angle of inclination of the ramp (theta) is equal to the angle formed between the perpendicular component of gravity and the ramp.

The total gravitational force (mg) is the hypotenuse of the right triangle formed by the force components.

The normal force may counteract the perpendicular component of gravity if the block is not moving down the plane.

In the absence of friction, the block may accelerate due to the parallel component of gravity.

An intuitive understanding of the force components can be gained by considering the case where the incline angle approaches zero.

When the incline angle is zero, all of the gravitational force acts perpendicular to the surface.

The cosine and sine functions describe the magnitude of the perpendicular and parallel components of the gravitational force, respectively.

The mnemonic SOH CAH TOA helps remember the trigonometric relationships in a right triangle.

Transcripts

Let's say I have some type of a block here.

And let's say this block has a mass of m.

So the mass of this block is equal to m.

And it's sitting on this-- you could view this is an inclined

plane, or a ramp, or some type of wedge.

And we want to think about what might happen to this block.

And we'll start thinking about the different forces that

might keep it in place or not keep it in place

and all of the rest.

So the one thing we do know is if this whole set up

is near the surface of the Earth--

and we'll assume that it is for the sake of this video--

that there will be the force of gravity trying

to bring or attract this mass towards the center

of the Earth, and vice versa, the center of the earth

towards this mass.

So we're going to have some force of gravity.

Let me start right at the center of this mass right over here.

And so you're going to have the force of gravity.

The force due to gravity is going

to be equal to the gravitational field

near the surface of the Earth.

And so we'll call that g.

We'll call that g times the mass.

Let me just write it.

The mass times the gravitational field

near the surface of the Earth.

And it's going to be downwards, we

know that, or at least towards the surface of the Earth.

Now, what else is going to be happening here?

Well, it gets a little bit confusing,

because you can't really say that normal force is acting

directly against this force right over here.

Because remember, the normal force

acts perpendicular to a surface.

So over here, the surface is not perpendicular to the force

of gravity.

So we have to think about it a little bit differently than we

do if this was sitting on level ground.

Well, the one thing we can do, and frankly, that we should do,

is maybe we can break up this force,

the force due to gravity.

We can break it up into components

that are either perpendicular to the surface

or that are parallel to the surface.

And then we can use those to figure out

what's likely to happen.

What are potentially the netting forces, or balancing forces,

over here?

So let's see if we can do that.

Let's see if we can break this force vector,

the force due to gravity, into a component that

is perpendicular to the surface of this ramp.

And also another component that is parallel

to the surface of this ramp.

Let me do that in a different color.

That is parallel to the surface of this ramp.

And this is a little bit unconventional notation,

but I'll call this one over here the force due to gravity

that is perpendicular to the ramp.

That little upside down t, I'm saying that's perpendicular.

Because it shows a line that's perpendicular to,

I guess, this bottom line, this horizontal line over there.

And this blue thing over here, I'm

going to call this the part of force

due to gravity that is parallel.

I'm just doing these two upward vertical bars

to show something that is parallel to the surface.

So this is the component of force

due to gravity that's perpendicular, component

of force that is parallel.

So let's see if we can use a little bit

a geometry and trigonometry, given

that this wedge is at a theta degree incline

relative to the horizontal.

If you were to measure this angle right over here,

you would get theta.

So in future videos we'll make it more concrete,

like 30 degrees or 45 degrees or whatever.

But let's just keep in general.

If this is theta, let's figure out

what these components of the gravitational force

are going to be.

Well, we can break out our geometry over here.

This, I'm assuming is a right angle.

And so if this is a right angle, we

know that the sum of the angles in a triangle add up to 180.

So if this angle, and this 90 degrees-- right angle

says 90 degrees-- add up to 180, then that

means that this one and this one need to add up to 90 degrees.

Or, if this is theta, this angle right over here

is going to be 90 minus theta.

Now, the other thing that you may or may not

remember from geometry class is that if I

have two parallel lines, and I have a transversal.

So I'm going to assume this line is parallel to this line.

And then I have a transversal.

So let's say I have a line that goes like this.

We know from basic geometry that this angle

is going to be equal to this angle.

It comes from alternate interior angles.

And we prove it in the geometry module,

or in the geometry videos.

But hopefully this makes a little bit of intuitive sense,

and you could even think about how these angles would

changes as the transversal changes, and all of the rest.

But the parallel lines makes this angle

similar to that angle, or actually makes it identical,

makes it congruent.

This angle is going to be the same measure as that angle.

So can we apply that anywhere over here?

This line is perpendicular to the surface of the Earth.

Right over here that I'm kind of shading in blue.

And so is this force vector.

It is also perpendicular to the surface of the Earth.

So this line over here and this line over here in magenta

are going to be parallel.

I can even draw that.

That line and that line are both parallel.

When you look at it that way, you'll

see that this big line over here can be viewed as a transversal.

Or you could have this angle and this angle

are going to be congruent.

They're going to be alternate interior angles.

So this angle and this angle, by the exact same idea here.

It just looks a little bit more confusing here

because I have all sorts of things.

But this line and this line are parallel.

You can view this right over here as a transversal.

So this and this are congruent angles.

So this is 90 minus theta degrees.

This too will be 90 minus theta degrees.

90 minus theta degrees.

Now, given that, can we figure out this angle?

Well one thing, we're assuming that this yellow force vector

right here is perpendicular to the surface of this plane

or perpendicular to the surface of this ramp.

So that's perpendicular.

This right here is 90 minus theta.

So what is this angle up here going to be equal to?

This angle, let me do it in green.

What is this angle up here going to be equal to?

So this angle plus 90 minus theta plus 90

must be equal to 180, or this angle plus 90 minus theta must

be equal to-- let me write this down.

I don't want to do too much in your head.

So let's call it x.

So x plus 90 minus theta.

Plus this 90 degrees right over here, plus this 90 degrees,

needs to be equal to 180 degrees.

Let's see, we can subtract 180 degrees from both sides.

So we subtract 90 twice, you subtract 180 degrees

and you get x minus theta is equal to 0,

or x is equal to theta.

So whatever the inclination of the plane is or of this ramp,

that is also going to be this angle right over here.

And the value to that is that now we

can use our basic trigonometry to figure out

this component and this component

of the force of gravity.

And to see that a little bit clearer,

let me shift this force vector down over here.

The parallel component, let me shift it over here.

And you can see the perpendicular component

plus the parallel component is equal to the total force

due to gravity.

And you should also see that this is a right triangle

that I have set up over here.

This is parallel to the plane.

This is perpendicular to the plane.

And so we can use basic trigonometry

to figure out the magnitudes of the perpendicular

force due to gravity and the parallel force due to gravity.

Let's think about it a little bit.

I'll do it over here.

The magnitude of the perpendicular

force due to gravity.

Or I should say the component of gravity

that's perpendicular to the ramp, the magnitude

of that vector-- a lot of fancy notation

but it's really just the length of this vector right over here.

So the magnitude of this over the hypotenuse

of this right triangle.

Well, what the hypotenuse of this right triangle?

Well, it's going to be the magnitude

of the total gravitational force.

I guess you could say that.

And so you could say that is mg.

We could write it like this.

But that's really-- well, I could write it like that.

And so this is going to be equal to what?

We have the, if we're looking at this angle right here,

we have the adjacent over the hypotenuse.

Remember.

We can do this in a new color.

We can do this in a new color.

SOH CAH TOA.

Cosine is adjacent over hypotenuse.

So this is equal to cosine of the angle.

So cosine of theta is equal to the adjacent

over the hypotenuse.

So if you multiply both sides by the magnitude

of the hypotenuse, you get the component of our vector that

is perpendicular to the surface of the plane

is equal to the magnitude of the force due to gravity

times the cosine of theta.

Times the cosine of theta.

We'll apply this in the next video

just so you can make the numbers a lot more concrete.

Sometimes just the notation makes it confusing.

You'll see it's really actually pretty straightforward.

And then this second thing, we can use the same logic.

If we think about the parallel vector right over here,

the magnitude of the component of the force

due to gravity that is parallel to the plane

over the magnitude of the force due to gravity--

which is the magnitude of mg-- that

is going to be equal to what?

This is the opposite side to the angle.

So the blue stuff is the opposite side, or at least

its length, is the opposite side of the angle.

And then right over here this magnitude

of mg, that is the hypotenuse.

So you have the opposite over the hypotenuse.

Opposite over hypotenuse.

Sine of an angle is opposite over hypotenuse.

So this is going to be equal to the sine of theta.

This is equal to the sine of theta.

Or you multiply both sides times the magnitude of the force

due to gravity and you get the component

of the force due to gravity that is parallel to the ramp

is going to be the force due to gravity total times

sine of theta.

Times sine of theta.

And hopefully you should see where this came from.

Because if you ever have to derive this again 30 years

after you took a physics class, you should be able to do it.

But if you know this right here, and this right here,

we can all of a sudden start breaking down the forces

into things that are useful to us.

Because we could say, hey, look, this

isn't moving down into this plane.

So maybe there's some normal force

that's completely netting it out in this example.

And maybe if there's nothing to keep it up,

and there's no friction, maybe this thing

will start accelerating due to the parallel force.

And we'll think a lot more about that.

And if you ever forget these, think about them intuitively.

You don't have to go through this whole parallel line

and transversal and all of that.

If this angle went down to 0, then we'll

be talking about essentially a flat surface.

There is no inclination there.

And if this angle goes down to 0, then all of the force

should be acting perpendicular to the surface of the plane.

So if this going to 0, if the perpendicular force

should be the same thing as the total gravitational force.

And that's why it's cosine of theta.

Because cosine of 0 right now is 1.

And so these would equal each other.

And if this is equal to 0, then the parallel component

of gravity should go to 0.

Because gravity will only be acting

downwards, and once again, if sine of theta is 0.

So the force of gravity that is parallel will go to 0.

So if you ever forget, just do that little intuitive thought

process and you'll remember which one is sine

and which one is cosine.