Lingkaran (Bagian 4) - Panjang Busur, Luas Juring & Luas Tembereng | Soal dan Pembahasan SMP MTs
Summary
TLDRThis educational video script focuses on teaching the concepts of arc length, sector area, and ring area in mathematics. It explains how to calculate the arc length using the formula (θ/360) * 2πr and sector area with the formula (θ/360) * πr^2, where θ is the central angle in degrees and r is the radius. The script also covers the calculation of ring area by subtracting the area of a triangle from the sector area. Practical examples are provided to illustrate these concepts, including the use of π ≈ 22/7 for calculations and solving problems involving specific angles and radii. The video aims to help students understand and apply these mathematical formulas effectively.
Takeaways
- 📏 The length of an arc on a circle can be calculated using the formula: (angle / 360) × (circumference), where circumference = 2πr.
- 📐 The area of a sector (juring) is found by the formula: (angle / 360) × (area of the circle), where the area of the circle = πr².
- ➖ To find the area of a segment (tembereng), subtract the area of the triangle from the area of the sector.
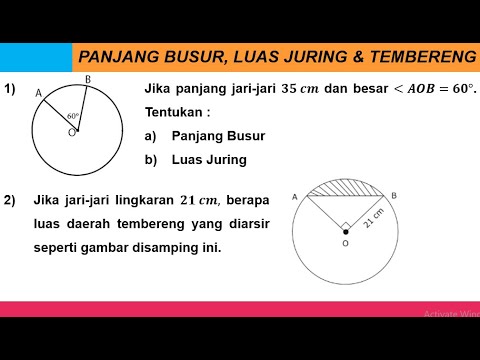
- 🔢 An example problem calculates the arc length using an angle of 108°, with a radius of 5 cm, resulting in an arc length of 9.42 cm.
- 📝 The area of a sector with the same angle (108°) and radius 5 cm is calculated as 23.5 cm².
- 📊 Another example uses a 72° angle and radius of 7 cm to calculate the arc length as 8.8 cm and the sector area as 30.8 cm².
- 🔺 To find the area of a segment in a circle with a right-angled triangle, first find the area of the sector and subtract the triangle's area.
- 🎯 A shortcut formula to calculate the area of a segment can be used, but understanding the core concepts is important for flexible problem-solving.
- 🖋️ A final example shows how to calculate the shaded area in a shape resembling a leaf by using a sector and triangle subtraction approach.
- 🔍 For complex shapes, using the Pythagorean theorem can help find the dimensions needed to calculate areas like segments and sectors.
Q & A
What is the formula to calculate the length of an arc?
-The formula to calculate the length of an arc is given by \( \text{Arc length} = \frac{\theta}{360} \times 2\pi r \), where \( \theta \) is the central angle in degrees and \( r \) is the radius of the circle.
How is the area of a sector calculated?
-The area of a sector is calculated using the formula \( \text{Area of sector} = \frac{\theta}{360} \times \pi r^2 \), where \( \theta \) is the central angle in degrees and \( r \) is the radius of the circle.
What is the difference between the formula for arc length and the formula for the area of a sector?
-The formula for arc length involves multiplying the central angle by the circumference of the circle, while the formula for the area of a sector involves multiplying the central angle by the area of the circle.
How do you find the area of a circular segment?
-The area of a circular segment is found by subtracting the area of the corresponding triangle from the area of the sector. The formula is \( \text{Area of segment} = \text{Area of sector} - \text{Area of triangle} \).
What is the significance of the number 360 in the formulas for arc length and sector area?
-The number 360 signifies the total number of degrees in a circle, and it is used as a denominator to find the fraction of the circle's circumference or area that the arc or sector represents.
How is the circumference of a circle calculated?
-The circumference of a circle is calculated using the formula \( \text{Circumference} = 2\pi r \), where \( r \) is the radius of the circle.
What is the purpose of using the approximation 22/7 for pi in the calculations?
-The approximation 22/7 for pi is used to simplify the calculations when the exact value of pi (approximately 3.14159) is not necessary or when a more precise value is not available.
Can you provide an example of how to calculate the length of an arc given a central angle and radius?
-Sure, if you have a circle with a radius of 5 cm and a central angle of 108°, the length of the arc would be calculated as \( \text{Arc length} = \frac{108}{360} \times 2 \times \frac{22}{7} \times 5 \), which simplifies to approximately 9.42 cm.
How do you calculate the area of a sector if the radius is 7 cm and the central angle is 90°?
-For a sector with a radius of 7 cm and a central angle of 90°, the area is calculated as \( \text{Area of sector} = \frac{90}{360} \times \pi \times 7^2 \), which simplifies to approximately 38.5 square cm.
What is the concept behind the formula for the area of a circular segment?
-The formula for the area of a circular segment is based on the idea that the segment is part of the circle that lies between the chord (the straight line connecting two points on the circle) and the circumference of the circle.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Cara Menghitung Panjang Busur dan Luas Juring Lingkaran

Lingkaran [Part 3] - Panjang Busur dan Luas Juring
Cara Menghitung Panjang Busur, Luas Juring dan Luas Tembereng Pada Lingkaran

12-3 Sector Area and Arc Length
Matematika, Kelas 9, Kurikulum Merdeka, Halaman 91,92,93

Materi Matematika Kelas 8: Lingkaran
5.0 / 5 (0 votes)
