(Part 2) Rotasi Terhadap Titik O (0, 0) Sejauh 90°
Summary
TLDRThis educational video script discusses the concept of rotation around the origin point O (0,0) by 90 degrees, both clockwise and counterclockwise. It provides two formulas for rotating a point with coordinates (x,y) and explains how to find the original point's coordinates given its rotated image. The script includes examples with step-by-step solutions to determine the original coordinates of a point when its rotated image is known. The video encourages viewers to like, comment, subscribe, and share to stay updated and spread knowledge.
Takeaways
- 📚 The video is from Mat Education Official's channel, focusing on learning mathematics.
- 🌟 The topic of the video is rotation around the origin (0,0) by 90 degrees.
- 🔄 Rotating a point (x, y) by 90 degrees clockwise around the origin results in the new coordinates (y, -x).
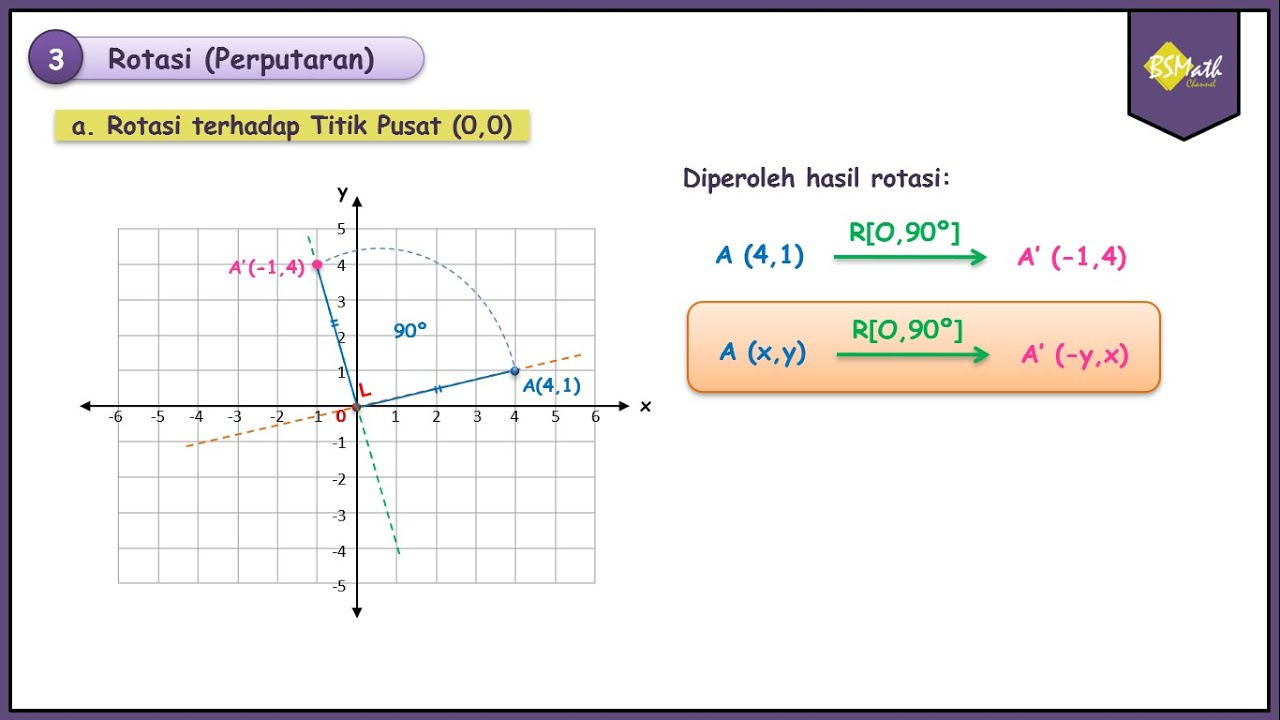
- 🔄 Rotating a point (x, y) by 90 degrees counterclockwise around the origin results in the new coordinates (-y, x).
- 📐 Example 1: To find the original coordinates (x, y) that rotated to (-12, 8) clockwise, the original coordinates are (-8, -12).
- 📐 Example 2: To find the original coordinates (x, y) that rotated to (-10, -6) counterclockwise, the original coordinates are (-6, 10).
- 🔍 The video explains how to find the original point when the image of the point after rotation is given.
- 👍 The video encourages viewers to like, comment, and subscribe to the channel.
- 🔔 Viewers are reminded to turn on notifications to not miss future videos.
- 📢 The video stresses sharing the content to help spread knowledge among friends.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the concept of rotation in mathematics, specifically discussing the rotation of points around the origin by 90 degrees.
What are the two formulas mentioned for rotating a point around the origin by 90 degrees?
-The two formulas mentioned are for rotating a point (x, y) around the origin (0, 0) by 90 degrees in the clockwise direction, resulting in the new coordinates (y, -x), and by 90 degrees in the counterclockwise direction, resulting in the new coordinates (-y, x).
What is the significance of the term 'Alfa' in the script?
-In the script, 'Alfa' refers to the angle of rotation, which is -90 degrees for clockwise rotation and 90 degrees for counterclockwise rotation.
How does the video script introduce the concept of rotation to the audience?
-The script introduces the concept of rotation by explaining the formulas for rotating points around the origin and providing examples of how to determine the original coordinates of a point given its image after rotation.
What are the coordinates of the image of point A after a 90-degree clockwise rotation according to the script?
-The image of point A after a 90-degree clockwise rotation is given as (-12, 8), which means the original coordinates of point A are (-8, -12).
What is the method to find the original coordinates of a point given its image after rotation?
-The method involves using the rotation formulas to set up equations based on the known image coordinates and solving for the original coordinates.
How does the script encourage interaction with the audience?
-The script encourages interaction by asking the audience to like, comment, subscribe, and turn on notifications for the YouTube channel, as well as share the video with friends.
What is the second example problem discussed in the script?
-The second example problem is to determine the original coordinates of point P given its image coordinates after a 90-degree counterclockwise rotation, which are (-10, -6).
What are the original coordinates of point P in the second example problem?
-The original coordinates of point P are (-6, 10), as determined by the rotation formula and the given image coordinates.
How does the script conclude the lesson on rotation?
-The script concludes by summarizing the lesson, encouraging the audience to ask questions if anything is unclear, and ending with a traditional greeting.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

ROTASI (Perputaran) - Cara menentukan bayangan titik di pusat (0,0) dan (a,b)

ASYIK! Rumus ROTASI. TRANSFORMASI FUNGSI. Matematika Kelas 12 [SMA]
Rotasi Terhadap Titik Pusat O(0,0) - Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka
Matematika kelas 9 : Transformasi Geometri (part 3 : Rotasi I)

Transformasi Geometri [Part 3] - Rotasi (Perputaran)

ROTASI (PERPUTARAN) || TRANSFORMASI GEOMETRI
5.0 / 5 (0 votes)
