ROTASI (Perputaran) - Cara menentukan bayangan titik di pusat (0,0) dan (a,b)

Summary

This educational video script focuses on the concept of rotation in mathematics, specifically discussing how to determine the image of a point after rotation. It covers two types of rotations: those centered at the origin (0,0) and those with a center at (a,b). The script explains positive rotation (counterclockwise) and negative rotation (clockwise), providing formulas and examples for calculating the image of a point after a 90° or 270° rotation. The tutorial aims to help viewers easily understand and apply these concepts, with the hope that the material will be beneficial and serve as a valuable learning resource.

Takeaways

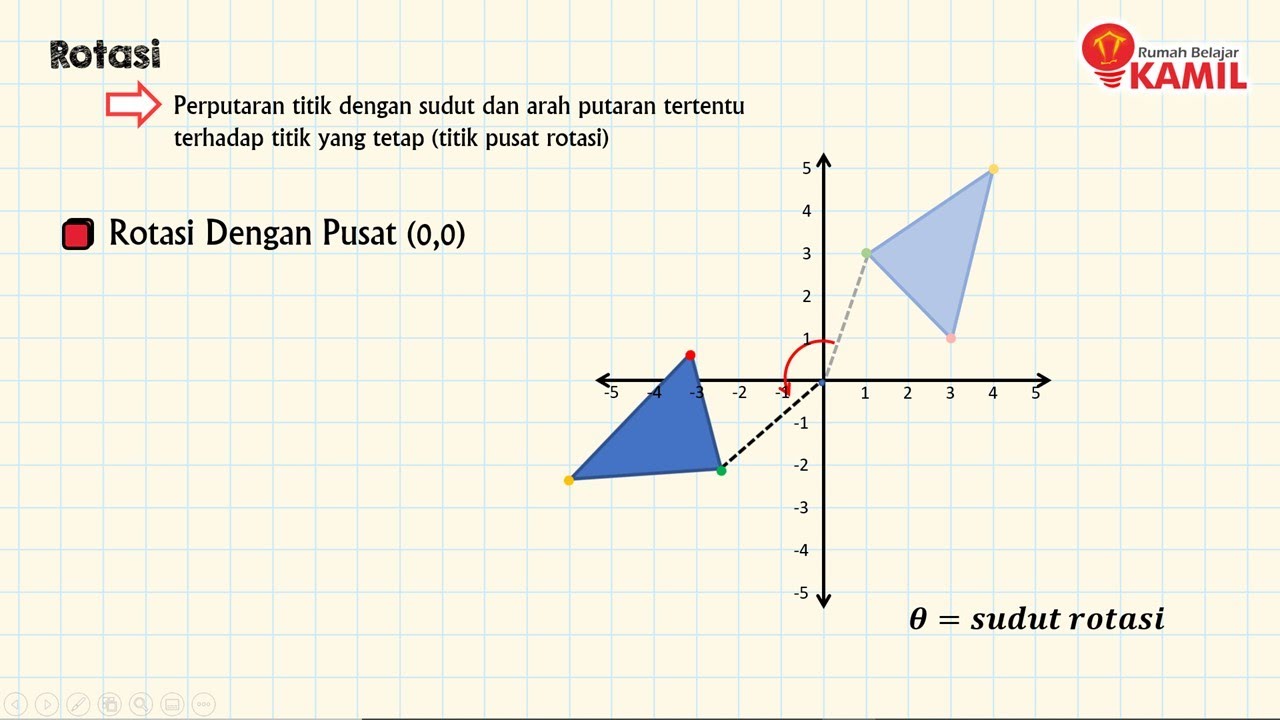
• 📚 The video discusses the concept of rotation in mathematics.
• 🔄 It is divided into two main parts: rotation with the center at (0,0) and rotation with the center at (a,b).
• ⏲️ The first part covers positive rotation (counterclockwise) and negative rotation (clockwise).
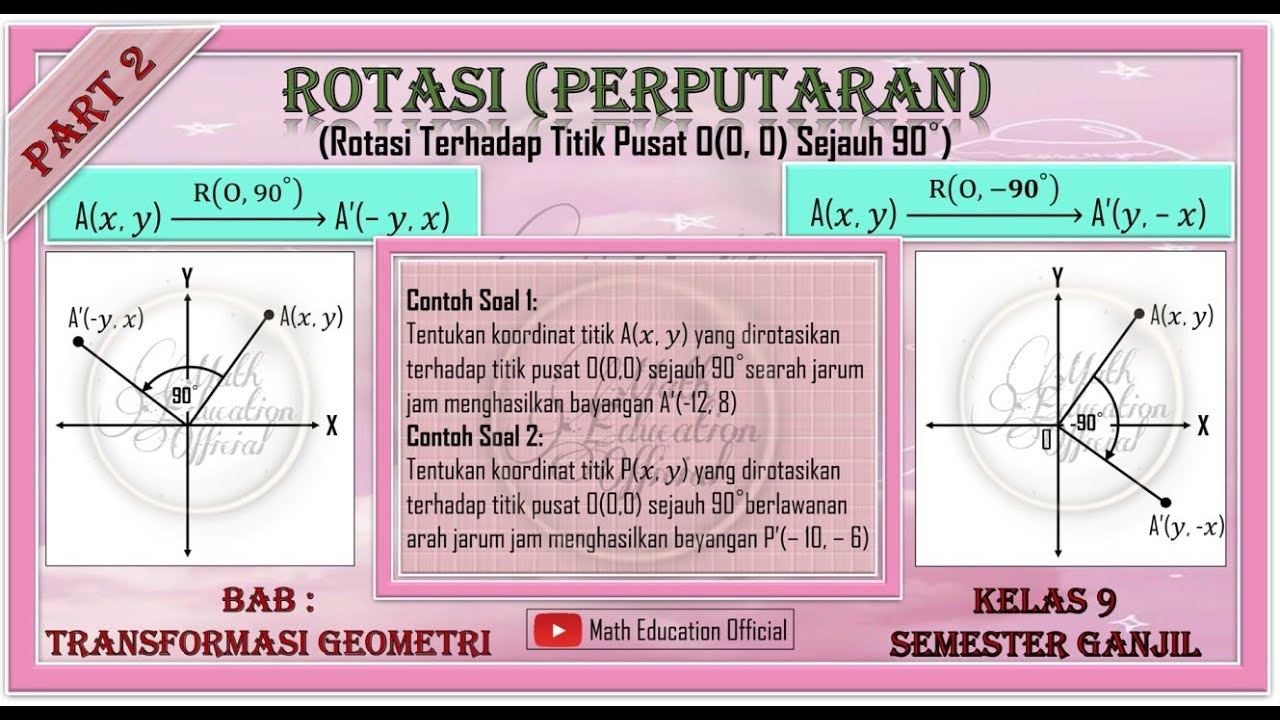
• 📈 For rotation with the center at (0,0), a 90° counterclockwise rotation transforms a point (x,y) to (-y,x), and a 270° clockwise rotation to (y,-x).
• 📐 The second part involves rotation with a center at (a,b), where the formula for determining the image of a point is provided.
• 📝 The video provides a step-by-step guide on how to apply the formula for rotation with a center other than the origin.
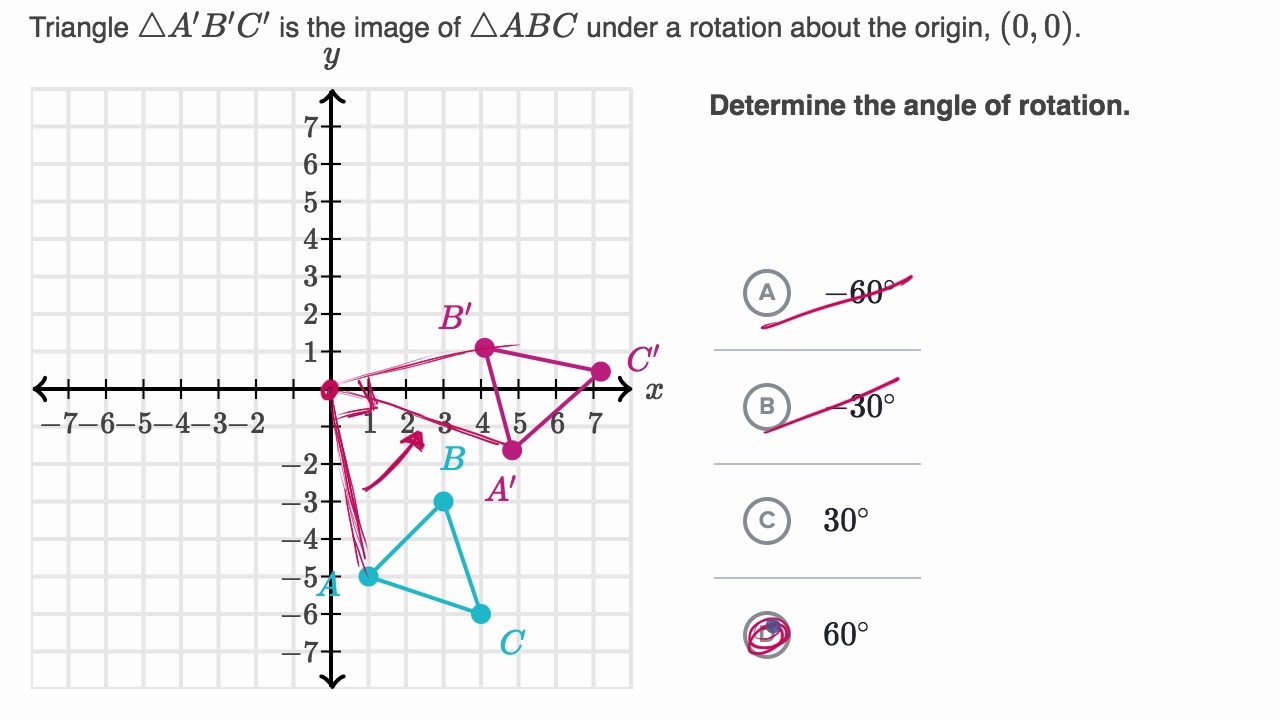
• 📌 An example is given to illustrate how to find the image of point A (3,1) when rotated 90° counterclockwise around the origin.
• 🔢 Another example demonstrates finding the image of point B (-2,-4) when rotated 270° clockwise around the origin.
• 📍 The third example shows how to find the image of point C (3,5) when rotated 90° with the center of rotation at point (1,2).
• 💡 The video emphasizes the importance of understanding and mastering the formulas and tables provided for solving rotation problems.
• 🌐 The tutorial aims to make the concept of rotation easy to understand and apply, with the hope that it will be beneficial for viewers.

Q & A

What is the main topic discussed in the video?

The main topic discussed in the video is the concept of rotation in mathematics, specifically focusing on how to determine the image of a point after rotation.

What are the two types of rotations mentioned in the video?

The two types of rotations mentioned in the video are rotations with a center at the origin (0,0) and rotations with a center at a point (a, b).

What is the difference between positive and negative rotation according to the video?

Positive rotation, also known as clockwise rotation, is when the direction of rotation is opposite to the direction of a clock's hands, while negative rotation, or counterclockwise rotation, is in the same direction as a clock's hands.

How does the video explain the process of finding the image of a point after a 90° clockwise rotation?

The video explains that for a 90° clockwise rotation, the image of a point (x, y) becomes (-y, x), where the x and y coordinates are swapped and the y-coordinate is negated.

What is the formula used to determine the image of a point when rotated around a point (a, b)?

The formula used to determine the image of a point (x, y) when rotated around a point (a, b) is: x' = (x - a) * cos(Alpha) - (y - b) * sin(Alpha) + a, y' = (x - a) * sin(Alpha) + (y - b) * cos(Alpha) + b.

What is the role of the trigonometric functions cos(Alpha) and sin(Alpha) in the rotation formulas?

The trigonometric functions cos(Alpha) and sin(Alpha) are used in the rotation formulas to calculate the new coordinates of the point after rotation, where Alpha represents the angle of rotation.

How does the video demonstrate the process of finding the image of a point after a 270° counterclockwise rotation?

The video demonstrates that for a 270° counterclockwise rotation, the image of a point (x, y) becomes (y, -x), where the x and y coordinates are swapped and the x-coordinate is negated.

What is the significance of the point (a, b) in the context of rotation around a non-origin center?

In the context of rotation around a non-origin center, the point (a, b) represents the center of rotation, and the formulas for finding the image of a point after rotation are adjusted to account for this center.

Can you provide an example of how the video explains the rotation of a point with a specific angle and center?

The video gives an example of rotating point C (3,5) by 90° around the center of rotation P (1,2). The calculations involve using the rotation formulas with the given angle and center coordinates.

What is the final image of point C (3,5) after a 90° rotation around the center P (1,2) according to the video?

After a 90° rotation around the center P (1,2), the image of point C (3,5) is (8,4), as calculated using the provided rotation formulas.

How does the video conclude its tutorial on rotation?

The video concludes by emphasizing the importance of understanding and mastering the rotation formulas, and it ends with a closing remark in Arabic, wishing the viewers well.