Introdução ao Teorema de Pitágoras | Geometria | Khan Academy

Summary

This video explains the Pythagorean theorem, focusing on right triangles and how to use the formula to calculate unknown side lengths. The theorem states that the square of the hypotenuse (the longest side opposite the right angle) is equal to the sum of the squares of the other two sides. Through step-by-step examples, the video demonstrates how to find the hypotenuse or one of the legs of a triangle using this formula. The lesson emphasizes understanding key concepts like the hypotenuse and the application of square roots to solve real-world geometric problems.

Takeaways

• 😀 The Pythagorean theorem is a fundamental concept in geometry and trigonometry, particularly useful for calculating distances between points.
• 😀 To apply the Pythagorean theorem, the triangle must be a right triangle, meaning it has a 90º angle.
• 😀 The longest side of a right triangle, opposite the right angle, is called the hypotenuse.
• 😀 Identifying the hypotenuse involves looking for the side opposite the 90º angle; it is always the longest side.
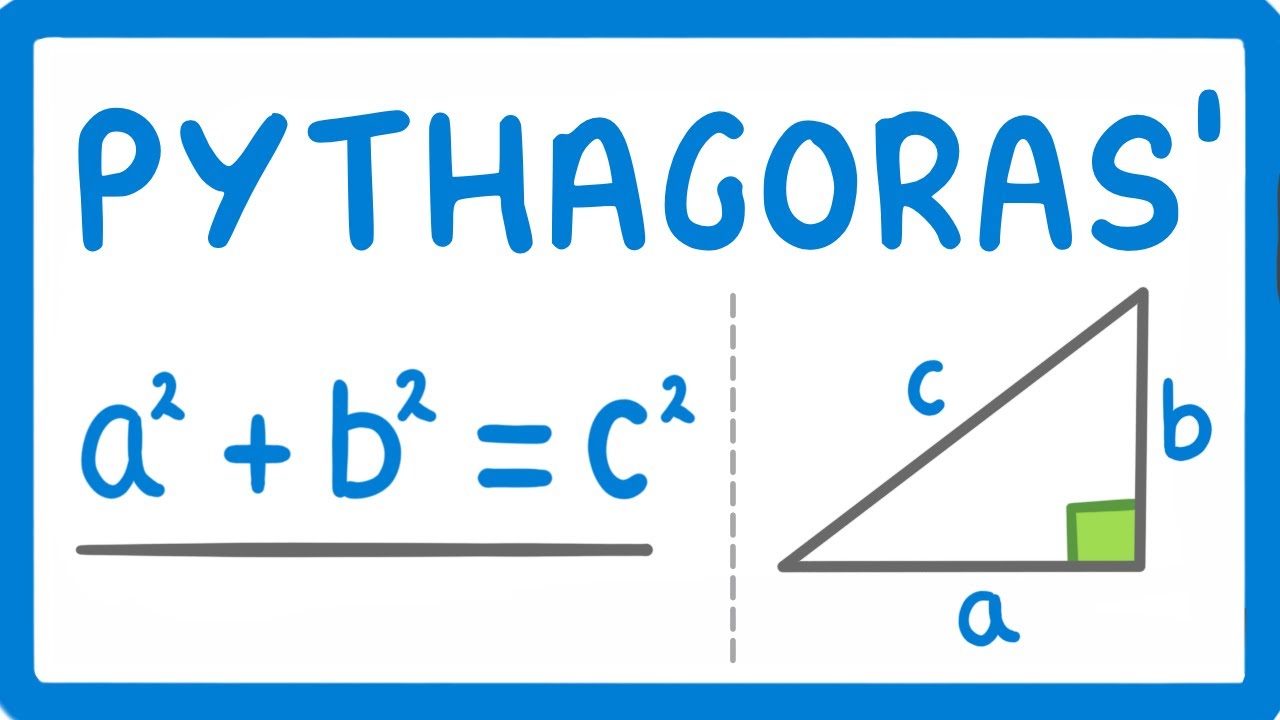
• 😀 The Pythagorean theorem states that the sum of the squares of the two shorter sides equals the square of the hypotenuse: a² + b² = c².
• 😀 For a right triangle with sides 3 and 4, using the Pythagorean theorem, the hypotenuse (c) is 5.
• 😀 When solving for the hypotenuse, square the lengths of the shorter sides, sum them, and then take the square root of the result.
• 😀 The Pythagorean theorem can also be used to find a missing shorter side when the hypotenuse and one other side are known.
• 😀 In one example, given a right triangle with a hypotenuse of 12 and one side of 6, the other side can be found by applying the theorem and simplifying the equation.
• 😀 The square root of 108 simplifies to 6 times the square root of 3, demonstrating the process of simplifying square roots in the context of the Pythagorean theorem.

Q & A

What is the Pythagorean theorem?

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. It is written as: a² + b² = c², where a and b are the lengths of the shorter sides, and c is the hypotenuse.

What is a right triangle?

A right triangle is a triangle that has one angle measuring exactly 90º, which is called a right angle. The longest side of this triangle, opposite the right angle, is called the hypotenuse.

How do you identify the hypotenuse in a right triangle?

The hypotenuse is always the side opposite the right angle, which is the longest side in the right triangle. To identify it, locate the 90º angle and look for the side opposite it.

What are the steps to apply the Pythagorean theorem to find the hypotenuse?

To find the hypotenuse, square the lengths of the two shorter sides of the right triangle, add them together, and then take the square root of the sum. For example, if the sides are 3 and 4, the calculation would be: √(3² + 4²) = √(9 + 16) = √25 = 5.

What is the formula for the Pythagorean theorem?

The formula for the Pythagorean theorem is a² + b² = c², where a and b are the lengths of the two shorter sides of the right triangle, and c is the length of the hypotenuse.

What should you do before applying the Pythagorean theorem?

Before applying the Pythagorean theorem, ensure you can identify the hypotenuse, as this is the side opposite the right angle. Once the hypotenuse is recognized, apply the formula correctly based on what side you are solving for.

How do you solve for the length of a shorter side using the Pythagorean theorem?

To solve for a shorter side, rearrange the Pythagorean theorem formula. For example, if you know the hypotenuse and one side, subtract the square of the known side from the square of the hypotenuse, then take the square root of the result. For instance, if the hypotenuse is 12 and one side is 6, solve as follows: 12² - 6² = 144 - 36 = 108, so the missing side is √108.

How do you simplify square roots when using the Pythagorean theorem?

To simplify square roots, find the prime factorization of the number under the square root. Then, pair up any identical factors. For example, √108 can be factored into √(2² × 3² × 3), simplifying to 6√3.

Why do we ignore negative square roots when applying the Pythagorean theorem?

Since we are dealing with distances in geometry, only positive square roots are considered. Negative values are not practical for measurements of length, so we always take the positive root.

What is the importance of the Pythagorean theorem in real-world applications?

The Pythagorean theorem is crucial in fields like geometry, trigonometry, navigation, and architecture. It helps calculate distances between points, determine angles, and solve problems involving right triangles in various real-world scenarios.