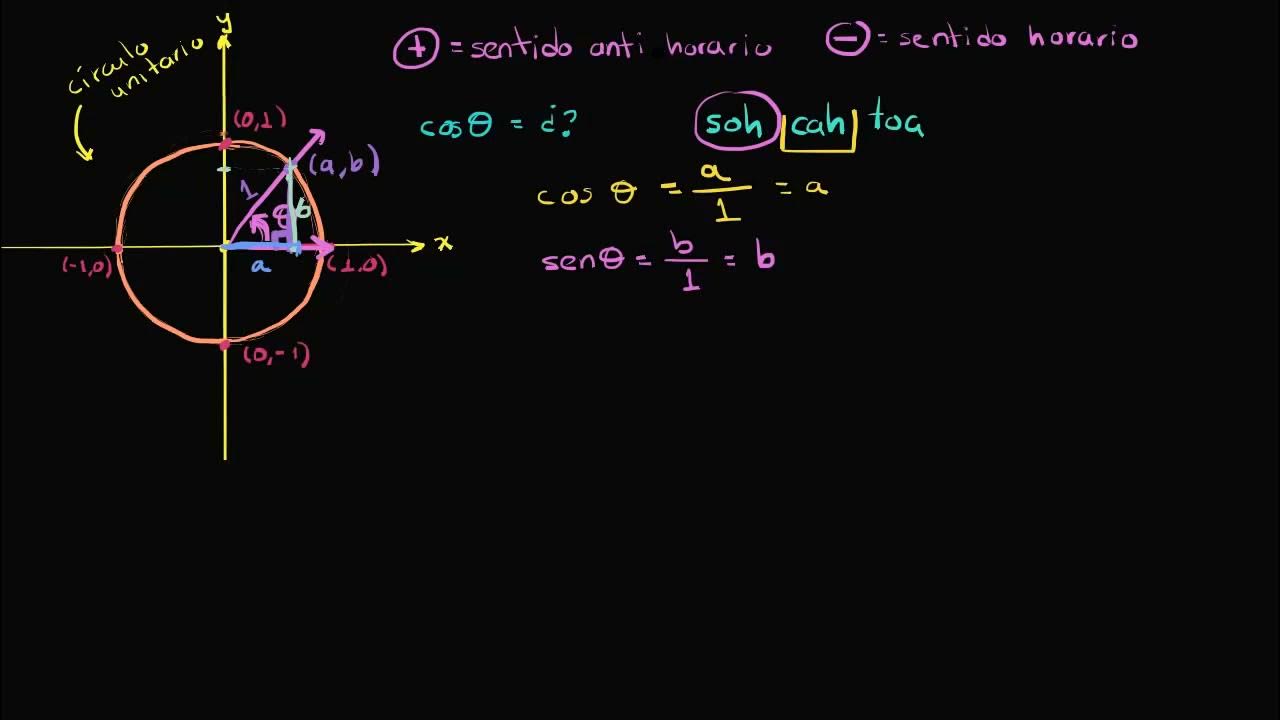Redução à primeira volta

Summary

In this video lesson, the concept of reducing angles to their first revolution in the unit circle is explored. The instructor covers key ideas such as full rotations (2π radians), positive and negative angles, and how to handle fractions of rotations. Examples show how to reduce angles greater than 2π by determining how many full rotations fit within the given angle and handling negative angles with a clockwise direction. Additionally, the lesson includes methods for working with fractional angles, breaking them into smaller, understandable components, and associating them with specific points on the unit circle for clarity.

Takeaways

• 😀 The video discusses the concept of reduction to the first revolution in the context of trigonometric circles.
• 😀 A unit circle is described as a circle with radius 1, with a positive (counterclockwise) and negative (clockwise) direction for measuring angles.
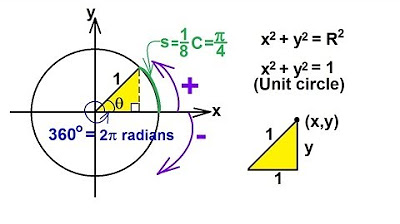
• 😀 The concept of multiple revolutions is introduced, where after completing one full revolution (2π radians), one returns to the same point on the circle.
• 😀 The general form for describing arcs in the unit circle is expressed as n full revolutions (n × 2π radians) plus some additional angle.
• 😀 The video provides examples of how to determine where an angle ends after several full revolutions.
• 😀 In the first example, an angle of 11π is decomposed into 5 full revolutions (5 × 2π) plus an additional π radians.
• 😀 A second example discusses negative angles, such as -5π, where the angle is measured in the clockwise direction.
• 😀 The video explains the process of determining how many full revolutions fit into a given angle, both positive and negative.
• 😀 The importance of using integer multiples of 2π for full revolutions is emphasized, as fractional multiples result in incomplete revolutions.
• 😀 The concept of fractional angles is introduced with an example of 25π/3, demonstrating how to extract the integer part and handle the remaining fraction.
• 😀 The script also covers negative fractional angles, using the example of -19π/6, and explains how to break it into multiple revolutions and partial rotations.
• 😀 Different methods are presented for working with fractional angles, including considering full revolutions and smaller portions (e.g., fractions of a quadrant).

Q & A

What is the concept of the unit circle in trigonometry?

The unit circle is a circle with a radius of 1 centered at the origin. It is used to define trigonometric functions like sine and cosine based on the coordinates of points on the circle corresponding to various angles.

What is the direction of positive angles on the unit circle?

Positive angles are measured in the counterclockwise direction, which is the standard convention on the unit circle.

What happens when an angle completes multiple rotations around the unit circle?

After completing one full rotation, the angle returns to the same point. This means that if an angle is more than a full rotation, it can be reduced by subtracting full rotations (multiples of 2π radians) to find an equivalent angle.

How can we reduce an angle greater than 2π radians?

To reduce an angle greater than 2π radians, we divide the angle by 2π to determine how many full rotations it represents, then subtract the corresponding number of full rotations to obtain an equivalent angle within one full rotation.

What is the significance of the number of full rotations when reducing angles?

The number of full rotations (in terms of 2π radians) helps to understand how many complete turns the angle makes. By subtracting these full rotations, we can find the remainder, which represents the equivalent smaller angle within one rotation.

How do negative angles behave on the unit circle?

Negative angles are measured in the clockwise direction on the unit circle. This means that a negative angle indicates a movement in the opposite direction compared to positive angles.

How can we handle negative angles when reducing them?

For negative angles, we follow the same approach as with positive angles by determining how many full negative rotations (in multiples of -2π radians) fit into the angle and then subtracting those full rotations to find an equivalent angle within one full rotation.

What happens when we encounter a fraction in the angle, like 25π/3?

When dealing with fractions like 25π/3, we can extract the integer part of the fraction by dividing the numerator by the denominator. The quotient gives the number of full rotations, and the remainder is the fractional part that will be used to find the reduced angle.

How do we interpret fractions like π/3 in the context of the unit circle?

Fractions like π/3 represent a fraction of a full rotation. Specifically, π/3 corresponds to 60 degrees, or one-third of a full rotation (360 degrees). This means the angle represents a segment of the unit circle that is 60 degrees long.

What is the importance of understanding the division of the unit circle into smaller parts?

Dividing the unit circle into smaller parts, such as quarters, thirds, and sixths, helps us understand specific angle measures like 30°, 60°, or 90°. These divisions provide a way to break down complex angles into simpler, more manageable components, aiding in calculations and visualizations.