Merge sort in 3 minutes
Summary
TLDRIn this video, viewers are introduced to the merge sort algorithm, focusing on the divide-and-conquer approach. The process involves recursively splitting an array into smaller subarrays until each item is individual. These smaller arrays are then merged back together in sorted order. The video walks through each step in detail, explaining how merging works and highlighting the time complexity of merge sort, which is O(n log n). The video concludes with pseudocode and an easy-to-understand explanation of how recursion and merging play crucial roles in sorting an array efficiently.
Takeaways
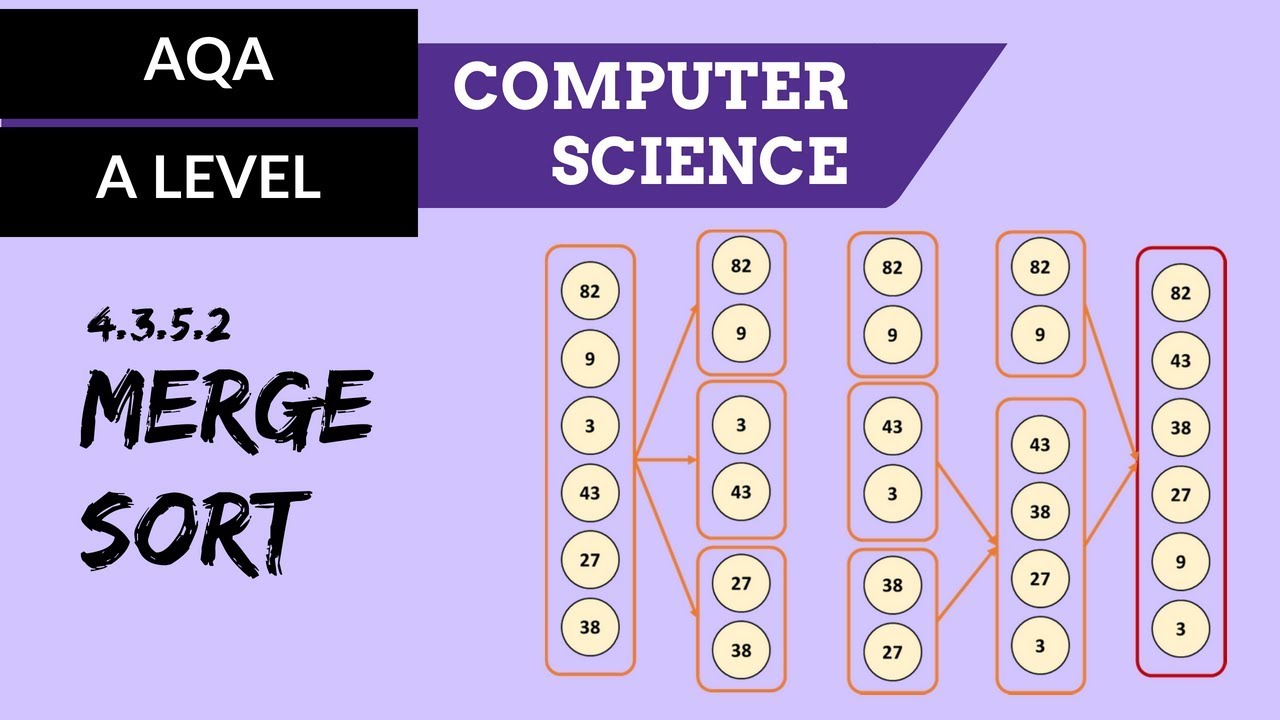
- 😀 MergeSort is a divide-and-conquer algorithm used for sorting arrays.
- 😀 The algorithm is recursive, meaning it repeatedly breaks down the problem into smaller subproblems.
- 😀 The core idea of MergeSort is to split an array into halves until each section contains only one element.
- 😀 Once the array is broken down, the elements are merged back together in sorted order.
- 😀 MergeSort’s efficiency comes from the fact that it sorts arrays by merging sorted subarrays.
- 😀 Time complexity of MergeSort is O(n log n), which makes it efficient even for large datasets.
- 😀 The 'n' in O(n) comes from the fact that every element needs to be visited during the merge process.
- 😀 The 'log n' comes from the depth of the recursive splitting, which creates a binary tree structure.
- 😀 In the merge step, two sorted arrays are compared and merged into a new sorted array.
- 😀 Although the recursive steps may seem reversed compared to implementation in code, thinking in terms of divide-and-conquer provides clarity.
Q & A
What is the main idea behind Merge Sort?
-Merge Sort is a divide-and-conquer algorithm where the problem (an unsorted array) is broken into smaller sub-problems, solved individually, and then the results are combined in sorted order.
How does Merge Sort divide the problem?
-Merge Sort recursively splits the array in half until each part contains only one element. Once broken down, the merging process begins.
What is the role of recursion in Merge Sort?
-Recursion in Merge Sort allows the array to be continually divided into smaller sub-arrays. The recursion ends when each sub-array contains just one item, at which point merging begins.
How does the merging process work in Merge Sort?
-In the merging process, two sorted sub-arrays are combined by comparing their elements and inserting them in the correct order to form a larger sorted array.
Why is Merge Sort considered a divide-and-conquer algorithm?
-Merge Sort is a divide-and-conquer algorithm because it breaks a large problem (sorting an unsorted array) into smaller sub-problems (sorting smaller arrays), which are solved individually and then combined.
What is the worst-case time complexity of Merge Sort?
-The worst-case time complexity of Merge Sort is O(n log n), where 'n' is the number of elements in the array. The O(n) part comes from the merging process, and the O(log n) comes from the depth of recursion.
How does the depth of recursion impact the time complexity of Merge Sort?
-The depth of recursion in Merge Sort is logarithmic (O(log n)) because the array is halved with each recursive step. This results in a logarithmic number of levels in the recursion tree.
Can Merge Sort be used for large datasets?
-Yes, Merge Sort is highly efficient for large datasets because its time complexity is O(n log n), making it faster than algorithms with higher time complexities like O(n^2), such as Bubble Sort.
What is the significance of the O(n) term in the time complexity of Merge Sort?
-The O(n) term in Merge Sort's time complexity comes from the fact that each element of the array must be visited during the merging process to ensure that the array is sorted.
What happens when the recursion reaches individual elements in Merge Sort?
-When recursion reaches individual elements, the merging process begins, where these single-element arrays are combined into larger sorted arrays by comparing and inserting elements in order.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)