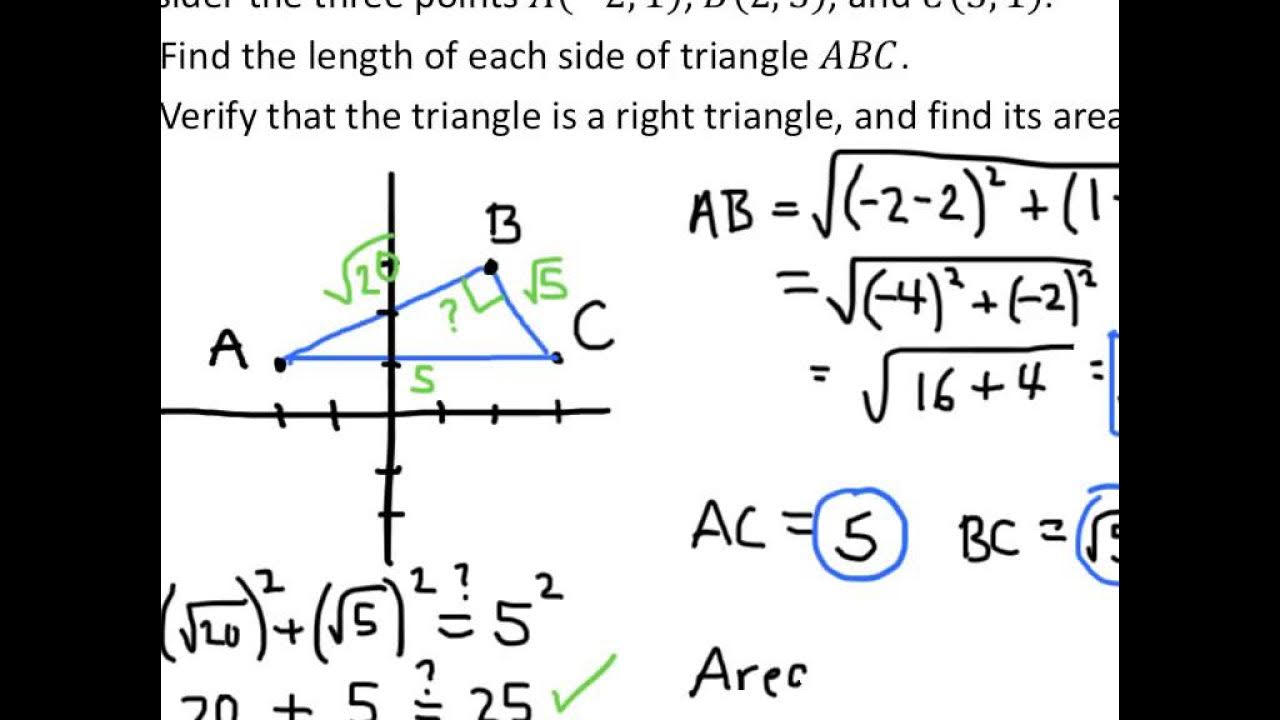
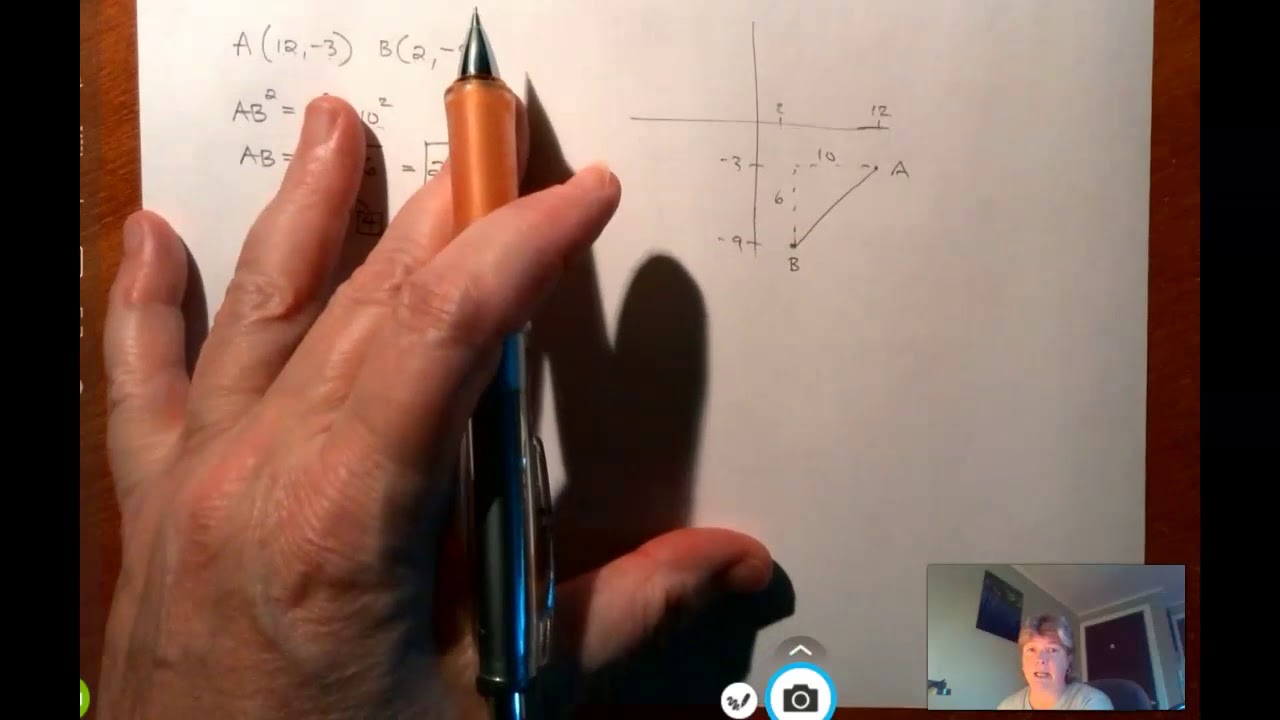
Class - 9th Ex - 8 Intro (Quadrilaterals) Maths New NCERT CBSE

Summary

This video provides a detailed explanation of essential triangle theorems, focusing on the midpoint theorem and its reverse. It demonstrates how the line joining midpoints of two sides of a triangle is parallel to and half the length of the third side. The reverse theorem shows how a line through the midpoint of one side, parallel to another side, bisects the third side. The concepts are crucial for understanding triangle properties and solving problems related to quadrilaterals. Viewers are encouraged to explore additional resources and engage with the content through likes, shares, and subscriptions.

Takeaways

• 😀 The mid-point theorem in triangles states that the line joining the midpoints of two sides is parallel to the third side and half its length.
• 😀 If two points, `E` and `F`, are midpoints of sides `AC` and `BC` respectively, then the line `EF` is parallel to side `AB` and half its length.
• 😀 The converse of the mid-point theorem tells us that if a line through the midpoint of one side is parallel to another side, it will bisect the third side.
• 😀 If `EF` is parallel to `AB`, then point `F` will bisect side `BC`, dividing it into two equal segments.
• 😀 The mid-point theorem applies to all triangles and helps in determining relationships between the sides and their midpoints.
• 😀 The line joining the midpoints of two sides in a triangle divides the third side into two equal parts if it is parallel to that side.
• 😀 The concept of parallel lines in triangles can be used to prove the equality of side segments, aiding in geometry problem-solving.
• 😀 The video encourages viewers to understand the mid-point theorem through both visual explanations and exercises for deeper learning.
• 😀 The theorem is a key concept in geometry and is likely to appear in exams, so it is important to thoroughly grasp its principles.
• 😀 The content also introduces quadrilaterals briefly, with references to other important concepts that complement triangle-based geometry.
• 😀 The video provides a call to action, encouraging viewers to like, share, and subscribe for more educational videos on related topics.

Q & A

What does the midpoint theorem state about a line segment joining the midpoints of two sides of a triangle?

The midpoint theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and is half of its length.

What happens when you join the midpoints of sides AB and BC of a triangle?

When the midpoints of sides AB and BC of a triangle are joined, the line formed is parallel to the third side (AC) and has half its length.

How does the second part of the midpoint theorem relate to the bisecting line?

The second part of the midpoint theorem states that if a line is drawn through the midpoint of one side of a triangle, it will be parallel to another side and will bisect the third side.

What is the significance of the points E and F in the explanation?

Points E and F are the midpoints of sides AB and BC, respectively. The line joining these points is parallel to side AC and half its length, demonstrating the midpoint theorem.

What conclusion can be drawn about the relationship between the line EF and side AC?

The line EF is parallel to side AC, and its length is half of AC, as per the midpoint theorem.

What does it mean for a line to bisect a side of a triangle?

To bisect a side of a triangle means to divide it into two equal parts. For example, the line joining the midpoints of two sides of a triangle will bisect the third side.

What happens if a line passes through the midpoint of one side of a triangle?

If a line passes through the midpoint of one side of a triangle, it will be parallel to another side of the triangle and will bisect the third side.

How does the midpoint theorem help solve problems related to triangles and quadrilaterals?

The midpoint theorem provides crucial properties for solving problems related to the geometry of triangles and quadrilaterals, especially when it comes to proving parallelism and proportionality of sides.

Why is it important to understand midpoint theorems for Class 9 mathematics?

Understanding midpoint theorems is essential in Class 9 mathematics as they are foundational concepts in geometry, often used to solve problems involving triangles, quadrilaterals, and other geometric shapes.

How can the midpoint theorem be applied in real-world geometry?

The midpoint theorem can be applied in various real-world scenarios, such as in architecture and design, where understanding the relationships between different parts of shapes and structures is necessary for creating balanced and proportional designs.