FISIKA KELAS XI - VENTURIMETER TANPA MANOMETER || FLUIDA DINAMIS
Summary
TLDRThis video tutorial explains the concept of a Venturi meter, focusing on how it measures fluid velocity without the use of a manometer. It breaks down the formula for calculating fluid speed at two different pipe cross-sections using the difference in fluid height. The video also demonstrates solving a real-world example, where the cross-sectional areas of a large and small pipe and the fluid height difference are given. The video concludes with a discussion of the continuity equation and its application to solve for fluid velocity, making the topic accessible to high school physics students.
Takeaways
- 😀 Venturimeter is a device used to measure the speed of a fluid based on pressure differences due to varying pipe diameters.
- 😀 The principle of operation involves the change in fluid velocity and pressure at two different sections of the Venturimeter.
- 😀 The equation for fluid velocity at section 1 (V1) is derived from the height difference (h) and cross-sectional areas (A1, A2).
- 😀 The velocity at section 1 can be calculated using the formula: V1 = sqrt(2gh * (A1/A2)^2).
- 😀 The velocity at section 2 can be found using the equation: V2 = sqrt(2gh * (A2/A1)^2).
- 😀 The gravitational acceleration (g) is typically assumed to be 10 m/s² when not specified in problems.
- 😀 The Continuity Equation (A1V1 = A2V2) is used to relate the velocities and areas at two sections of the Venturimeter.
- 😀 The flow speed at the larger cross-section (V1) and smaller cross-section (V2) are inversely related to their respective areas.
- 😀 A sample problem shows how to apply the formulas to find fluid velocities given the areas and height difference.
- 😀 The key to solving problems with a Venturimeter is correctly applying the relevant equations and continuity principle to calculate fluid velocities.
Q & A
What is a venturimeter and what is it used for?
-A venturimeter is a device used to measure the velocity of fluid flow. It operates by exploiting the difference in pressure that occurs when the fluid passes through sections of varying cross-sectional areas within a tube.
How does the difference in cross-sectional area affect fluid velocity in a venturimeter?
-The difference in cross-sectional areas between two sections of the venturimeter causes a change in fluid velocity. According to the principle of conservation of mass, the fluid speed increases in the narrower section and decreases in the wider section.
What happens to the pressure of the fluid when it passes through the narrower section of a venturimeter?
-As the fluid passes through the narrower section of the venturimeter, its velocity increases, which leads to a decrease in pressure, following the Bernoulli principle.
What formula is used to calculate the fluid velocity at the larger cross-sectional area (V1) in a venturimeter?
-The formula used to calculate the fluid velocity at the larger cross-sectional area is: V1 = √[2gH * (A1/A2)² - 1], where V1 is the velocity at point 1, g is the acceleration due to gravity, H is the height difference, A1 is the larger cross-sectional area, and A2 is the smaller cross-sectional area.
How do you calculate the velocity at the smaller cross-sectional area (V2) in a venturimeter?
-The velocity at the smaller cross-sectional area (V2) can be calculated using the formula: V2 = √[2gH * (A1/A2)² - 1], where the variables are defined similarly as in the calculation for V1. Alternatively, the continuity equation (A1 * V1 = A2 * V2) can also be used to solve for V2 after determining V1.
What is the role of the height difference (H) in the venturimeter velocity calculations?
-The height difference (H) between the two points of the venturimeter is directly proportional to the change in fluid velocity. A larger height difference leads to a greater difference in velocities between the two sections.
Why is gravity (g) important in the venturimeter equations, and what value should be used if it's not provided?
-Gravity (g) is a key factor in determining the fluid's potential energy, which affects its velocity. If the value of gravity is not provided, it is typically assumed to be 10 m/s² for simplicity in calculations.
In the example problem, what are the given values for the cross-sectional areas and height difference?
-In the example problem, the cross-sectional area at point 1 (A1) is 5 cm², the cross-sectional area at point 2 (A2) is 3 cm², and the height difference (H) is 0.2 meters.
How do you calculate the velocity at point 1 (V1) using the given data in the example problem?
-To calculate V1, we use the formula: V1 = √[2gH * (A1/A2)² - 1]. Substituting the known values (g = 10 m/s², H = 0.2 m, A1 = 5 cm², A2 = 3 cm²), the result for V1 is approximately 3.2 m/s.
How can the velocity at point 2 (V2) be calculated using the continuity equation?
-Using the continuity equation A1 * V1 = A2 * V2, we substitute the known values for A1, V1, and A2. After solving for V2, the result is 2.5 m/s, which is the velocity of the fluid at the smaller cross-sectional area.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Fluida Dinamis • Part 4: Venturimeter / Pipa Venturi
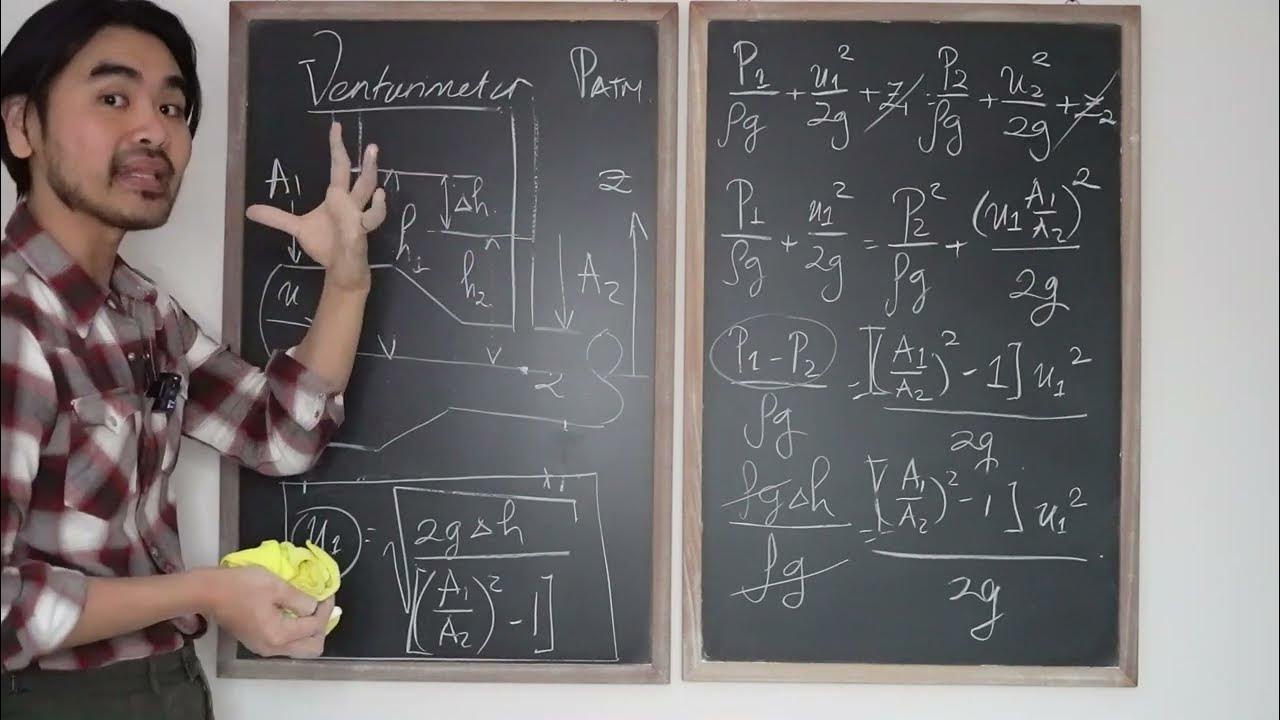
Mekanika Fluida FM01 (Lecture3: 6/8). Venturimeter - Aplikasi persamaan Bernoulli
FISIKA KELAS XI: PENERAPAN HUKUM BERNOULLI PADA PIPA VENTURIMETER

01 - Fluid Transport - Pitot Tube

Mekanika Fluida FM01 (Lecture3: 5/8). Kontinuitas (Continuity)

Mekanika Fluida FM01 (Lecture3: 7/8). Static-Pitot Tube
5.0 / 5 (0 votes)
