FISIKA KELAS XI: PENERAPAN HUKUM BERNOULLI PADA PIPA VENTURIMETER
Summary
TLDRThis video explains the application of Bernoulli's principle in a Venturi pipe. It describes how fluid velocity and pressure vary across different sections of the pipe, with the largest pressure observed in the section with the smallest flow velocity. The video further demonstrates the mathematical formulas used to calculate the flow velocity at various points in the pipe. Through practical examples, the presenter explains how to solve problems related to fluid velocity and pressure changes in a Venturi meter. Viewers are encouraged to interact by commenting with questions for clarification.
Takeaways
- 😀 Bernoulli's principle explains that in a horizontal pipe, the pressure of a fluid is highest where its speed is lowest and vice versa.
- 😀 A Venturi tube utilizes Bernoulli's principle to determine fluid flow speed based on the cross-sectional area of the tube.
- 😀 The speed of fluid increases when the cross-sectional area decreases, causing a drop in pressure at narrower sections of the pipe.
- 😀 To calculate the velocity of fluid entering and exiting the Venturi tube, specific formulas based on Bernoulli's principle are used.
- 😀 The velocity at section 1 (V1) is determined by the equation V1 = √(2 * G * Δh / (A1^2 - A2^2)).
- 😀 The velocity at section 2 (V2) is calculated using a similar formula with the appropriate cross-sectional areas and height difference.
- 😀 Example 1 shows how to calculate the fluid velocity at section 1 using the given cross-sectional areas and height difference.
- 😀 In Example 2, the velocity at both section 1 and section 2 is calculated for a new pipe scenario, with different cross-sectional areas and a height difference of 0.2 meters.
- 😀 The height difference (Δh) plays a key role in the fluid velocity calculation in a Venturi tube system.
- 😀 By applying the formulas and principles shown in the examples, you can easily determine the velocity of fluid at different points in a Venturi tube system.
Q & A
What is the main principle discussed in the video?
-The main principle discussed in the video is Bernoulli's Principle, which is applied to the Venturi pipe to explain how fluid flow and pressure behave at different points along the pipe.
How does Bernoulli's Principle relate to the Venturi pipe?
-In a Venturi pipe, Bernoulli's Principle explains that at a wider section of the pipe, the fluid velocity is lower, and the pressure is higher. In contrast, at a narrower section, the fluid velocity increases, and the pressure decreases.
What is the formula used to determine the velocity of fluid entering the Venturi pipe?
-The velocity of fluid entering the Venturi pipe (V1) can be calculated using the formula: V1 = sqrt(2 * g * h / (A1^2 - A2^2)) where g is the gravitational acceleration, h is the height difference, and A1 and A2 are the areas of the larger and smaller pipe sections, respectively.
How is the velocity of fluid exiting the Venturi pipe calculated?
-The velocity of fluid exiting the Venturi pipe (V2) can be determined using the formula: V2 = sqrt(2 * g * h / (A2^2 - A1^2)), where the variables represent the same parameters as in the formula for V1.
What do the variables A1 and A2 represent in the formulas?
-A1 represents the cross-sectional area of the larger section of the pipe, and A2 represents the cross-sectional area of the smaller section of the pipe. Both areas should be in square meters.
Why is the pressure higher at the larger section of the Venturi pipe?
-According to Bernoulli's Principle, when the fluid velocity is lower at the larger section of the pipe, the pressure increases. This is because energy conservation results in pressure increasing when the velocity decreases.
What happens to the fluid velocity and pressure at the smaller section of the Venturi pipe?
-At the smaller section of the Venturi pipe, the fluid velocity increases, and the pressure decreases. This is due to the conservation of energy, where a reduction in the cross-sectional area leads to an increase in velocity and a decrease in pressure.
What is the significance of the height difference (h) in the formula?
-The height difference (h) represents the difference in potential energy between two points in the pipe. It plays a key role in determining the velocity of the fluid at different points by impacting the overall energy balance of the system.
How do the units in the formulas need to be adjusted for proper calculation?
-In the formulas, the areas A1 and A2 should be in square meters (m²), the height difference (h) should be in meters (m), and gravitational acceleration (g) should be in meters per second squared (m/s²). Consistency in units is essential for accurate results.
Can you provide a brief explanation of how to solve a sample problem using these formulas?
-To solve a sample problem, first identify the known values such as the areas (A1, A2), the height difference (h), and gravitational acceleration (g). Then, use the formulas for V1 and V2 by plugging in the known values. For example, in one problem, the areas were given in cm², so they needed to be converted to m². After this, substitute the values into the formula and solve for the velocities.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
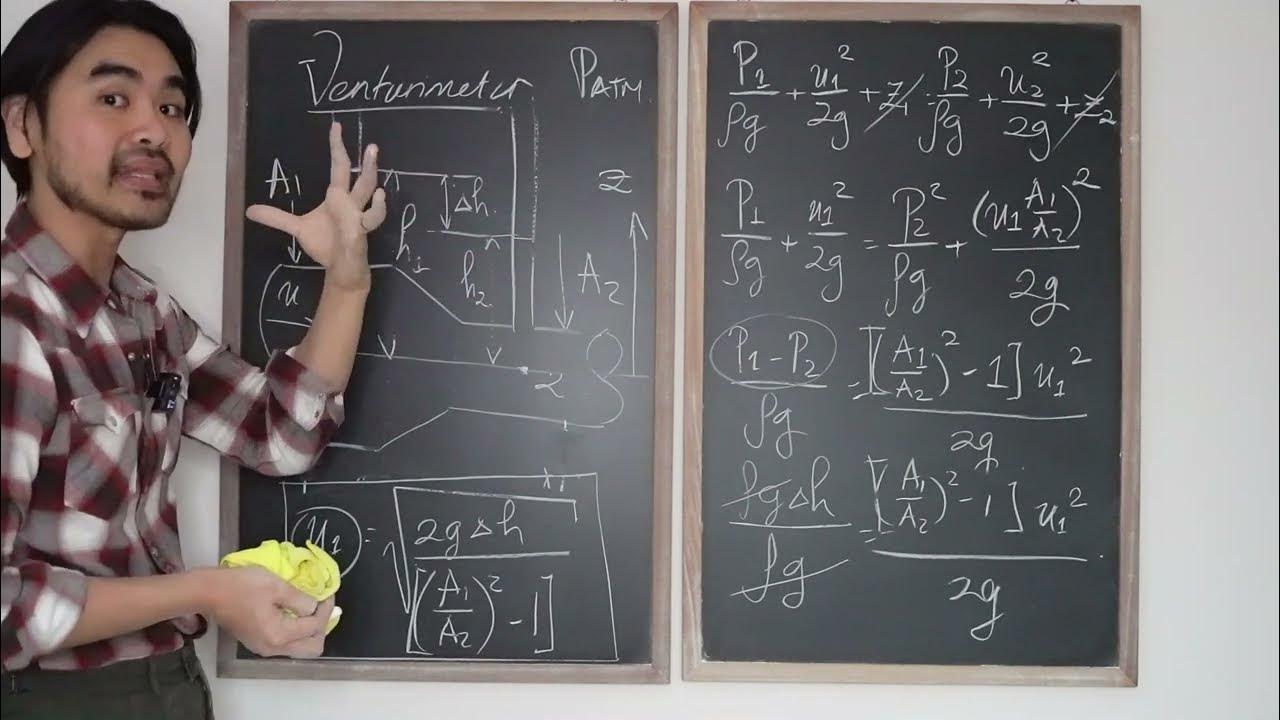
Mekanika Fluida FM01 (Lecture3: 6/8). Venturimeter - Aplikasi persamaan Bernoulli

Fluida Dinamis - Konsep Bernoulli - Simple Konsep - Fisika Kelas 11

Mekanika Fluida FM01 (Lecture3: 7/8). Static-Pitot Tube

Bernoulli's Principle Derivation

Fluid Dynamics VII: The Venturi Effect

FISIKA KELAS XI - VENTURIMETER TANPA MANOMETER || FLUIDA DINAMIS
5.0 / 5 (0 votes)