Convert Rectangular to Polar Coordinates, SOLVED EXAMPLES, All QUADRANTS
Summary
TLDR本视频介绍了如何在极坐标系统中计算角度和半径。通过示范如何处理负角度和不精确的结果,讲解了两种常见的方法:一种是通过从正角度减去360度获得负角度,另一种是直接从图形中得出。视频还展示了如何计算半径和角度,使用了反正切公式和根号计算。无论是求解精确结果还是使用小数值,都详细解释了计算步骤,帮助观众更好地理解极坐标系统中的转换与计算。
Takeaways
- 😀 通过将正角度减去360°,可以转换成负角度 (如210°减去360°等于-150°)。
- 😀 通过从图形上直接测量,可以更直观地计算负角度,特别是通过减去30°得到-150°。
- 😀 负角度在计算时可以使用正数的坐标进行公式运算,最终得出角度值。
- 😀 用反正切函数(tan⁻¹)来计算角度,得到辅助角度α(如tan⁻¹(3))。
- 😀 在计算时,可以将角度结果以精确值(如tan⁻¹(3))或十进制形式(如71.57°或1.25弧度)表达。
- 😀 极坐标的计算需要两个值:r(径向距离)和θ(角度)。
- 😀 通过减去辅助角α,可以得出极坐标角度θ,得出结果如180°-α或π-α。
- 😀 当角度是负数时,可以转换为相应的正角度形式,进行更方便的计算。
- 😀 极坐标可以精确地表示为根号形式(如√10)或使用计算器进行近似值计算(如1.89弧度)。
- 😀 在讲解结束时,感谢支持YouTube会员的人,表示感谢并鼓励继续支持。
- 😀 计算结果既可以表示为小数形式,也可以用符号表示,依据需要选择合适的形式。
Q & A
如何计算负角度?
-有两种方法可以计算负角度:第一种方法是从一个正角度中减去360度;第二种方法是通过绘图,从参考点(例如180度)中减去已知的角度来得到负角度。
如何将角度转换为弧度?
-可以将角度乘以π/180来转换为弧度。比如-150度转换为弧度是-5.24弧度。
如何计算极坐标中的r值?
-极坐标中的r值是通过计算点到原点的距离来得到的,可以使用公式r = √(x² + y²)。例如,给定坐标(-1, 3),r = √(1 + 9) = √10。
如何计算辅助角alpha?
-辅助角alpha是指从x轴开始的角度,可以通过反正切函数来计算,公式为tan(alpha) = y / |x|,其中y和x分别是坐标的y值和x值的绝对值。
如何得到极坐标中的θ角度?
-θ角度可以通过从180度减去辅助角alpha来计算,尤其是在第二象限时。这样,θ = 180° - alpha,或者在弧度制下,θ = π - alpha。
如何表达极坐标中的角度结果?
-极坐标中的角度结果可以用两种方式表示:一种是精确表示,使用反正切函数,如π - tan⁻¹(3);另一种是以小数形式表示,如108.43度或1.89弧度。
如何处理不精确的数值结果?
-对于不精确的结果,可以选择保留精确的形式,例如使用反正切函数的形式,也可以使用小数形式来近似表达结果。
在第二象限中,如何判断极坐标的角度?
-在第二象限中,极坐标的角度θ通常是180度减去计算得到的辅助角alpha,这样能够确保角度朝向第二象限。
如何在计算中使用反正切函数?
-反正切函数用于计算一个角度,公式为alpha = tan⁻¹(y / x),其中x和y是给定点的坐标。在实际计算中,可以用计算器得到角度的近似值。
如何在实际应用中使用极坐标?
-极坐标通常用于描述二维空间中的点,尤其在涉及旋转或对称性时。通过计算r和θ,可以方便地将直角坐标系中的点转换为极坐标系,便于解决问题或进行图形分析。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
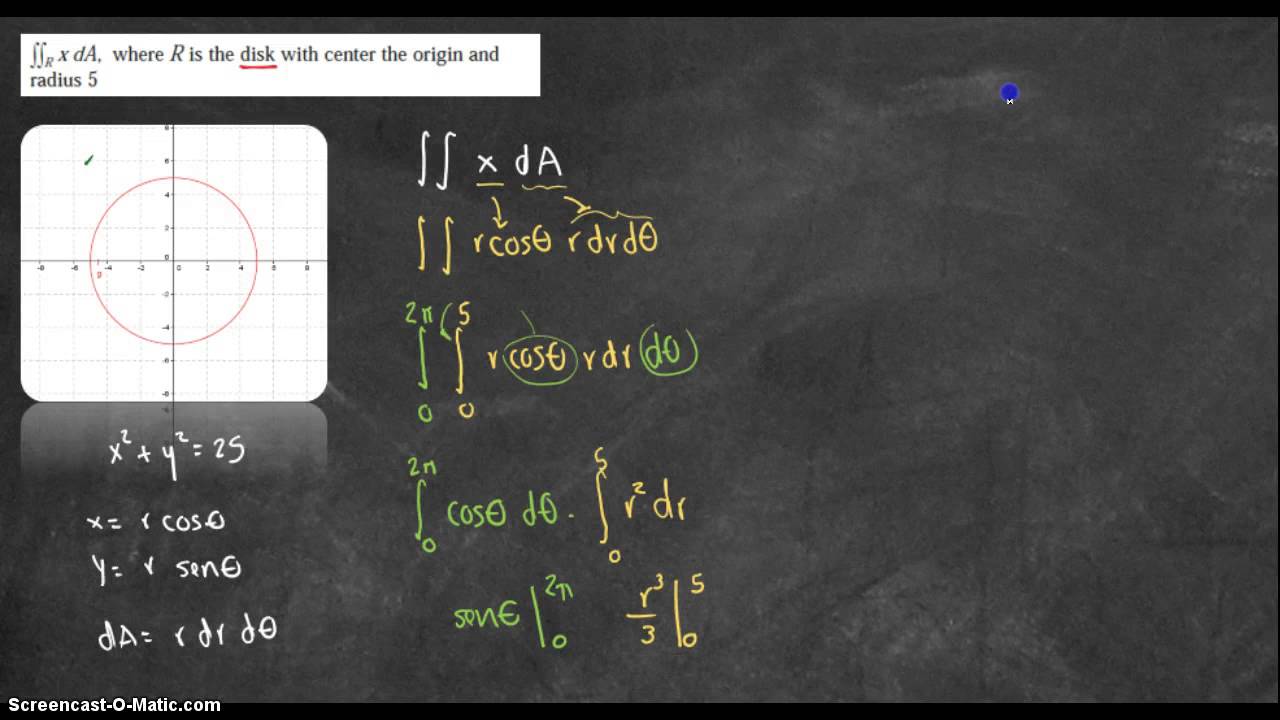
Ejemplo 01 - Ingtegrales polares
Introduction to windows | computer software language learning | Computer Education for All

Computer Vision: Crash Course Computer Science #35

Psychology of Computing: Crash Course Computer Science #38

Autopista - Fuerzas de resistencia en tu vehículo

Aceleraciones en un Movimiento Circular.
5.0 / 5 (0 votes)