LENGKAP Integral tak tentu, integral tertentu, integral subtitusi dan integral parsial
Summary
TLDRThis educational video from 'Matematika Hebat' offers a comprehensive guide to understanding various types of integrals, including indefinite integrals, definite integrals, substitution integrals, and integration by parts. It begins with foundational concepts, introducing the basic formulas for indefinite integrals, followed by step-by-step solutions to example problems. The video also covers how to solve definite integrals with limits, and how substitution and integration by parts methods are applied. The tutorial aims to simplify complex mathematical concepts for students, providing clear explanations and practical problem-solving techniques.
Takeaways
- 😀 Understanding the basic formula for indefinite integrals is crucial to solving related problems efficiently.
- 😀 The general formula for indefinite integrals includes adding 1 to the exponent and dividing by the new exponent.
- 😀 When solving indefinite integrals, always remember to add the constant 'C' at the end of the expression.
- 😀 For definite integrals, the formula remains the same as for indefinite integrals, but you apply the upper and lower bounds at the end.
- 😀 The process for solving definite integrals involves evaluating the integral at the upper and lower bounds, then subtracting the two results.
- 😀 Substitution integrals are useful when the derivative of a function inside the integral matches the function outside the integral.
- 😀 A substitution integral can be simplified by setting a part of the integrand as 'U', then replacing the differential in terms of 'du'.
- 😀 To perform integration by substitution, replace the expression inside the integral with a simpler variable (U), then adjust the differential accordingly.
- 😀 Integration by parts involves breaking down a product of functions into simpler parts using the formula: ∫udv = uv - ∫vdu.
- 😀 For integrals with roots, such as square roots, rewrite the expression in exponent form before applying the appropriate integration method.
Q & A
What is the basic formula for an indefinite integral of the form ∫ax^n dx?
-The basic formula for an indefinite integral of the form ∫ax^n dx is: (a / (n+1)) * x^(n+1) + C, where 'a' is a constant and 'n' is the exponent of x.
How do you solve the indefinite integral ∫(2x^3 - 6x^2 + 8x + 2) dx?
-To solve this integral, apply the basic power rule to each term: For 2x^3, use (2/4)x^4, for -6x^2, use (-6/3)x^3, for 8x, use (8/2)x^2, and for 2, use 2x. Then simplify the result and combine like terms.
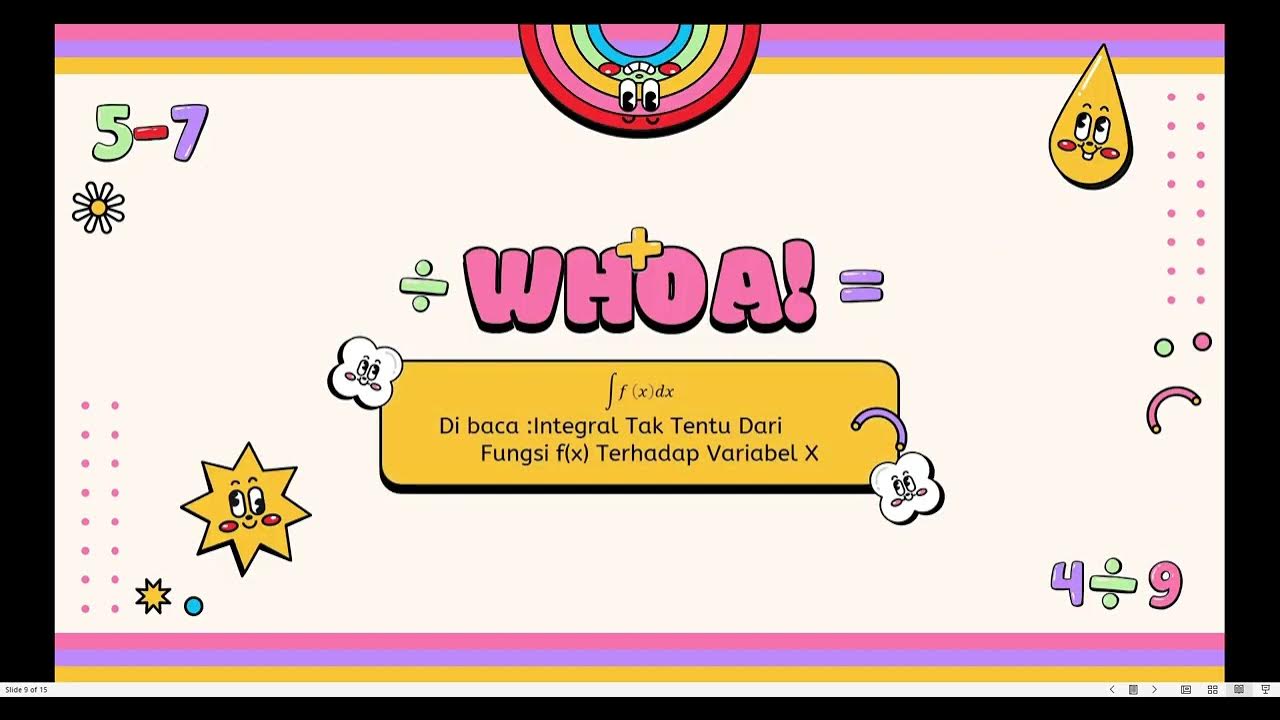
What is the main difference between an indefinite integral and a definite integral?
-The main difference is that a definite integral has upper and lower limits, which must be applied to the result after integration, while an indefinite integral does not have limits and includes a constant 'C' to represent the general solution.
How do you solve a definite integral like ∫(3x² - 15x - 18) dx with limits from 0 to 2?
-For a definite integral, first integrate each term using the power rule. Then substitute the upper limit (2) and lower limit (0) into the integrated expression and subtract the value at the lower limit from the value at the upper limit.
In the substitution method, how do you determine when to use it for solving an integral?
-Use substitution when part of the integrand can be simplified by setting a new variable (u) equal to an expression within the integral, and its derivative appears elsewhere in the integral, making the integral easier to solve.
What is the substitution method for the integral ∫4x(4x² - x - 3)^4 dx?
-For the substitution method, let u = 4x² - x - 3, then find du/dx, which is 8x - 1. Substitute the values of u and du into the integral to simplify it, then solve the resulting integral in terms of u, and finally substitute back the expression for u.
What makes a substitution integral different from integration by parts?
-A substitution integral is typically used when there is a clear part of the integrand whose derivative is present elsewhere in the integral, while integration by parts is used when the integrand is a product of two functions that can be separated into parts.
How do you perform integration by parts on the integral ∫(x + 3)√(2x - 5) dx?
-First, rewrite √(2x - 5) as (2x - 5)^(1/2). Then, use the integration by parts formula: ∫u dv = uv - ∫v du. Choose u = (x + 3) and dv = (2x - 5)^(1/2). Compute du and v, and apply the integration formula to solve the integral.
What is the key formula used in integration by parts?
-The key formula for integration by parts is ∫u dv = uv - ∫v du, where 'u' and 'dv' are parts of the integrand that are chosen to simplify the integral.
Why is it important to simplify the integrand before applying integration techniques?
-Simplifying the integrand before applying integration techniques helps to reduce complexity, making the integral easier to solve and ensuring that the chosen method, such as substitution or integration by parts, is applicable.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

MATEMATIKA Kelas 11 - Integral Tak Tentu | GIA Academy

Konsep Dasar Integral Fungsi Aljabar (Integral Part 1) M4THLAB
Menemukan Konsep Integral tak Tentu sebagai kebalikan dari Turunan

Integral (Tak Tentu)

INTEGRAL LIPAT 2 #KALKULUS 2

Integration | Finite | Infinite | شرح قواعد التكامل المحدود وغير المحدود Part (1)FCES
5.0 / 5 (0 votes)
