Integration | Finite | Infinite | شرح قواعد التكامل المحدود وغير المحدود Part (1)FCES

Summary

The video lecture provides a detailed explanation of integration in mathematics, focusing on both definite (limited) and indefinite (unlimited) integrals. It outlines key principles and rules of integration, such as handling constants, the general form of integrals, and the importance of including a constant of integration in indefinite integrals. The speaker explains techniques like integrating powers of x, constants, and special cases like 1/x. It also covers the process of solving definite integrals, including step-by-step evaluation. The session concludes with a reminder of the core concepts and a call for reflection on the material learned.

Takeaways

• 😀 Integration is the reverse process of differentiation, used to find areas under curves or accumulate values.
• 😀 Definite integrals have a clear start and end, marked by lower and upper bounds, while indefinite integrals are without such bounds.
• 😀 In definite integrals, the result is the difference between the upper limit and the lower limit after applying the integration rule.
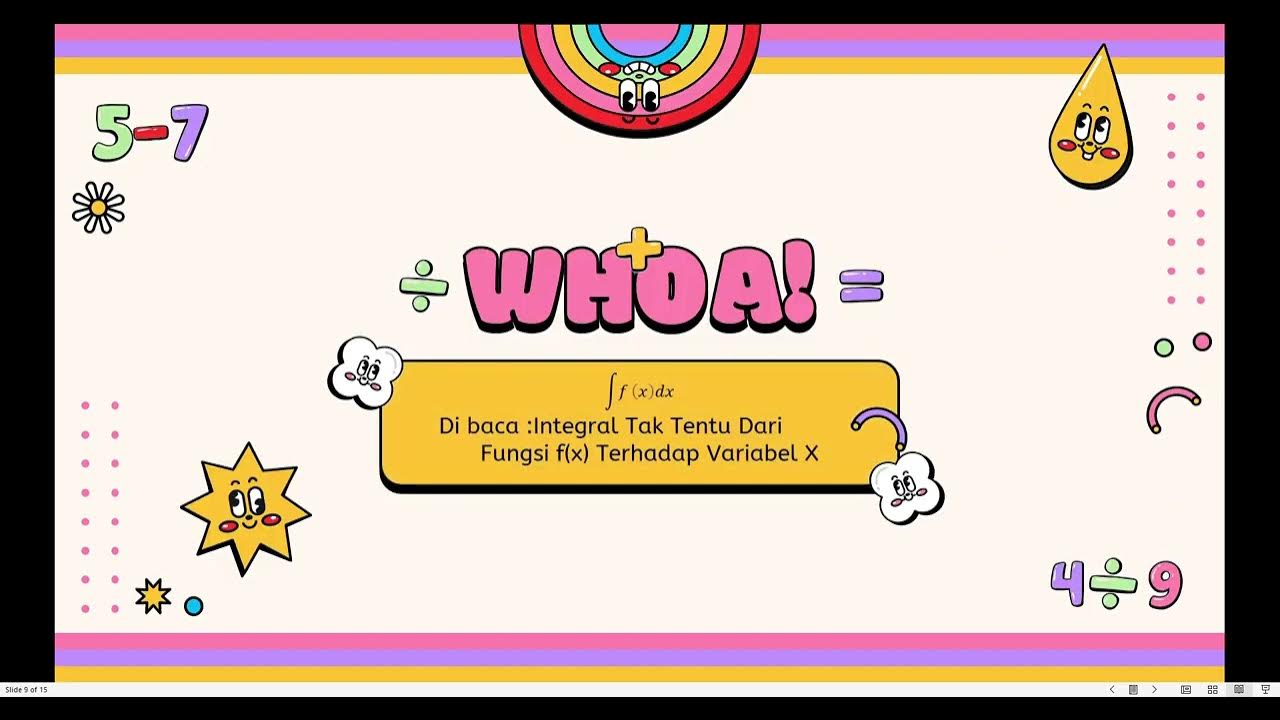
• 😀 In indefinite integrals, a constant of integration (denoted as 'C') is added, representing an unknown constant value.
• 😀 It's important to follow the notation correctly: 'dx' represents the variable with respect to which you're integrating.
• 😀 For basic powers of 'x', the integration rule is to increase the exponent by one and divide by the new exponent.
• 😀 A constant factor can be pulled out of the integral, simplifying the expression.
• 😀 The integration of simple constants (e.g., 10 or 300) results in multiplying the constant by 'x', followed by the constant of integration.
• 😀 The integration of 1/x results in the natural logarithm of the absolute value of x.
• 😀 Special cases like the integral of e^x follow specific rules where the result is the exponential function itself, along with a constant.
• 😀 In definite integrals, the result is calculated by substituting the limits into the integrated function and subtracting the value at the lower limit from the value at the upper limit.

Q & A

What is the main topic of the video?

The main topic of the video is integration, specifically focusing on both definite and indefinite integrals, and the rules involved in solving integration problems.

What is the difference between definite and indefinite integration?

Definite integration has both upper and lower limits, represented by specific numbers, while indefinite integration does not have any limits and includes an arbitrary constant, typically denoted as 'C'.

How is the constant of integration represented in indefinite integrals?

In indefinite integrals, the constant of integration is usually represented as 'C' or 'c', depending on the convention of the institution or the lecturer.

How do you handle a constant term during integration?

When integrating a constant term, the rule is to multiply the constant by 'x' and then add the constant of integration (C). For example, the integral of 10 with respect to x is 10x + C.

What is the rule for integrating a power of x?

The rule for integrating a power of x is to increase the exponent by one and then divide by the new exponent. For example, the integral of x^n is (x^(n+1))/(n+1) + C.

What is the formula for integrating a function of the form 1/x?

The integral of 1/x with respect to x is the natural logarithm of the absolute value of x, i.e., ln|x| + C.

How do you integrate an expression with a coefficient like 300 or 15?

When integrating an expression like 300 or 15, the coefficient is multiplied by 'x' and then the constant of integration 'C' is added. For instance, the integral of 300 with respect to x is 300x + C.

What is the special case of integrating an exponential function?

The integral of an exponential function, such as e^x, is itself, i.e., e^x + C. If the exponent is more complicated, such as e^(5x), the integral is e^(5x)/5 + C.

What is the method for performing definite integration?

In definite integration, you substitute the upper limit and subtract the result from the lower limit. For example, for an integral from a to b, the result is F(b) - F(a), where F(x) is the antiderivative.

What happens if you do not add the constant of integration in definite integrals?

In definite integrals, the constant of integration is not included because the result depends only on the difference between the values of the antiderivative at the upper and lower limits. Thus, the constant cancels out.