Konsep Dasar Turunan Fungsi Aljabar Matematika Wajib Kelas 11 m4thlab
Summary
TLDRIn this educational video, Deni Handayani explains the concept of derivatives in algebraic functions, beginning with the definition and gradually moving into derivative rules. He demonstrates how to calculate the derivative using the limit definition, followed by simplifying the process with various derivative rules, such as the power rule, product rule, quotient rule, and chain rule. Through examples and step-by-step explanations, viewers learn how to differentiate algebraic functions effectively, with a focus on clarity and simplicity. The video is aimed at helping students understand the core principles of differentiation in calculus.
Takeaways
- 😀 The video covers the concept of derivatives and algebraic functions, starting with definitions and basic differentiation rules.
- 😀 The derivative of a function represents the slope of the tangent line at any given point, calculated using limits.
- 😀 The definition of a derivative involves calculating the limit of the difference in function values over a small interval as that interval approaches zero.
- 😀 In practice, using the limit-based definition of a derivative can be tedious, so more efficient methods are introduced.
- 😀 The power rule is a quick method for differentiating algebraic functions, where the derivative of ax^n is n * ax^(n-1).
- 😀 An example is provided to differentiate the function f(x) = 8x + 7 using the power rule.
- 😀 The video demonstrates how to compute the derivative of more complex polynomial functions like f(x) = 6x^3 - 13x^2 + 4x + 7.
- 😀 Derivatives of more complicated functions, including rational and root functions, are calculated by first simplifying them into easier forms.
- 😀 The product rule for derivatives is introduced, showing how to differentiate a product of two functions: y = u * v.
- 😀 The quotient rule for derivatives is explained, where the derivative of a quotient y = u/v is calculated using the formula y' = (v * u' - u * v') / v^2.
- 😀 The chain rule is introduced for differentiating composite functions, explaining how to differentiate an outer function and then multiply by the derivative of the inner function.
Q & A
What is the definition of a derivative in algebraic functions?
-The derivative of an algebraic function is the rate of change of the function with respect to its independent variable. It is represented by the limit of the difference quotient as the distance between two points approaches zero. This is expressed as the limit of (f(x+h) - f(x)) / h as h approaches zero.
How do you compute the derivative of the function f(x) = 8x + 7 using the definition?
-To compute the derivative using the definition, you calculate the difference quotient: (f(x+h) - f(x)) / h. For f(x) = 8x + 7, substituting into the formula and simplifying gives the result as 8, which is the derivative.
Why is using the definition of the derivative not always practical for algebraic functions?
-Using the definition of the derivative involves calculating limits and simplifying expressions for each term, which can be time-consuming and complex. This method is often not efficient for functions with many terms or complex expressions.
What is the power rule for finding the derivative of a function?
-The power rule states that for a function f(x) = ax^n, where a is a constant and n is a real number, the derivative is f'(x) = n * ax^(n-1). You multiply the exponent by the coefficient and subtract 1 from the exponent.
How do you apply the power rule to find the derivative of f(x) = 6x^3 - 3x^2 + 4x + 7?
-Using the power rule for each term: the derivative of 6x^3 is 18x^2, the derivative of -3x^2 is -6x, the derivative of 4x is 4, and the derivative of the constant 7 is 0. Thus, the derivative is f'(x) = 18x^2 - 6x + 4.
What is the derivative of a rational function, and how do you compute it?
-The derivative of a rational function, f(x) = u(x) / v(x), is found using the quotient rule. The quotient rule states that f'(x) = (v(x) * u'(x) - u(x) * v'(x)) / [v(x)]^2. You differentiate the numerator and denominator separately, then apply the formula.
How do you differentiate f(x) = 2x^2 - 4 / (4x + 1)?
-First, apply the quotient rule. The numerator u(x) = 2x^2 - 4 and the denominator v(x) = 4x + 1. The derivatives are u'(x) = 4x and v'(x) = 4. Substituting these into the quotient rule formula gives the final derivative.
What is the chain rule and how is it applied in differentiation?
-The chain rule is used to differentiate composite functions. If y = f(g(x)), the derivative is dy/dx = f'(g(x)) * g'(x). This means you differentiate the outer function and multiply it by the derivative of the inner function.
How would you use the chain rule to differentiate f(x) = (2x^2 - 2)^2021?
-First, differentiate the outer function, which is (2x^2 - 2)^2021. The derivative of this is 2021 * (2x^2 - 2)^2020 * 4x (the derivative of 2x^2 - 2). The final derivative is 8084x * (2x^2 - 2)^2020.
What is the derivative of f(x) = 2x^2 + 3x - 1 raised to the power of 3, evaluated at x = 2?
-To differentiate f(x) = (2x^2 + 3x - 1)^3, first apply the chain rule. The derivative is 3 * (2x^2 + 3x - 1)^2 * (4x + 3). Substituting x = 2 into this gives f'(2) = 3 * (2(2)^2 + 3(2) - 1)^2 * (4(2) + 3). This simplifies to f'(2) = -15.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Komposisi Fungsi Part 1 - Operasi Aljabar Pada Fungsi [ Matematika Wajib Kelas X ]
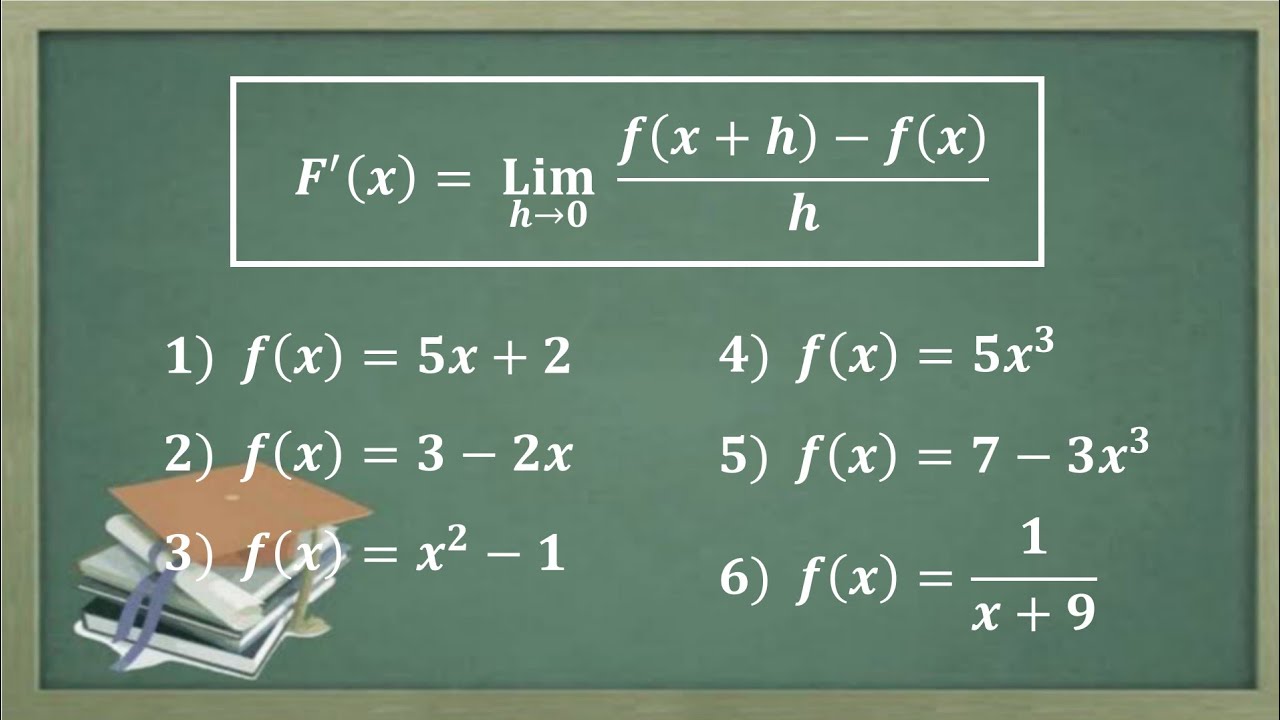
Turunan dengan menggunakan defnisi turunan Turunan menggunakan limit

Derivadas de funciones algebraicas (parte 1)

Aturan Turunan | Turunan (Part 2) | Kalkulus

Konsep Dasar dan Sifat-sifat Logaritma Matematika Peminatan Kelas 10
Fungsi Transenden 1 (Logaritma Natural/Ln)
5.0 / 5 (0 votes)
