Derivada de un cociente | Reglas de derivación
Summary
TLDREn este video, se explica cómo encontrar la derivada de una función que es un cociente, utilizando la regla del cociente. Se aborda el proceso paso a paso, identificando las funciones en el numerador y denominador, luego aplicando la fórmula de la derivada del cociente. El instructor resalta la importancia de practicar, mostrando cómo derivar funciones simples y cómo simplificar la expresión resultante. Al final, se presenta un ejercicio práctico para que los estudiantes refuercen lo aprendido. La clase está dirigida a quienes deseen comprender y practicar derivadas de cocientes en cálculo.
Takeaways
- 😀 La derivada de un cociente se puede calcular mediante la fórmula: (h(x) * g'(x) - g(x) * h'(x)) / (h(x))^2.
- 😀 Para calcular la derivada, primero se deben obtener las derivadas de las funciones involucradas, tanto la del numerador como la del denominador.
- 😀 La derivada de una constante, como 3, es igual a cero.
- 😀 La derivada de una función como 2x es simplemente 2.
- 😀 El proceso de derivación de un cociente incluye multiplicar el denominador por la derivada del numerador y restar el numerador por la derivada del denominador.
- 😀 Es importante recordar que al multiplicar términos con variables, se deben sumar los exponentes de las mismas.
- 😀 Se deben realizar operaciones y simplificaciones tras aplicar la fórmula para obtener la derivada en su forma más sencilla.
- 😀 El signo negativo en la fórmula debe aplicarse correctamente a todos los términos posteriores, ya que afecta a toda la expresión.
- 😀 En caso de que haya términos semejantes, se deben combinar (sumar o restar) para simplificar la expresión final de la derivada.
- 😀 Es fundamental aprender a factorizar expresiones algebraicas para simplificar la derivada y eliminar términos comunes, lo cual facilita su cálculo.
Q & A
¿Cómo se encuentra la derivada de una función cociente?
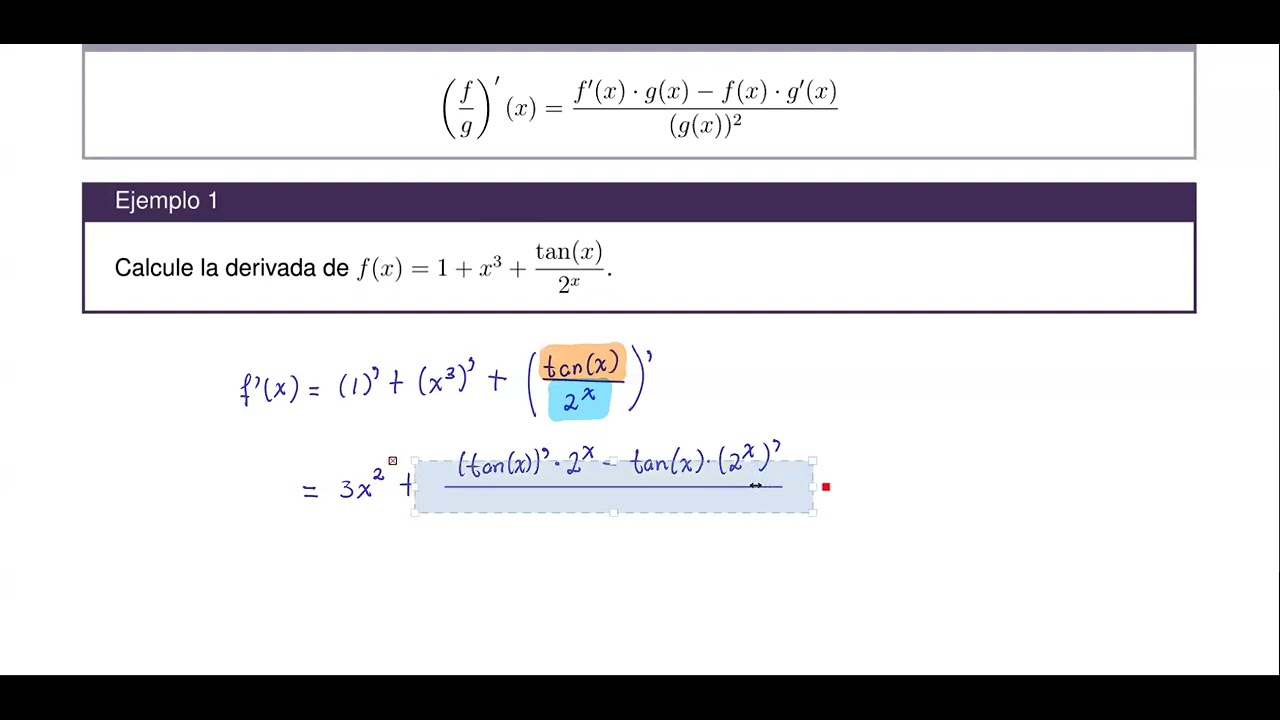
-Para encontrar la derivada de una función cociente, se usa la fórmula: (h(x) * g'(x) - g(x) * h'(x)) / (h(x))^2, donde g(x) es la función del numerador y h(x) la del denominador.
¿Qué significa que la derivada de una constante sea cero?
-Cuando derivamos una constante, el resultado es cero, ya que las constantes no cambian y su tasa de cambio es nula.
¿Cómo se derivan expresiones con exponente negativo?
-Para derivar una expresión con exponente negativo, aplicamos la regla de la potencia, bajando el exponente y restando uno. Por ejemplo, la derivada de x^(-n) es -n * x^(-n-1).
¿Qué se debe hacer antes de aplicar la regla del cociente?
-Antes de aplicar la regla del cociente, es fundamental calcular las derivadas de las funciones que están en el numerador y en el denominador.
¿Qué se entiende por términos semejantes al derivar?
-Los términos semejantes son aquellos que tienen las mismas potencias de la variable. Al derivar, si aparecen términos semejantes, se deben combinar sumando o restando sus coeficientes.
¿Cuál es el propósito de factorizar en el proceso de derivación?
-El propósito de factorizar es simplificar la expresión, eliminando factores comunes y facilitando el cálculo, lo que ayuda a obtener una forma más sencilla de la derivada.
¿Por qué se recomienda practicar ejercicios adicionales al aprender derivadas de cocientes?
-Practicar ejercicios adicionales ayuda a afianzar el conocimiento, entender mejor los conceptos y familiarizarse con las diferentes variaciones de las derivadas de cocientes.
¿Qué sucede cuando se tiene una resta en el numerador de una fracción al derivar?
-Cuando hay una resta en el numerador, no se puede simplificar como si fuera una multiplicación, ya que la resta no permite eliminar factores. Debe tratarse término por término.
¿Cómo se simplifica una expresión después de derivar un cociente?
-Una vez que se deriva el cociente, se deben combinar los términos semejantes y, si es posible, factorizar para simplificar la expresión, eliminando términos comunes.
¿Cuál es la importancia de la regla del cociente en el cálculo de derivadas?
-La regla del cociente es esencial para derivar funciones que son divisiones de dos funciones, ya que proporciona una manera estructurada de abordar y simplificar el proceso.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Derivada de un cociente | Ejemplo 2 | Reglas de derivación
Derivadas (Regla del cociente) 1

Derivadas de orden superior - Ej. 2

Derivadas (Regla del cociente 2)

Ejercicio a2.01 - Derivadas (la tangente a una parábola)

Máximo relativo, mínimo relativo, intervalos de crecimiento y decrecimiento de una función
5.0 / 5 (0 votes)
