Electrical Engineering: Ch 8: RC & RL Circuits (11 of 43) The L/R Time Constant

Summary

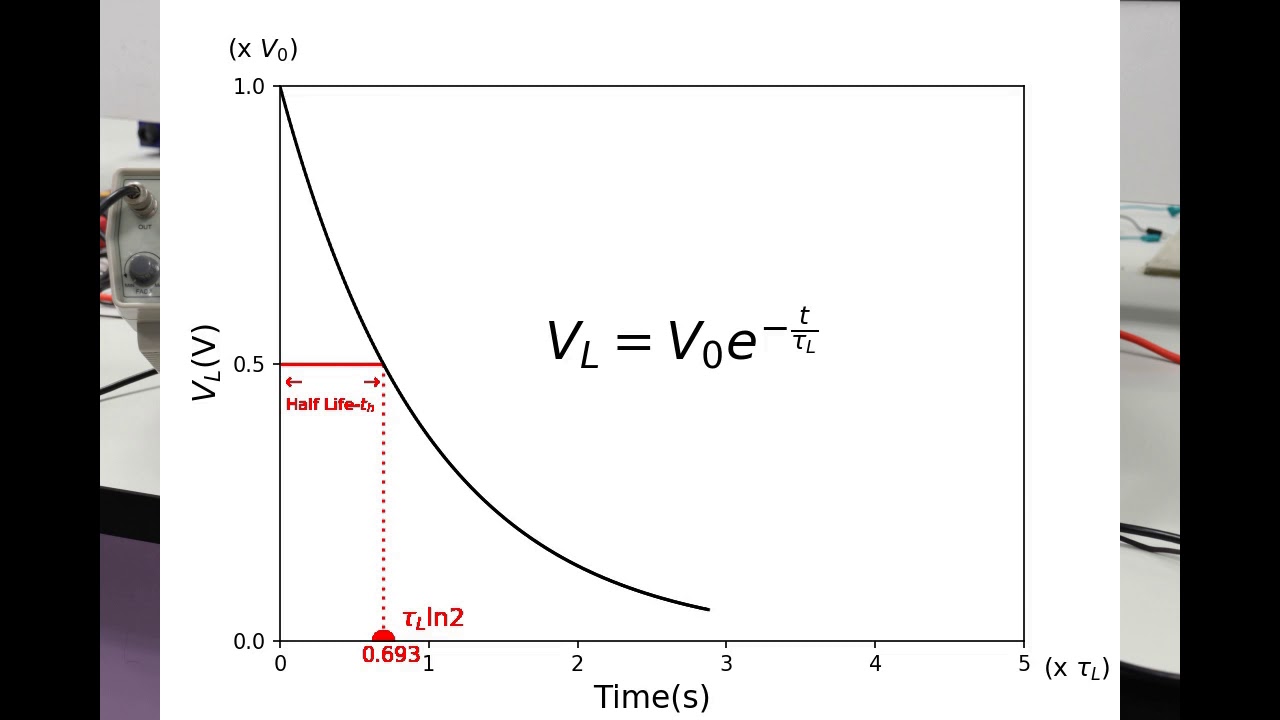
This video explains the behavior of current in an RL (resistor-inductor) circuit, emphasizing its exponential decay, similar to voltage in an RC (resistor-capacitor) circuit. The time constant, defined as L/R (inductance divided by resistance), dictates how quickly the current decreases. A larger inductance prolongs the decay, while greater resistance accelerates it. After specific time constants, the current significantly drops, reaching near-zero after five time constants. An example calculation illustrates this concept with an inductor of 0.2 Henrys and 20 ohms of resistance, showcasing the practical implications of these electrical principles.

Takeaways

• 😀 The current in an RL circuit decreases exponentially, similar to voltage in an RC circuit.
• 😀 The time constant in an RL circuit is calculated as tau = L / R, where L is inductance and R is resistance.
• 😀 Larger inductance results in a slower decline of current, as it opposes changes in current flow.
• 😀 Increased resistance leads to a faster drop in current, as per Ohm's Law (I = V / R).
• 😀 After one time constant, the current falls to approximately 36.8% of its initial value.
• 😀 After two time constants, the current drops to about 13.5% of its initial value.
• 😀 The current decreases to around 5% after three time constants and about 1.8% after four time constants.
• 😀 After five time constants, the current in the circuit is considered virtually zero, less than 1%.
• 😀 An example with 0.2 Henrys of inductance and 20 Ohms of resistance results in a time constant of 0.01 seconds.
• 😀 This understanding of RL circuits is crucial for analyzing transient responses in electrical systems.

Q & A

What is the main focus of the video regarding RL circuits?

The video focuses on the exponential decay of current in RL circuits, similar to voltage decay in RC circuits, and discusses the concept of time constants.

How is the time constant defined in an RL circuit?

The time constant in an RL circuit is defined as the inductance (L) divided by the resistance (R).

What role does an inductor play in an RL circuit?

An inductor opposes changes in current, which slows down the decay of current in the circuit as energy is dissipated through the resistor.

How does resistance affect the time constant in an RL circuit?

A larger resistance results in a smaller time constant, leading to a faster decrease in current. Conversely, a smaller resistance results in a larger time constant and a slower decrease.

What is the mathematical expression for current decay in an RL circuit?

The current can be expressed as I = I₀ * e^(-T/τ), where I₀ is the initial current, T is time, and τ is the time constant.

What does the exponential decay of current indicate after multiple time constants?

After five time constants, the current is typically considered to be virtually zero, meaning it has diminished to a negligible level.

Can you provide an example calculation for time constant in an RL circuit?

If the inductance is 0.2 Henrys and the resistance is 20 ohms, the time constant would be τ = L/R = 0.2 H / 20 Ω = 0.01 seconds.

What happens to the current as the time progresses in an RL circuit?

As time progresses, the current in the circuit decreases exponentially due to the combined effects of resistance and inductance.

Why does a larger inductor result in a longer time constant?

A larger inductor increases the time constant because it opposes changes in current more effectively, leading to a slower rate of current decay.

How does Ohm's Law relate to the behavior of current in RL circuits?

Ohm's Law states that current is equal to voltage divided by resistance. Therefore, as resistance increases, the overall current in the circuit decreases, affecting the time it takes for current to diminish.