Electrical Engineering: Ch 8: RC & RL Circuits (13 of 43) Current=? in RL Circuit: Ex. 1

Summary

This video explains how to analyze the current through an inductor in an RL circuit. It begins with a 10 V source connected to resistors and an inductor, detailing the steady-state condition before a switch opens. Key concepts include calculating equivalent resistance and current distribution. After the switch is opened, the video outlines how to redraw the circuit and determine the time constant, ultimately presenting the equation for current as a function of time. This educational guide emphasizes the methodology for understanding RL circuit behavior and the exponential decay of current in inductors.

Takeaways

• 🔌 An RL circuit consists of a resistor (R) and an inductor (L), which impacts how current flows when the switch is opened.
• 🔄 Before the switch opens (time < 0), the inductor behaves like a short circuit, allowing maximum current to flow through it.
• ⚖️ The equivalent resistance of resistors in parallel can be calculated using the formula: R_eq = (R1 * R2) / (R1 + R2).
• 📏 Total resistance in the circuit is determined by combining the equivalent resistance with any series resistances.
• ⚡ The initial current through the circuit before opening the switch can be calculated using Ohm's law: I = V / R.
• 🔍 Current distribution through parallel resistors can be determined by the ratio of their resistances.
• ⏳ After the switch opens (time ≥ 0), the inductor initially maintains the same current, which is essential for understanding circuit dynamics.
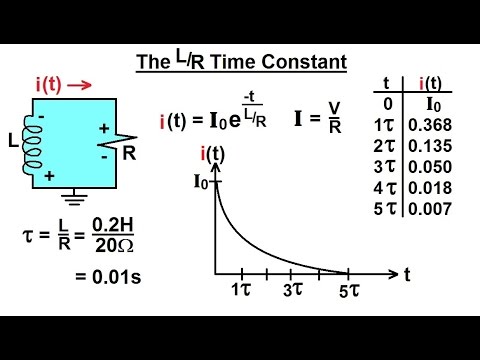
• 📉 The time constant (τ) of an RL circuit is calculated as τ = L / R_eq, indicating how quickly current changes over time.
• 📊 The current through the inductor over time follows an exponential decay pattern, represented by the formula: I(t) = I_initial * e^(-t/τ).
• 🛠️ Understanding these principles is crucial for analyzing RL circuits in electronics, particularly in predicting current behavior during switching events.

Q & A

What is the initial condition of the RL circuit before the switch is opened?

Before the switch is opened, the inductor acts as a short circuit, allowing the entire current to flow through it while the 16-ohm resistor is effectively removed from the circuit.

How do you determine the equivalent resistance of the parallel resistors in the circuit?

The equivalent resistance of the two resistors in parallel is calculated using the formula: R_eq = (R1 * R2) / (R1 + R2). For the 12-ohm and 4-ohm resistors, R_eq equals 3 ohms.

What is the total resistance in the circuit with the 10-volt source before the switch opens?

The total resistance in the circuit is the sum of the 2-ohm resistor and the equivalent resistance of the parallel combination of the 12-ohm and 4-ohm resistors, which totals 5 ohms.

How is the initial current through the circuit calculated?

The initial current is calculated using Ohm's Law, I = V / R. For the 10-volt source and 5-ohm resistance, the initial current is 2 amps.

What portion of the initial current flows through the 4-ohm resistor?

The current through the 4-ohm resistor is 1.5 amps, calculated as I_4 = I * (R_12 / (R_4 + R_12)), where I is the initial current.

What happens to the circuit at time equals zero when the switch is opened?

When the switch is opened, the inductor retains the initial current of 1.5 amps, and the circuit is redrawn to show only the components that remain active.

What is the equivalent resistance after the switch is opened?

After the switch is opened, the two 16-ohm resistors in parallel combine to form an equivalent resistance of 8 ohms.

How is the time constant of the RL circuit calculated?

The time constant τ is calculated as the inductance divided by the equivalent resistance. For this circuit, τ = 2 H / 8 ohms = 0.25 seconds.

What is the equation for the current through the inductor as a function of time?

The equation for the current through the inductor is given by I(t) = I_initial * e^(-t/τ). For this case, it simplifies to I(t) = 1.5 * e^(-4t).

What does the term 'time constant' signify in the context of an RL circuit?

The time constant indicates the rate at which current through the inductor will decrease after the switch is opened, reflecting the time it takes for the current to decay to about 37% of its initial value.