3.1 Functions
Summary
TLDRThis video lesson introduces the concept of functions in mathematics, focusing on the vertical line test to determine whether a graph represents a function. Viewers learn about the definitions of domain and range, with domain as the input values (x-coordinates) and range as the output values (y-coordinates). The lesson includes examples, emphasizes the difference between independent and dependent variables, and illustrates how to find domain and range from graphs. Finally, an input/output table is created using the equation y = -2x + 3, demonstrating how to calculate outputs based on given inputs.
Takeaways
- 😀 A function is defined by its ability to pass the vertical line test on a graph.
- 📊 If a vertical line intersects the graph at more than one point, it is not a function.
- ✏️ The domain refers to the input values (x-coordinates) of a function.
- 📈 The range refers to the output values (y-coordinates) of a function.
- 🔄 The independent variable is the domain (x), while the dependent variable is the range (y).
- 📝 To find the domain and range, identify the relevant x and y values from the graph.
- 📏 For continuous functions, use inequalities to express the domain and range.
- 🔍 Discrete points in the domain can be explicitly listed (e.g., -3, -1, 1, 3).
- ⚙️ Example calculation: For the function y = -2x + 3, calculate outputs for various inputs.
- 📉 The outputs for y = -2x + 3 decrease consistently as the inputs increase.
Q & A
What is the vertical line test and how does it determine if a graph represents a function?
-The vertical line test is a method used to determine if a graph represents a function. If a vertical line intersects the graph at only one point, then the graph represents a function. If the vertical line intersects at two or more points, it does not represent a function.
What is the difference between domain and range in a function?
-The domain of a function refers to the set of input values (x-coordinates), while the range refers to the set of output values (y-coordinates).
What are independent and dependent variables in the context of functions?
-In a function, the independent variable is typically the input (x), which does not depend on other variables. The dependent variable is the output (y), which depends on the value of the independent variable.
How can you find the domain and range of a graph with discrete points?
-To find the domain and range from a graph with discrete points, identify the x-coordinates for the domain and the y-coordinates for the range based on the points plotted on the graph.
What is a compound inequality, and how is it used to express domain and range?
-A compound inequality is a mathematical expression that describes a range of values between two points. It is used to represent the domain and range when the values are continuous. For example, the domain can be expressed as 'a ≤ x ≤ b' and the range as 'c ≤ y ≤ d'.
How do you calculate the outputs for a function using an input/output table?
-To calculate the outputs for a function using an input/output table, substitute the input values into the function's equation to find the corresponding output values. Each input produces a specific output based on the function.
In the provided function y = -2x + 3, what are the outputs for the inputs -2, 0, 2, and 4?
-For the function y = -2x + 3: - When x = -2, y = 7 - When x = 0, y = 3 - When x = 2, y = -1 - When x = 4, y = -5.
Why is it important to distinguish between discrete and continuous data when analyzing functions?
-Distinguishing between discrete and continuous data is important because it affects how you represent the domain and range. Discrete data is represented with specific points, while continuous data is represented with intervals.
What should you do if a graph does not pass the vertical line test?
-If a graph does not pass the vertical line test, it indicates that the graph does not represent a function, meaning there are multiple outputs (y-values) for at least one input (x-value).
What are some examples of functions that pass the vertical line test?
-Examples of functions that pass the vertical line test include linear functions (like y = 2x + 1), quadratic functions (like y = x^2), and exponential functions (like y = e^x), as they only intersect any vertical line at one point.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Introduction to Functions (2 of 2: Examples & Counter-Examples)

Relations & Functions
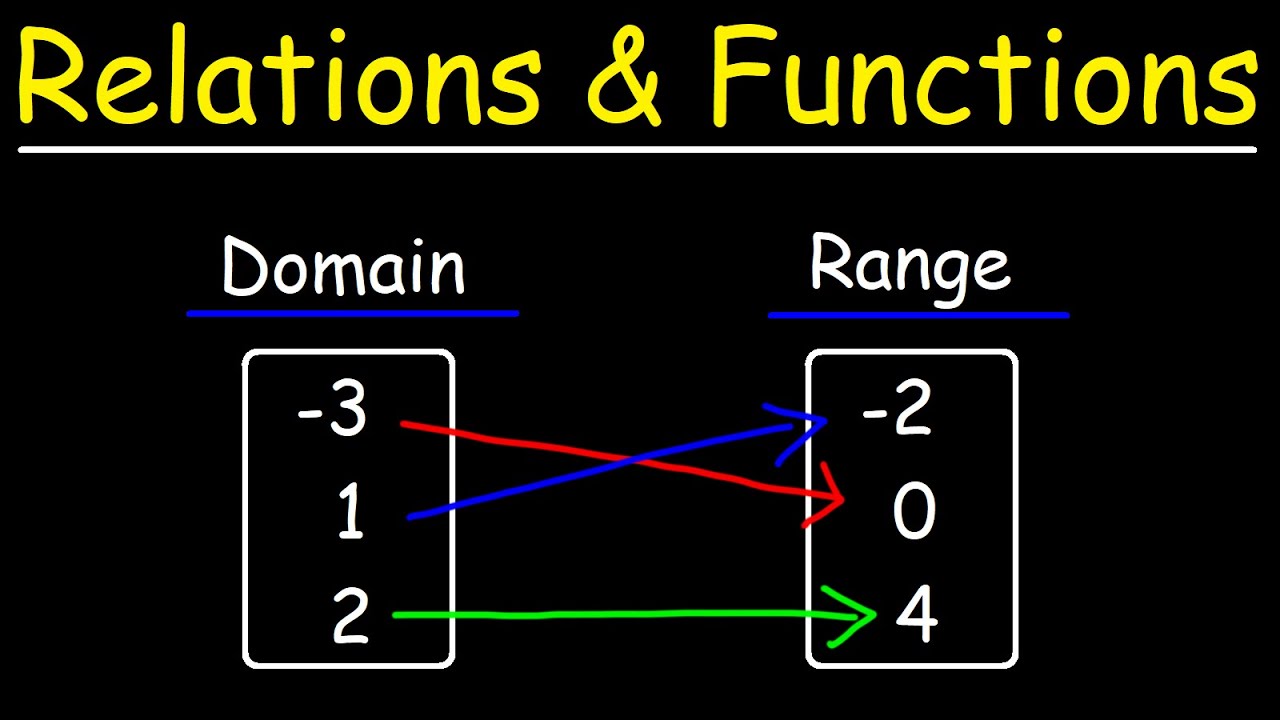
Relations and Functions | Algebra

REPRESENTATION OF FUNCTIONS ┃Grade 11 General Mathematics

MCR3U (1.1) - Relations vs Functions - Grade 11 Functions
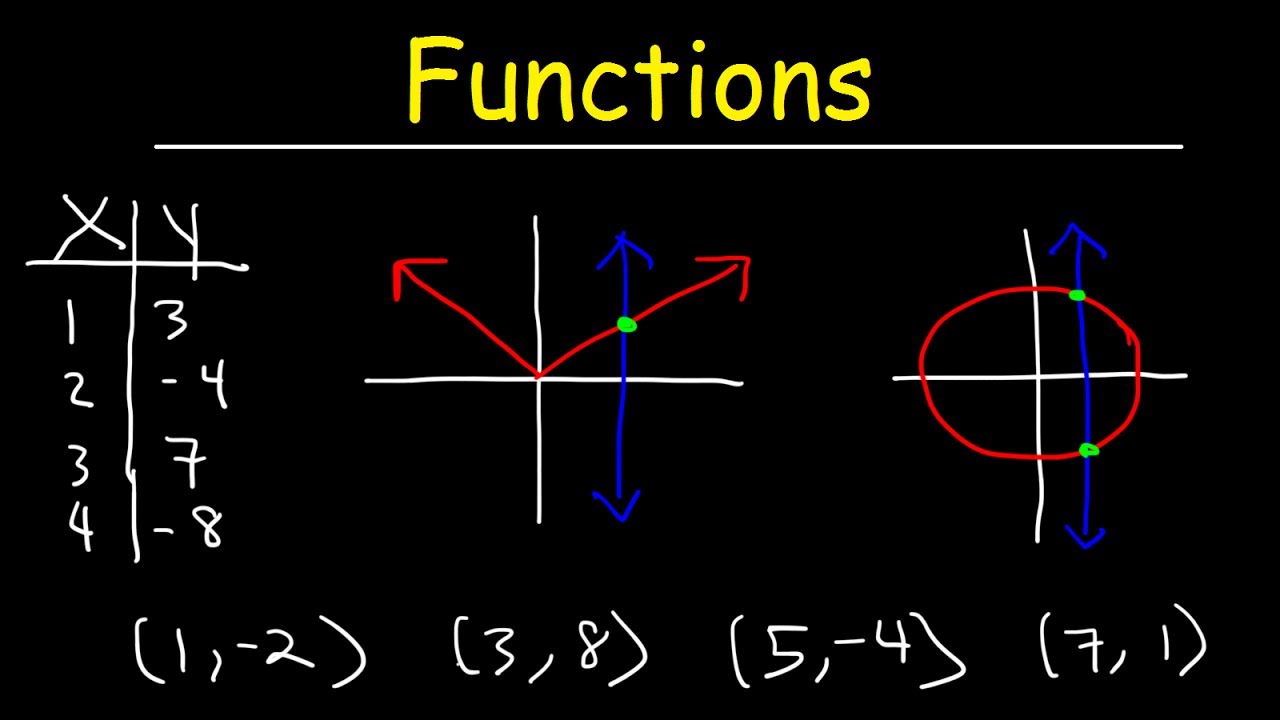
Functions - Vertical Line Test, Ordered Pairs, Tables, Domain and Range
5.0 / 5 (0 votes)
