2D Elasticity – 1: Plane Stress
Summary
TLDRIn this lecture on 2D elasticity, the instructor explores the concepts of plane stress and plane strain, emphasizing their significance in simplifying complex three-dimensional engineering problems. The discussion outlines key considerations, including geometric setups, stress components, and loading conditions. The Airy stress function approach is introduced as a method to satisfy stress equilibrium equations through a scalar function, ensuring compatibility of strain fields. Caution is advised in selecting the function to avoid incompatible displacement results. The lecture sets the stage for deeper exploration of compatibility equations in subsequent sessions.
Takeaways
- 📚 2D elasticity can simplify complex 3D problems, making it essential for practical engineering applications.
- 🔍 Plane stress and plane strain are two critical concepts that help reduce 3D elasticity problems to 2D.
- 📏 Plane stress conditions are applicable to very thin plates bounded by parallel stress-free planes.
- 🚫 Under plane stress, certain stress components (σ_z, σ_zx, σ_yz) can be approximated to zero due to negligible thickness.
- 🧮 Non-zero stress components (σ_xx, σ_yy, σ_xy) depend solely on the x and y coordinates, simplifying calculations.
- 🌐 The absence of body forces in the z direction is necessary to maintain stress independence from the z-axis.
- 📐 The Airy stress function, introduced by A. C. Airy, provides a mathematical framework to satisfy stress equilibrium equations.
- ⚖️ The choice of the Airy stress function must ensure compatibility of strain fields to avoid unrealistic results.
- 🔄 The mathematical forms used in the Airy stress function approach need to incorporate compatibility equations for accurate modeling.
- 🔜 The next lecture will delve deeper into embedding compatibility equations within the Airy stress function framework.
Q & A
What is the primary focus of the lecture discussed in the transcript?
-The lecture primarily focuses on the topic of 2D elasticity, specifically discussing concepts of plane stress and plane strain.
Why is it relevant to revisit 2D elasticity after studying 3D elasticity?
-Revisiting 2D elasticity is relevant because many practical engineering problems, despite being inherently three-dimensional, can be effectively simplified and analyzed using 2D elasticity models.
What are the two primary conditions discussed in the context of 2D elasticity?
-The two primary conditions are 'plane stress' and 'plane strain,' which are essential for simplifying three-dimensional stress and strain analyses.
What is a canonical example of plane stress mentioned in the lecture?
-A canonical example of plane stress is a very thin plate, where the thickness is small compared to the other dimensions.
What condition is specified for the stress components at the boundaries of the thin plate?
-The stress components at the boundaries, specifically at z equal to plus and minus h, are stated to be stress-free, meaning that the normal and shear stresses in the z-direction are zero.
How are the stress components approximated in the thin plate under plane stress conditions?
-In plane stress conditions, the stress components sigma_z, sigma_zx, and sigma_yz are approximated to be zero due to the thinness of the plate, while the other components depend only on x and y.
What is the significance of the Airy stress function approach mentioned in the lecture?
-The Airy stress function approach allows for the formulation of stress components in a way that satisfies the equilibrium equations, providing a method for solving problems in elasticity.
What is a potential issue when choosing the Airy stress function?
-A potential issue is that an arbitrary choice of the Airy stress function may lead to incompatible strain fields, which could result in unphysical solutions.
What measures are suggested to ensure the chosen Airy stress function results in compatible strain fields?
-To ensure compatibility, the approach includes embedding the compatibility equations within the mathematical framework of the Airy stress function.
What will be the focus of the next part of the lecture as indicated in the transcript?
-The next part of the lecture will focus on including the compatibility equations in the Airy stress function approach and proceeding further with the analysis.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Understanding Plane Stress
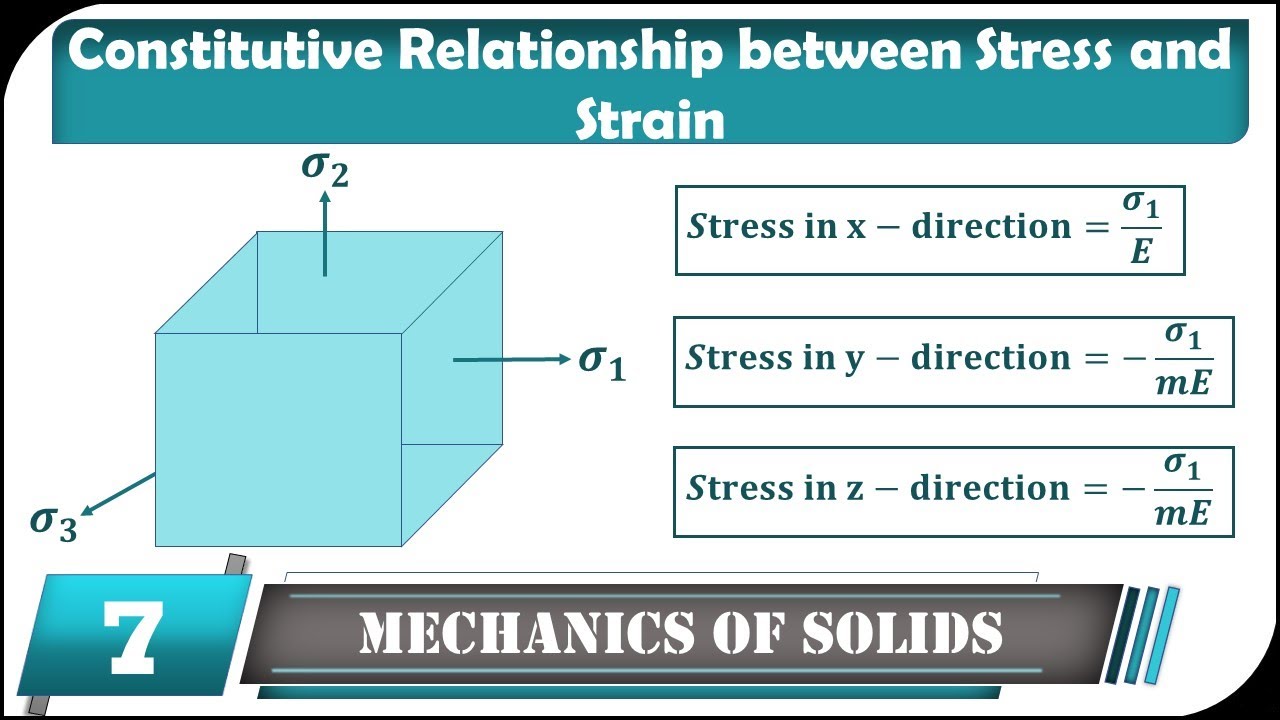
Constitutive Relationship between Stress and Strain | Mechanics of Solid / Engineering Mechanics
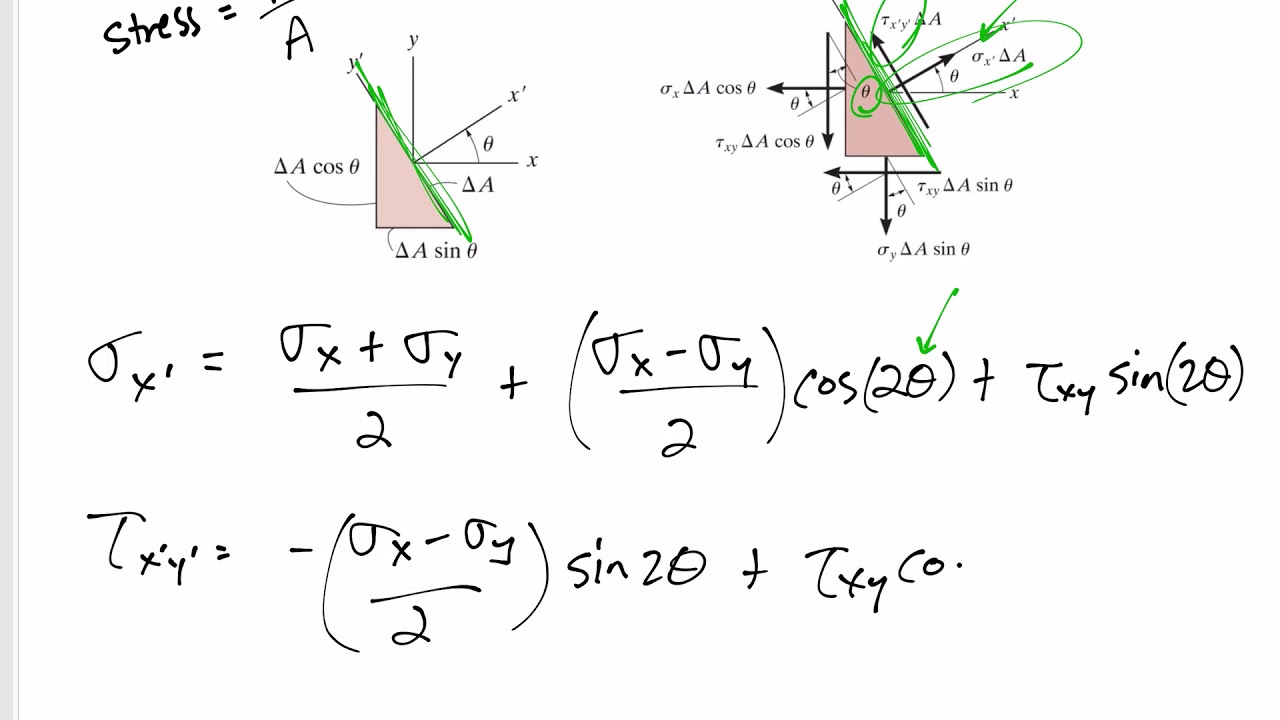
Mechanics of Materials - 2D Plane stress transformation equations
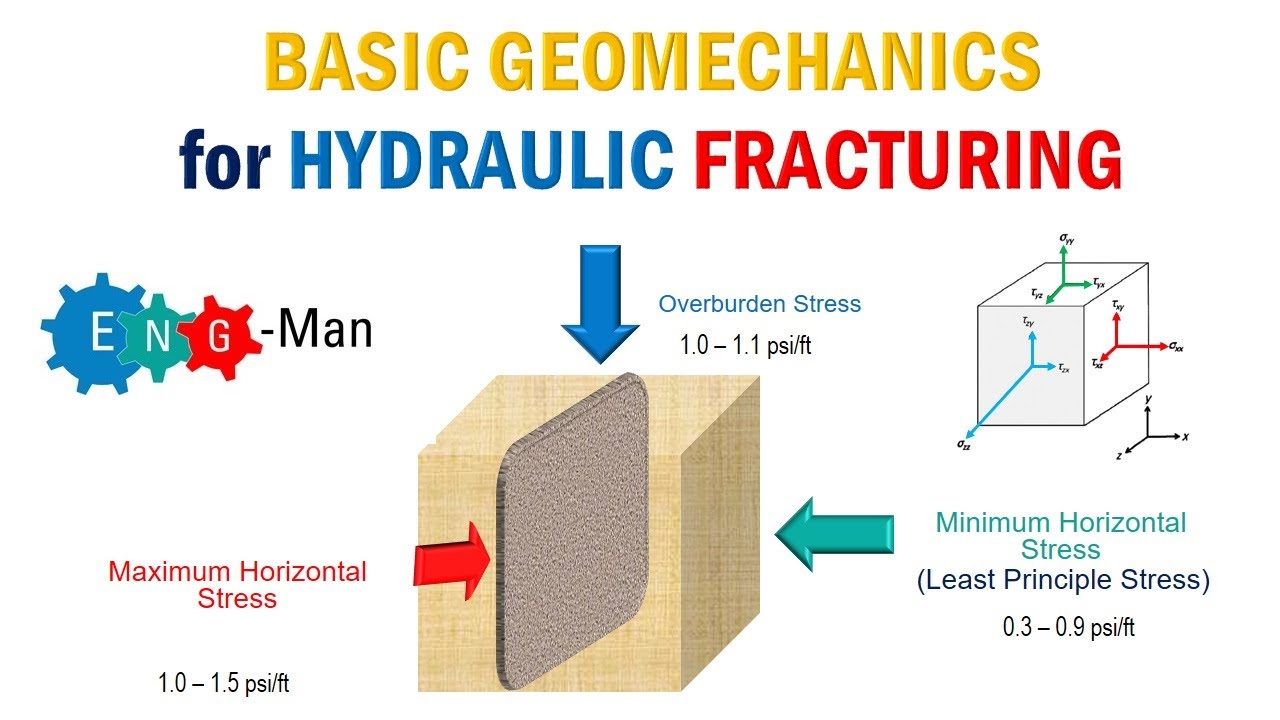
Basic Geomechanics for Hydraulic Fracturing

Reaching Breaking Point: Materials, Stresses, & Toughness: Crash Course Engineering #18
Stress and Strain | Stress strain curve of mild steel | Mechanical Properties of Solids |
5.0 / 5 (0 votes)
