SISTEMAS DE ECUACIONES - LOS 3 MÉTODOS EXPLICADOS!
Summary
TLDREn este video, se explica de manera clara cómo resolver un sistema de ecuaciones utilizando tres métodos principales: sustitución, reducción (eliminación) e igualación. Se presentan ejemplos detallados de cada método, mostrando cómo despejar variables, eliminar términos y resolver las ecuaciones para encontrar los valores de las incógnitas. A través de estos métodos, los estudiantes pueden comprender diferentes enfoques para llegar a la misma solución, mejorando su habilidad para manejar sistemas de ecuaciones en álgebra.
Takeaways
- 😀 Se presentan los métodos de resolución de sistemas de ecuaciones: sustitución, reducción e igualación.
- 😀 El método de sustitución implica despejar una variable y sustituir su valor en otra ecuación.
- 😀 En el ejemplo dado, se trabaja con el sistema de ecuaciones 5x - 3y = 11 y 4x + y = 2.
- 😀 Se realizan operaciones algebraicas para obtener los valores de las variables en el sistema.
- 😀 El método de reducción consiste en sumar o restar ecuaciones para eliminar una variable.
- 😀 Se demuestra que la solución de los sistemas de ecuaciones puede ser verificada al sustituir los valores obtenidos.
- 😀 En el método de igualación, se despejan las variables en ambas ecuaciones y se igualan las expresiones.
- 😀 Se enfatiza la importancia de tener un denominador común para facilitar la suma de fracciones en las ecuaciones.
- 😀 Se muestra cómo todos los métodos conducen a los mismos resultados en diferentes etapas del proceso.
- 😀 El conocimiento de estos métodos es esencial para resolver problemas matemáticos de manera eficiente.
Q & A
¿Qué son los sistemas de ecuaciones?
-Los sistemas de ecuaciones son conjuntos de dos o más ecuaciones que comparten variables comunes y que se resuelven simultáneamente.
¿Cuáles son los métodos utilizados para resolver sistemas de ecuaciones mencionados en el video?
-Los métodos mencionados son el método de sustitución, el método de reducción y el método de igualación.
¿Cómo funciona el método de sustitución?
-El método de sustitución implica despejar una variable en una de las ecuaciones y luego sustituir esa expresión en la otra ecuación.
¿Qué pasos se deben seguir en el método de reducción?
-En el método de reducción, se suman o restan las ecuaciones de manera que se elimine una variable, permitiendo resolver por la otra.
¿Cuál es el enfoque del método de igualación?
-El método de igualación consiste en despejar la misma variable en ambas ecuaciones y luego igualar las expresiones resultantes.
¿Qué ejemplos de ecuaciones se utilizaron en el video?
-Se utilizaron las ecuaciones 5x - 3y = 11 y 4x + y = 2 como ejemplos para ilustrar los métodos.
¿Por qué es importante tener un denominador común en algunos casos?
-Tener un denominador común facilita la suma o resta de fracciones, lo que es esencial para resolver las ecuaciones correctamente.
¿Qué se debe hacer si una variable se despeja como negativo?
-Si una variable se despeja como negativa, se puede considerar al resolver y realizar las operaciones correspondientes para obtener la solución positiva si es necesario.
¿Cuáles son los resultados de aplicar los tres métodos en el ejemplo dado?
-Los tres métodos llevan a la misma solución para las variables, lo que muestra la consistencia de los métodos de resolución de sistemas de ecuaciones.
¿Cómo se relacionan estos métodos con la resolución de problemas reales?
-Estos métodos se aplican en diversas áreas como la economía, la ingeniería y la ciencia, donde se necesita resolver problemas que involucran múltiples variables interrelacionadas.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

4 Métodos en 5 minutos para resolver sistema de ecuaciones lineales 2x2

✅ Sistema de Ecuaciones Lineales [ Método de Sustitución ] - Ejemplos Resueltos #1

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción
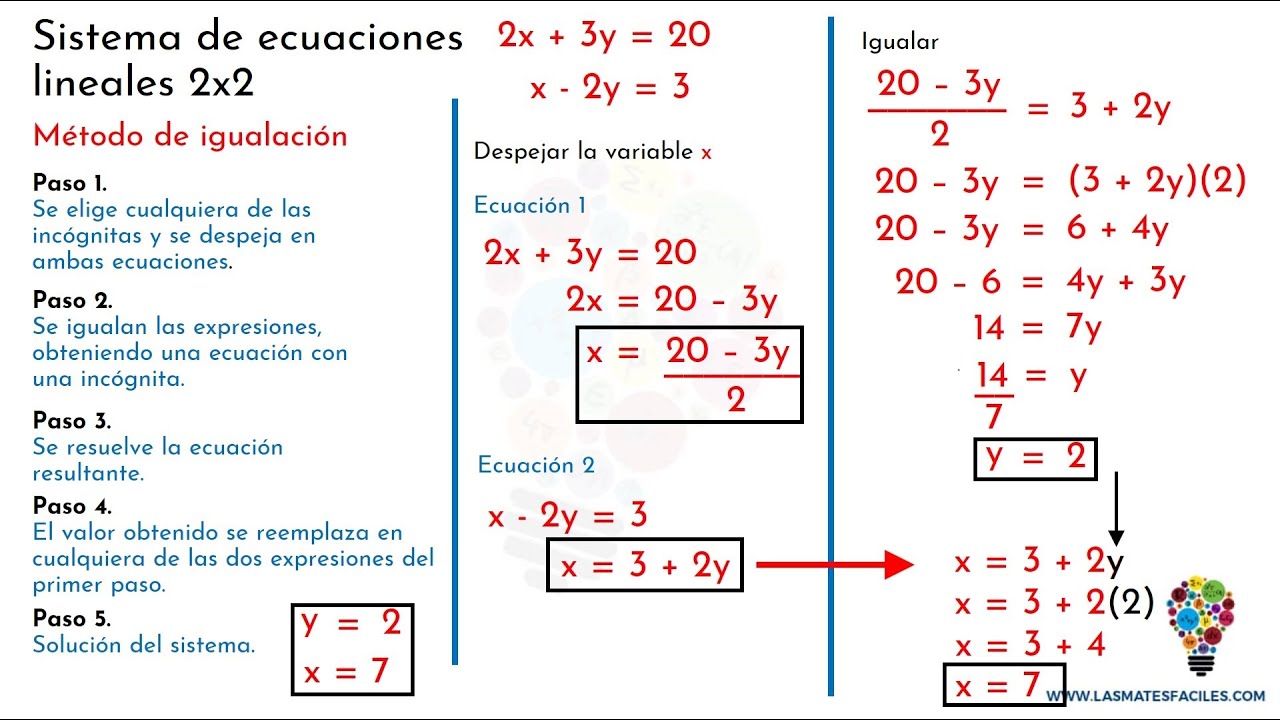
Sistemas de Ecuaciones 2x2 - Método de Igualación

PLANTEAR Y RESOLVER ECUACIONES 2 x 2 super fácil - para principiantes
5.0 / 5 (0 votes)
