Angles formed by parallel lines and transversals | Geometry | Khan Academy
Summary
TLDRThis video explains the concept of parallel lines and their relationship with angles formed by a transversal line. It defines parallel lines as those that never intersect and shares that they have the same slope but different y-intercepts. The script illustrates how angles at the intersections are equal, emphasizing vertical angles and corresponding angles, while introducing terms like 'alternate interior angles.' Ultimately, the video aims to clarify these geometric relationships in an intuitive manner, reinforcing the idea that understanding these angles is essential in geometry.
Takeaways
- 😀 Lines that never intersect and are on the same plane are called parallel lines.
- 📏 Parallel lines have the same slope but different y-intercepts.
- 🔀 A transversal is a line that intersects two or more lines in the same plane.
- 🔺 Vertical angles formed by the intersection of a transversal and parallel lines are equal.
- 📐 Corresponding angles at the intersection of a transversal and parallel lines are also equal.
- 🔄 The concept of corresponding angles helps visualize the relationship between angles in a transversal configuration.
- ⚖️ Alternate interior angles, formed on opposite sides of the transversal, are equal when lines are parallel.
- 📈 Understanding angles formed by parallel lines and transversals is essential in geometry.
- 🧮 Labeling angles with letters aids in understanding relationships and equivalences between them.
- 🔍 The intuitive nature of angle relationships between parallel lines and transversals is often evident without formal proof.
Q & A
What defines parallel lines?
-Parallel lines are lines that lie on the same plane and never intersect, maintaining the same slope but differing in y-intercepts.
What is a transversal in geometry?
-A transversal is a line that intersects two or more lines. In this context, it intersects two parallel lines.
How can we visually identify parallel lines in a diagram?
-Parallel lines can be identified in diagrams by the presence of arrows drawn on the lines, indicating they are parallel.
What are vertical angles, and how do they relate to parallel lines?
-Vertical angles are the angles opposite each other at the intersection of two lines. They are always equal, regardless of whether the lines are parallel.
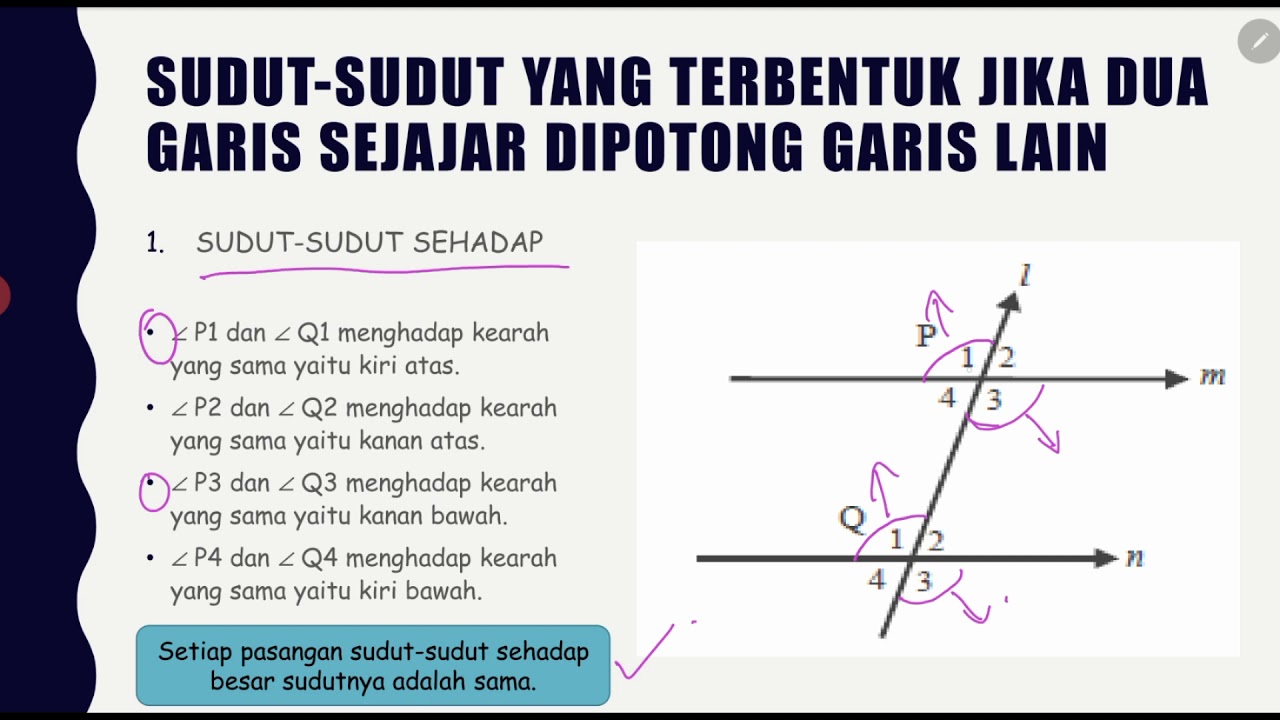
What are corresponding angles, and how are they defined when a transversal intersects parallel lines?
-Corresponding angles are angles that occupy the same relative position at each intersection of the transversal with the parallel lines. These angles are equal when the lines are parallel.
What are alternate interior angles, and what is their significance?
-Alternate interior angles are angles located between two parallel lines on opposite sides of the transversal. They are equal in measure when the lines are parallel.
What relationship can be established between the angles formed when a transversal crosses two parallel lines?
-When a transversal crosses parallel lines, vertical angles are equal, corresponding angles are equal, and alternate interior angles are equal.
How can you prove that corresponding angles are equal using a protractor?
-By placing a protractor at the intersection of the transversal and one parallel line, you can measure the angle formed. If you do the same at the other intersection, the corresponding angle will measure the same.
What happens to the angles if you tilt the transversal?
-Tilting the transversal does not change the relationships between the angles; corresponding angles will remain equal, and vertical angles will still be equal.
Why is it said that the relationships between these angles are 'intuitively obvious'?
-The relationships are considered intuitively obvious because, upon visual inspection or measurement, one can readily see the equality between the angles formed at the intersections.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

HUBUNGAN SUDUT-SUDUT PADA DUA GARIS SEJAJAR YANG DIPOTONG OLEH SATU GARIS

Sudut pada Dua Garis Sejajar Kelas 7

Sudut yang terjadi jika Dua Garis Sejajar dipotong oleh Sebuah Garis

ÂNGULOS CORRESPONDENTES | ÂNGULOS FORMADOS POR RETAS PARALELAS CORTADAS POR UMA TRANSVERSAL|

Kupas Tuntas Sudut dan Garis (Sehadap, Bertolak belakang, dalam berseberangan dll)
Kedudukan Dua Garis & Hubungan Antara Sudut dan Garis Kelas 7 SMP
5.0 / 5 (0 votes)
