Multiplicación de matrices - Producto de matrices 2x2 | Ejemplo 2
Summary
TLDREl video es una lección sobre cómo multiplicar matrices de 2x2. El instructor explica paso a paso cómo realizar la multiplicación de dos matrices cuadradas, destacando la obtención de los cuatro elementos de la matriz resultante (c11, c12, c21 y c22). Se multiplica la primera fila de la primera matriz por las columnas de la segunda, explicando los signos en la multiplicación y la suma de los resultados. Al final, se proporciona un ejercicio para practicar, motivando a los espectadores a suscribirse y seguir el curso completo.
Takeaways
- 📘 El video trata sobre cómo multiplicar matrices de 2x2.
- 🧮 Se enfatiza que la multiplicación de dos matrices cuadradas produce otra matriz cuadrada del mismo tamaño.
- 📺 Se recomienda ver un video anterior que explica la multiplicación de matrices paso a paso.
- ✍️ El presentador sugiere pausar el video para resolver el ejercicio y luego comparar los resultados.
- 📝 Se utilizan notaciones específicas para identificar cada elemento de la matriz resultante, como c11, c12, c21 y c22.
- 🔄 Se explica el procedimiento para calcular cada elemento de la matriz multiplicando las filas de la primera matriz por las columnas de la segunda.
- ➖ Se realiza el cálculo de cada elemento individualmente, teniendo en cuenta las reglas de multiplicación y suma de matrices.
- ✅ El presentador revisa los cálculos para asegurarse de que los elementos de la matriz sean correctos.
- 🧩 Se propone un ejercicio para que los espectadores practiquen la multiplicación de matrices.
- 👍 Se invita a los espectadores a suscribirse, comentar y compartir el video para acceder a más contenido educativo.
Q & A
¿Qué se enseña en este video?
-El video enseña cómo multiplicar dos matrices de 2x2, explicando el proceso paso a paso.
¿Cuáles son los elementos de una matriz 2x2?
-Los elementos de una matriz 2x2 son cuatro: c11, c12, c21, y c22, que representan las posiciones en la primera y segunda fila, y la primera y segunda columna.
¿Cómo se calcula el elemento c11 de la matriz resultante?
-El elemento c11 se calcula multiplicando la primera fila de la primera matriz por la primera columna de la segunda matriz, sumando los productos individuales.
¿Qué operación se realiza entre los productos individuales en la multiplicación de matrices?
-Se suman los productos individuales obtenidos de la multiplicación de los elementos correspondientes de las filas y columnas.
¿Qué es el valor de c11 en el primer ejemplo del video?
-El valor de c11 en el primer ejemplo es -39, obtenido al multiplicar -5 por 9 (que da -45) y 3 por 2 (que da 6), y luego sumarlos.
¿Cómo se obtiene el valor de c12?
-El valor de c12 se obtiene multiplicando la primera fila de la primera matriz por la segunda columna de la segunda matriz. En el ejemplo, el resultado es -15.
¿Qué valor tiene el elemento c21 en el primer ejemplo?
-El valor de c21 es 50, obtenido al multiplicar la segunda fila de la primera matriz por la primera columna de la segunda matriz.
¿Cómo se calcula el elemento c22?
-El elemento c22 se calcula multiplicando la segunda fila de la primera matriz por la segunda columna de la segunda matriz. En el ejemplo, el resultado es -35.
¿Cuál es el propósito del ejercicio final presentado en el video?
-El ejercicio final se presenta como una práctica para que los espectadores puedan aplicar el proceso de multiplicación de matrices que se explicó en el video.
¿Qué se recomienda hacer si los espectadores necesitan más claridad sobre el proceso de multiplicación de matrices?
-Se recomienda que los espectadores vean el video anterior, donde se explicó el proceso de multiplicación de matrices en más detalle.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
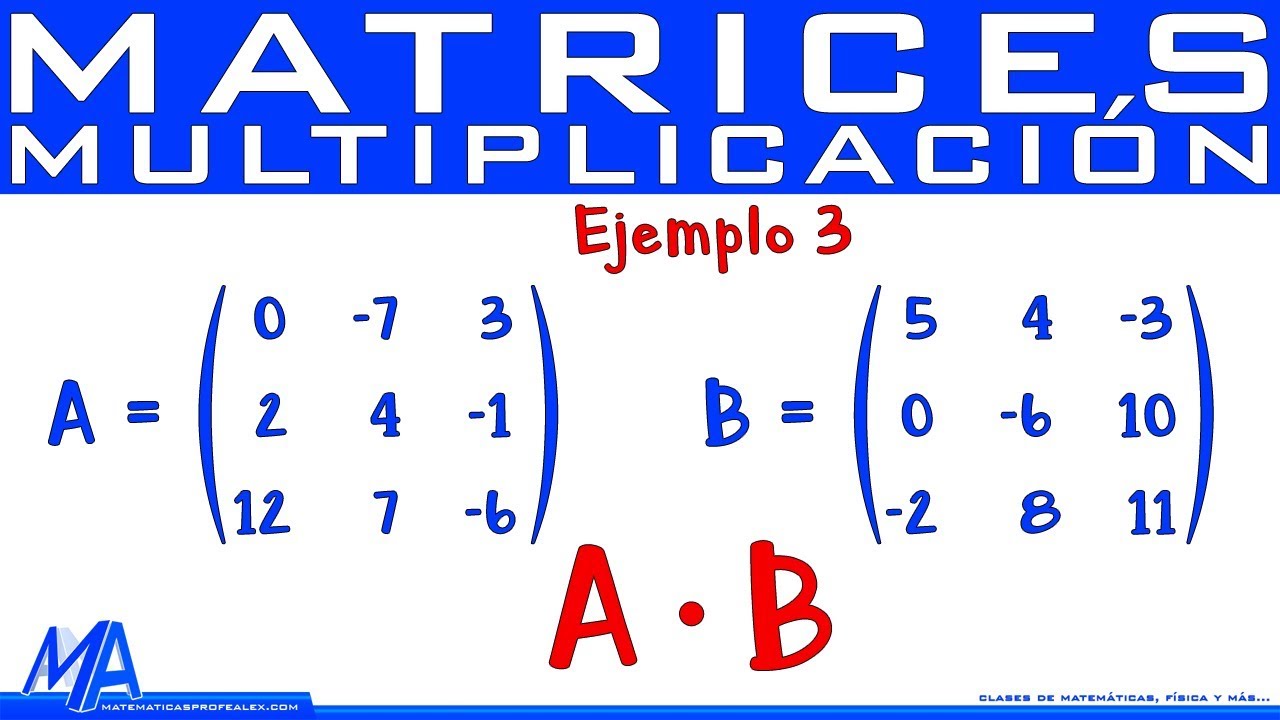
Multiplicación de matrices - Producto de matrices 3x3 | Ejemplo 3

📢 ESPACIOS VECTORIALES de MATRICES💥 Bases y coordenadas. Álgebra Lineal #matematicas

RESOLVER SISTEMAS DE ECUACIONES MÉTODO DE REDUCCIÓN O SUMA Y RESTA Super fácil - Para principiantes

✅ Sistema de Ecuaciones Lineales [ Método de Eliminación ] - Ejemplos Resueltos #1

BASE de un ESPACIO VECTORIAL Ejercicios RESUELTOS Álgebra Lineal

MULTIPLICACIÓN y DIVISIÓN de NÚMEROS ENTEROS | REGLA de los SIGNOS | SUPER FÁCIL 🤩 | Parte 2
5.0 / 5 (0 votes)
