SYMMETRIE von Funktionen untersuchen – Achsensymmetrie und Punktsymmetrie berechnen
Summary
TLDRIn diesem Video wird erklärt, wie man rechnerisch überprüft, ob eine Funktion achsensymmetrisch oder punktsymmetrisch ist. Dabei werden die jeweiligen Formeln und Vorgehensweisen vorgestellt, die diese Symmetrien definieren. Es wird gezeigt, wie man eine Vermutung über die Symmetrie der Funktion anstellt, um unnötige Berechnungen zu vermeiden. Durch Beispiele wird die Vorgehensweise schrittweise demonstriert: Von der Substitution von -x in die Funktion bis zur Vereinfachung der Terme. Auch wird erklärt, wie ungerade und gerade Exponenten die Symmetrie beeinflussen. Der Fokus liegt auf der rechnerischen Bestätigung der Symmetrie ohne den Graphen der Funktion zu kennen.
Takeaways
- 😀 Eine Funktion ist achsensymmetrisch, wenn f(x) = f(-x) gilt.
- 🧐 Um zu überprüfen, ob eine Funktion symmetrisch ist, kann man rechnerisch f(-x) bilden und mit f(x) vergleichen.
- 🔄 Bei einer achsensymmetrischen Funktion sind alle Exponenten der Terme gerade.
- ❗ Wenn weder Achsen- noch Punktsymmetrie vorliegt, liegt keine einfache Symmetrie vor.
- 🧮 Bei Polynomen weisen gerade Exponenten auf Achsensymmetrie hin, während ungerade Exponenten Punktsymmetrie anzeigen.
- 💡 Bei Punktspiegelung gilt: f(-x) = -f(x).
- 📐 Gerade Exponenten machen das Minuszeichen vor der Variablen positiv, daher entfällt es in der Berechnung.
- ❓ Bei ungeraden Exponenten bleibt das Minuszeichen erhalten und beeinflusst das Vorzeichen des Ergebnisses.
- 🔍 Falls weder Achsen- noch Punktsymmetrie vorliegt, müssen beide Formen getestet werden.
- 📊 Trigonometrische Funktionen wie der Sinus können auch auf Punktsymmetrie überprüft werden, da sie spezielle Symmetrieeigenschaften aufweisen.
Q & A
Wie erkennt man, ob eine Funktion achsensymmetrisch ist?
-Eine Funktion ist achsensymmetrisch, wenn für sie gilt: f(x) = f(-x). Das bedeutet, dass die Funktion den gleichen Wert für x und -x hat, was sich in einer Symmetrie zur y-Achse zeigt.
Was ist der Unterschied zwischen Achsen- und Punktsymmetrie bei Funktionen?
-Der Unterschied liegt in der Bedingung, die die Funktion erfüllen muss. Bei Achsensymmetrie gilt f(x) = f(-x), während bei Punktsymmetrie die Bedingung f(-x) = -f(x) erfüllt sein muss. Achsensymmetrische Funktionen sind zur y-Achse gespiegelt, punktsymmetrische Funktionen sind bezüglich des Ursprungs gespiegelt.
Was ist ein Indiz für Achsensymmetrie bei einer Funktion?
-Ein Indiz für Achsensymmetrie ist, wenn alle Exponenten der Variablen in der Funktion gerade sind, einschließlich des konstanten Terms. Zum Beispiel, wenn in einem Polynom nur gerade Potenzen vorkommen, ist die Funktion achsensymmetrisch.
Warum reicht es oft, nur die Exponenten zu überprüfen, um Symmetrie zu erkennen?
-Bei Polynomen reicht es oft, nur die Exponenten zu überprüfen, weil gerade Exponenten für Achsensymmetrie und ungerade Exponenten für Punktsymmetrie sorgen. Dies ist eine praktische Methode, um eine Vermutung über die Symmetrie der Funktion anzustellen, ohne aufwendige Rechnungen durchzuführen.
Wie zeigt man rechnerisch, dass eine Funktion achsensymmetrisch ist?
-Um rechnerisch zu zeigen, dass eine Funktion achsensymmetrisch ist, bildet man f(-x) und überprüft, ob das Ergebnis mit f(x) identisch ist. Falls das der Fall ist, ist die Funktion achsensymmetrisch.
Wie zeigt man rechnerisch, dass eine Funktion punktsymmetrisch ist?
-Um Punktsymmetrie zu zeigen, bildet man f(-x) und überprüft, ob f(-x) = -f(x) gilt. Wenn das der Fall ist, ist die Funktion punktsymmetrisch.
Warum bleibt bei ungeraden Potenzen das Minuszeichen erhalten?
-Bei ungeraden Potenzen bleibt das Minuszeichen erhalten, weil (-x)^ungerade = -x^ungerade ist. Dies führt dazu, dass der Vorzeichenwechsel durch die Potenzierung nicht aufgehoben wird.
Was passiert bei geraden Potenzen von -x?
-Bei geraden Potenzen verschwindet das Minuszeichen, da (-x)^gerade = x^gerade ist. Das Minuszeichen wird durch die gerade Potenz neutralisiert.
Warum ist es wichtig, zwischen Achsen- und Punktsymmetrie zu unterscheiden?
-Es ist wichtig, zwischen Achsen- und Punktsymmetrie zu unterscheiden, weil beide unterschiedliche geometrische Eigenschaften der Funktion beschreiben und unterschiedliche Bedingungen erfüllen müssen. Achsensymmetrische Funktionen sind zur y-Achse symmetrisch, während punktsymmetrische Funktionen um den Ursprung gespiegelt sind.
Was bedeutet es, wenn eine Funktion weder achsen- noch punktsymmetrisch ist?
-Wenn eine Funktion weder achsen- noch punktsymmetrisch ist, bedeutet das, dass sie keine einfache Symmetrie aufweist. In diesem Fall gibt es keine Spiegelung an der y-Achse oder am Ursprung, die für die Funktion gilt.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Notwendige und Hinreichende Bedingung ?häää!!! Kurvendiskussion Übersicht - simplexy.de
Ping im Netzwerk: Überprüfen ob Rechner erreichbar sind!
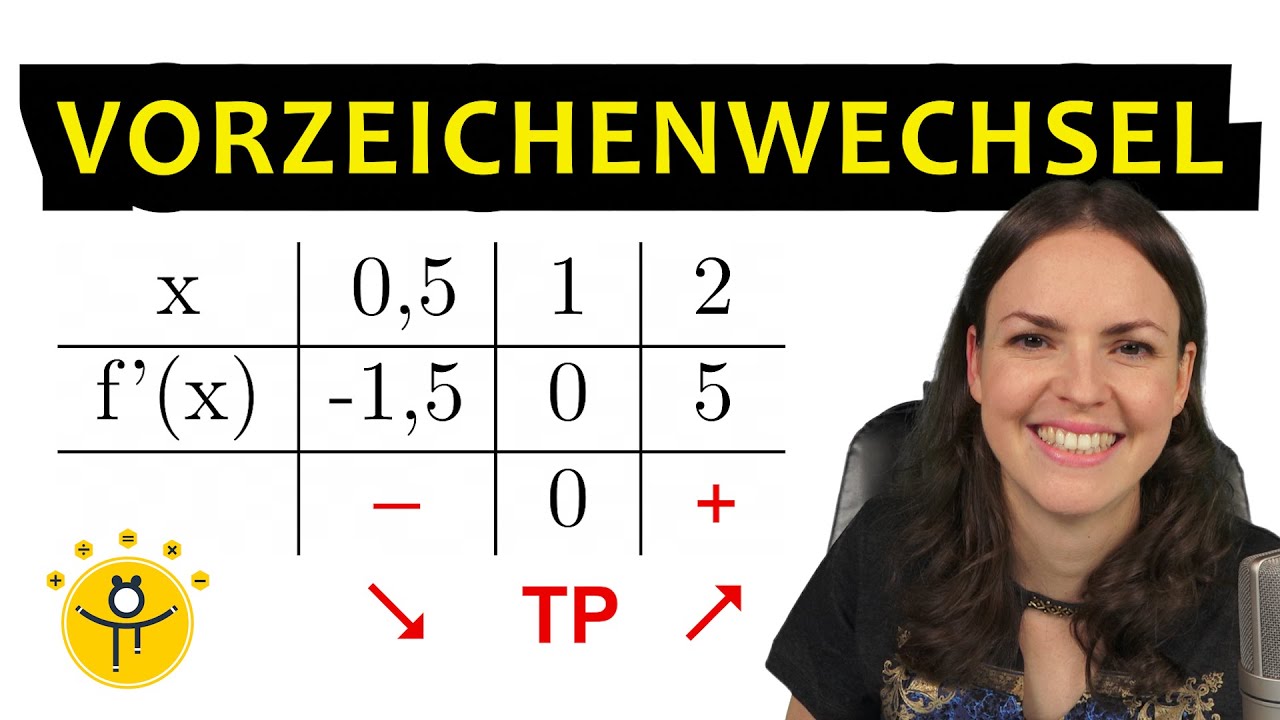
EXTREMA Vorzeichenwechsel Kriterium – Hochpunkt Tiefpunkt berechnen

MONOTONIE berechnen Ableitung – Monotonieverhalten Mathe, Intervall

Erörterung schreiben I musstewissen Deutsch

So beweist du dem Finanzamt deine Auswanderung – diese Belege zählen wirklich
5.0 / 5 (0 votes)
