Notwendige und Hinreichende Bedingung ?häää!!! Kurvendiskussion Übersicht - simplexy.de
Summary
TLDRIn diesem Video lernen wir, wie man Extremstellen einer Funktion findet. Zunächst wird erklärt, dass extremen Punkte dort auftreten, wo die erste Ableitung der Funktion null ist. Dies ist die notwendige Bedingung, um potenzielle Extremstellen zu identifizieren. Doch um sicherzustellen, dass es sich wirklich um ein Minimum oder Maximum handelt, muss die zweite Ableitung überprüft werden. Ist die zweite Ableitung positiv, handelt es sich um ein Minimum, bei negativem Wert um ein Maximum. Falls die zweite Ableitung null ergibt, könnte es sich um einen Sattel- oder Wendepunkt handeln. Beide Bedingungen müssen erfüllt sein, damit eine Funktion echte Extremstellen besitzt.
Takeaways
- 😀 Die extremen Punkte einer Funktion werden durch die Ableitung bestimmt.
- 😀 Um die extremen Punkte zu finden, setzt man die erste Ableitung gleich null.
- 😀 Eine Funktion hat nur dann extremen Punkte, wenn die erste Ableitung an einer Stelle null ist.
- 😀 Ein Sattelpunkt ist ein Punkt, an dem die erste Ableitung null ist, aber kein Extrempunkt vorliegt.
- 😀 Die erste Ableitung gibt nur an, wo potenzielle extreme Stellen existieren, aber nicht, ob sie tatsächlich Extrempunkte sind.
- 😀 Die zweite Ableitung hilft dabei, festzustellen, ob eine potenzielle Extremstelle tatsächlich ein Extrempunkt ist.
- 😀 Eine positive zweite Ableitung an einer extremen Stelle bedeutet, dass es sich um einen Tiefpunkt handelt.
- 😀 Eine negative zweite Ableitung an einer extremen Stelle bedeutet, dass es sich um einen Hochpunkt handelt.
- 😀 Wenn die zweite Ableitung null ist, handelt es sich wahrscheinlich um einen Wendepunkt oder Sattelpunkt, nicht um einen Extrempunkt.
- 😀 Eine Funktion besitzt nur dann extremen Punkte, wenn sowohl die notwendige als auch die hinreichende Bedingung erfüllt sind.
Q & A
Was ist der erste Schritt, um Extremstellen einer Funktion zu finden?
-Der erste Schritt ist, die erste Ableitung der Funktion zu berechnen und diese gleich null zu setzen. Dadurch findet man die potenziellen Extremstellen.
Warum ist die Bedingung f'(x) = 0 notwendig für Extremstellen?
-Die Bedingung f'(x) = 0 ist notwendig, weil Extremstellen dort liegen, wo die Steigung der Funktion null ist. Aber das allein reicht nicht aus, um zu bestätigen, dass es sich um einen Extrempunkt handelt.
Was bedeutet es, wenn die zweite Ableitung an einer potenziellen Extremstelle null ergibt?
-Wenn die zweite Ableitung an einer potenziellen Extremstelle null ergibt, dann ist die zweite Ableitungstest nicht aussagekräftig. In diesem Fall könnte es sich um einen Wendepunkt oder einen Sattelpunkt handeln, aber nicht um einen Extrempunkt.
Wie kann man erkennen, ob es sich an einer potenziellen Extremstelle um einen Hoch- oder Tiefpunkt handelt?
-Um zu bestimmen, ob es sich um einen Hoch- oder Tiefpunkt handelt, schaut man sich die zweite Ableitung an. Wenn f''(x) > 0, liegt ein Tiefpunkt vor, und wenn f''(x) < 0, handelt es sich um einen Hochpunkt.
Was passiert, wenn f'(x) an einer Stelle gleich null ist, aber f''(x) kleiner als null?
-Wenn f'(x) = 0 und f''(x) < 0, dann handelt es sich an dieser Stelle um einen Hochpunkt der Funktion.
Was ist der Unterschied zwischen einer notwendigen und einer hinreichenden Bedingung in Bezug auf Extremstellen?
-Die notwendige Bedingung ist, dass f'(x) = 0 für potenzielle Extremstellen, aber dies garantiert nicht, dass es sich um Extremstellen handelt. Die hinreichende Bedingung ist die zweite Ableitung f''(x), die bestätigt, ob an einer potenziellen Extremstelle tatsächlich ein Extrempunkt vorliegt.
Warum kann eine Funktion trotz f'(x) = 0 an einer Stelle keinen Extrempunkt haben?
-Eine Funktion kann an einer Stelle mit f'(x) = 0 keinen Extrempunkt haben, wenn die zweite Ableitung an dieser Stelle null ist. In diesem Fall handelt es sich wahrscheinlich um einen Wendepunkt oder Sattelpunkt.
Was passiert, wenn die zweite Ableitung an einer potenziellen Extremstelle größer als null ist?
-Wenn die zweite Ableitung an einer potenziellen Extremstelle größer als null ist, liegt dort ein Tiefpunkt der Funktion vor.
Was bedeutet es, wenn f''(x) kleiner als null ist?
-Wenn f''(x) an einer potenziellen Extremstelle kleiner als null ist, handelt es sich um einen Hochpunkt, da die Funktion dort nach unten gekrümmt ist.
Was sollte man tun, wenn f'(x) = 0 an einer Stelle und die zweite Ableitung ebenfalls null ergibt?
-Wenn f'(x) = 0 und f''(x) = 0 an einer Stelle, dann muss man weiter untersuchen, ob es sich um einen Wendepunkt oder einen Sattelpunkt handelt. Eine genauere Analyse ist erforderlich, da der zweite Ableitungstest nicht aussagekräftig ist.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

MONOTONIE berechnen Ableitung – Monotonieverhalten Mathe, Intervall

Bestimmung von Tangenten - Die Tangentengleichung | Differenzialrechnung | Flip the Classroom
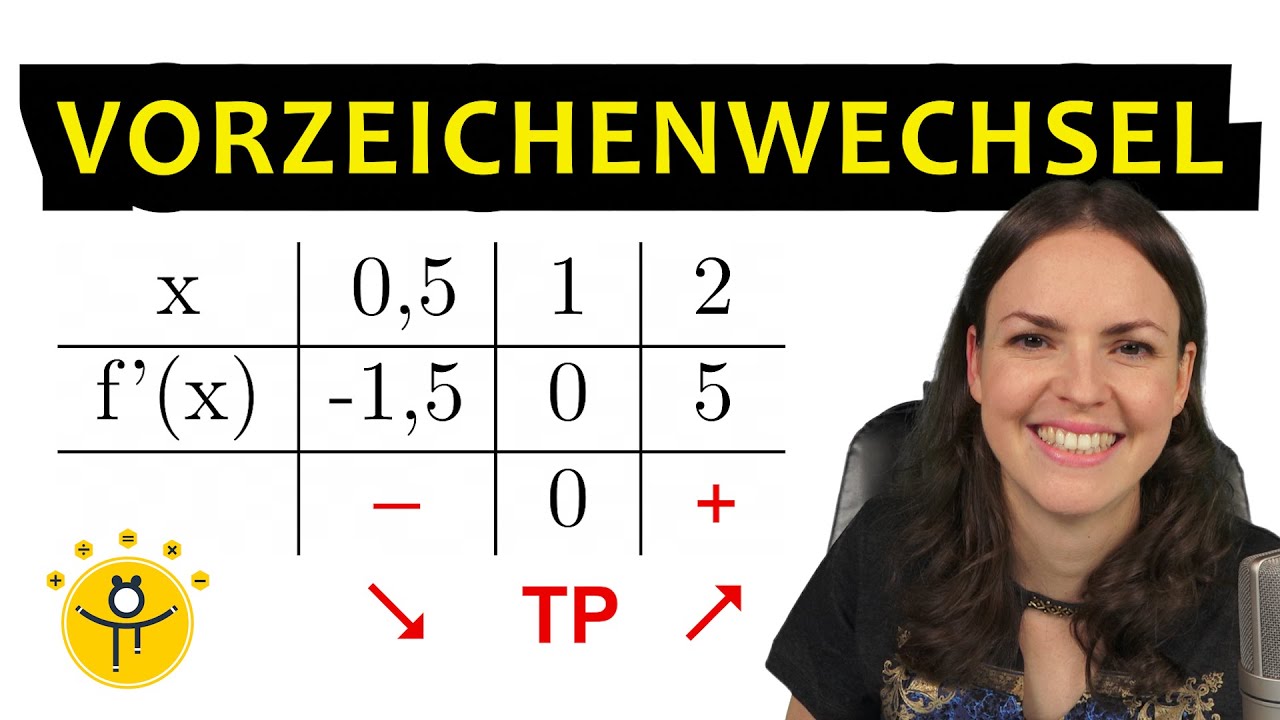
EXTREMA Vorzeichenwechsel Kriterium – Hochpunkt Tiefpunkt berechnen

Graphisches Ableiten - Graph der Ableitung skizzieren | Differenzialrechnung | Flip the Classroom

NULLSTELLEN durch Ausklammern und pq Formel bestimmen – Nullstellen berechnen Ausklammern

Built-in functions, constructors, and callables
5.0 / 5 (0 votes)
