EXTREMA Vorzeichenwechsel Kriterium – Hochpunkt Tiefpunkt berechnen
Summary
TLDRIn diesem Video wird erklärt, wie man Hoch- und Tiefpunkte einer Funktion mit dem Vorzeichenwechselkriterium berechnet. Der Prozess umfasst das Bilden der ersten Ableitung, das Setzen der Ableitung gleich Null, um kritische Punkte zu finden, und das Anwenden des Vorzeichenwechselkriteriums, um zu bestimmen, ob diese Punkte Hochpunkte oder Tiefpunkte sind. Es wird gezeigt, wie man anhand der Steigung vor und nach den kritischen Punkten untersucht, ob die Funktion steigt oder fällt. Abschließend werden die y-Koordinaten der Extremstellen berechnet, um die vollständigen Extrempunkte zu bestimmen.
Takeaways
- 😀 Die erste Ableitung einer Funktion gibt die Steigung an und hilft dabei, Extremstellen (Hochpunkte, Tiefpunkte, Sattelpunkte) zu finden.
- 😀 Ein Hochpunkt ist eine Stelle, an der die Steigung von positiv zu negativ wechselt, während ein Tiefpunkt von negativ zu positiv wechselt.
- 😀 Die Berechnung der ersten Ableitung ist der erste Schritt, um Extremstellen zu bestimmen. Die Ableitung muss null gesetzt werden, um kritische Punkte zu finden.
- 😀 Bei der Lösung der ersten Ableitung durch Ausklammern kann man schnell die kritischen Punkte finden, indem man den Nullprodukt-Satz anwendet.
- 😀 Für jedes kritische Punkt x = 0 und x = 1 wird überprüft, ob es sich um einen Hochpunkt oder Tiefpunkt handelt, basierend auf der Steigungsänderung.
- 😀 Das Vorzeichenwechselkriterium untersucht, ob die Steigung vor und nach einem kritischen Punkt positiv oder negativ ist, um Hoch- oder Tiefpunkte zu klassifizieren.
- 😀 Ein Vorzeichenwechsel von positiv zu negativ deutet auf einen Hochpunkt hin, während ein Wechsel von negativ zu positiv auf einen Tiefpunkt hindeutet.
- 😀 Teststellen werden links und rechts von den kritischen Punkten gewählt, um die Steigung und das Vorzeichen zu prüfen und den Punkt als Hoch- oder Tiefpunkt zu bestätigen.
- 😀 Das Vorzeichenwechselkriterium hilft nicht nur bei der Bestimmung von Extrempunkten, sondern auch bei der Entdeckung von Sattelpunkten, wenn das Vorzeichen nicht wechselt.
- 😀 Nach der Bestimmung der x-Koordinaten der Extremstellen werden die entsprechenden y-Koordinaten durch Einsetzen in die ursprüngliche Funktion berechnet.
Q & A
Was ist der erste Schritt, um Hoch- und Tiefpunkte einer Funktion zu berechnen?
-Der erste Schritt besteht darin, die erste Ableitung der Funktion zu bilden, da diese die Steigung der Funktion angibt. Die Steigung ist entscheidend, um Extremstellen wie Hoch- oder Tiefpunkte zu finden.
Warum setzen wir die erste Ableitung gleich Null?
-Die erste Ableitung wird gleich Null gesetzt, weil an den Stellen, an denen die Steigung Null ist, potenziell Extremstellen wie Hoch- oder Tiefpunkte oder Sattelpunkte liegen.
Welche Rolle spielt die Hochzahl in der Differentiation?
-Die Hochzahl ist entscheidend, weil sie bei der Ableitung mit der Zahl vor der Variablen multipliziert wird und danach um eins verringert wird, um die neue Potenz zu bestimmen.
Wie lösen wir die Gleichung der ersten Ableitung nach Null auf?
-Wir setzen die erste Ableitung gleich Null und lösen die resultierende Gleichung durch Ausklammern oder, falls nötig, mit der pq-Formel. Das ergibt die x-Werte der kritischen Stellen.
Was ist der Unterschied zwischen einem Hochpunkt und einem Tiefpunkt?
-Ein Hochpunkt tritt auf, wenn die Steigung der Funktion von positiv (bergauf) zu negativ (berab) wechselt. Ein Tiefpunkt tritt auf, wenn die Steigung von negativ (bergab) zu positiv (bergauf) wechselt.
Was ist das Vorzeichenwechselkriterium und wie wird es angewendet?
-Das Vorzeichenwechselkriterium untersucht die Steigung der Funktion vor und nach einer kritischen Stelle. Wenn die Steigung von positiv auf negativ wechselt, handelt es sich um einen Hochpunkt. Wenn sie von negativ auf positiv wechselt, handelt es sich um einen Tiefpunkt.
Was passiert, wenn die Steigung an einer kritischen Stelle nicht wechselt?
-Wenn die Steigung an einer kritischen Stelle nicht wechselt, handelt es sich um einen Sattelpunkt, da keine extremen Werte (Hoch- oder Tiefpunkt) vorhanden sind.
Wie wählen wir die Teststellen für das Vorzeichenwechselkriterium aus?
-Teststellen werden direkt links und rechts der kritischen Stellen gewählt, um die Steigung in diesen Bereichen zu überprüfen. Diese Punkte sollten möglichst nah an den kritischen Stellen liegen, aber nicht direkt auf ihnen.
Wie berechnen wir die y-Koordinaten der Extremstellen?
-Nachdem die x-Koordinaten der Extremstellen (Hoch- und Tiefpunkte) gefunden wurden, setzen wir diese in die ursprüngliche Funktion ein, um die entsprechenden y-Koordinaten zu berechnen.
Was ist der letzte Schritt, nachdem der Vorzeichenwechsel durchgeführt wurde?
-Der letzte Schritt besteht darin, die y-Koordinaten der gefundenen Extremstellen zu berechnen, indem die entsprechenden x-Werte in die ursprüngliche Funktion eingesetzt werden.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

MONOTONIE berechnen Ableitung – Monotonieverhalten Mathe, Intervall
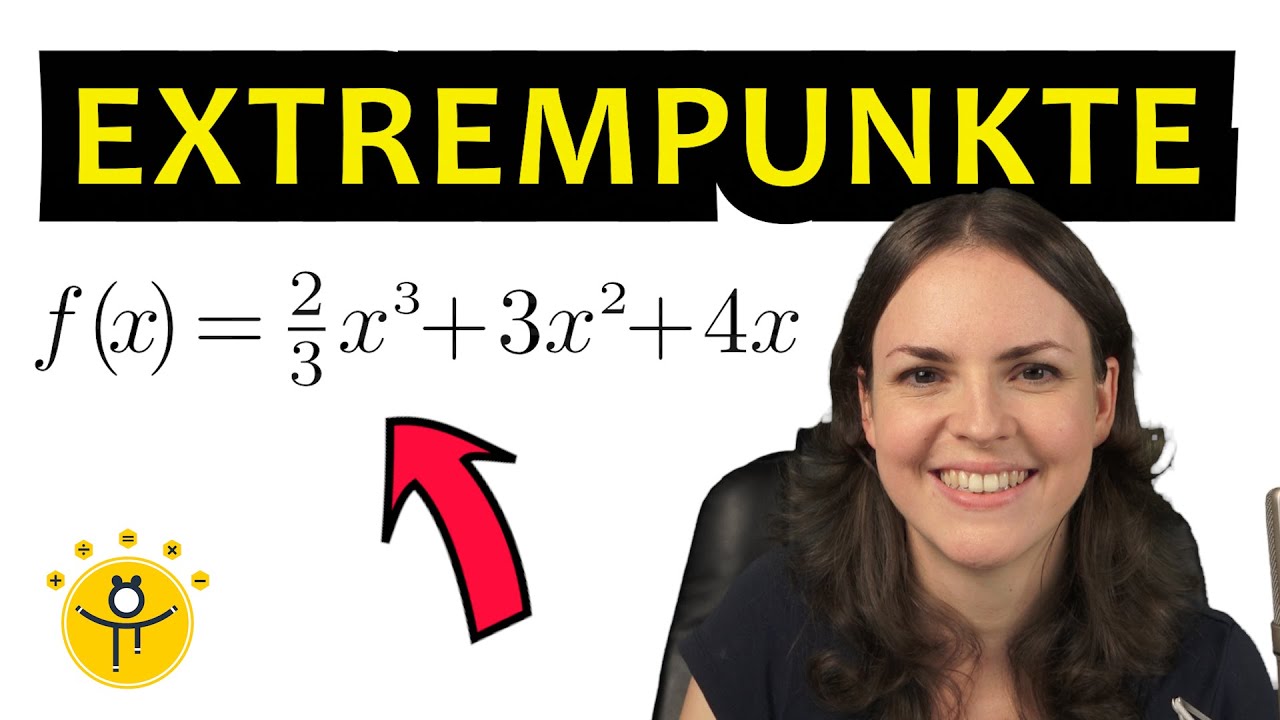
EXTREMPUNKTE berechnen für Anfänger – Ableitung ganzrationaler Funktionen bestimmen
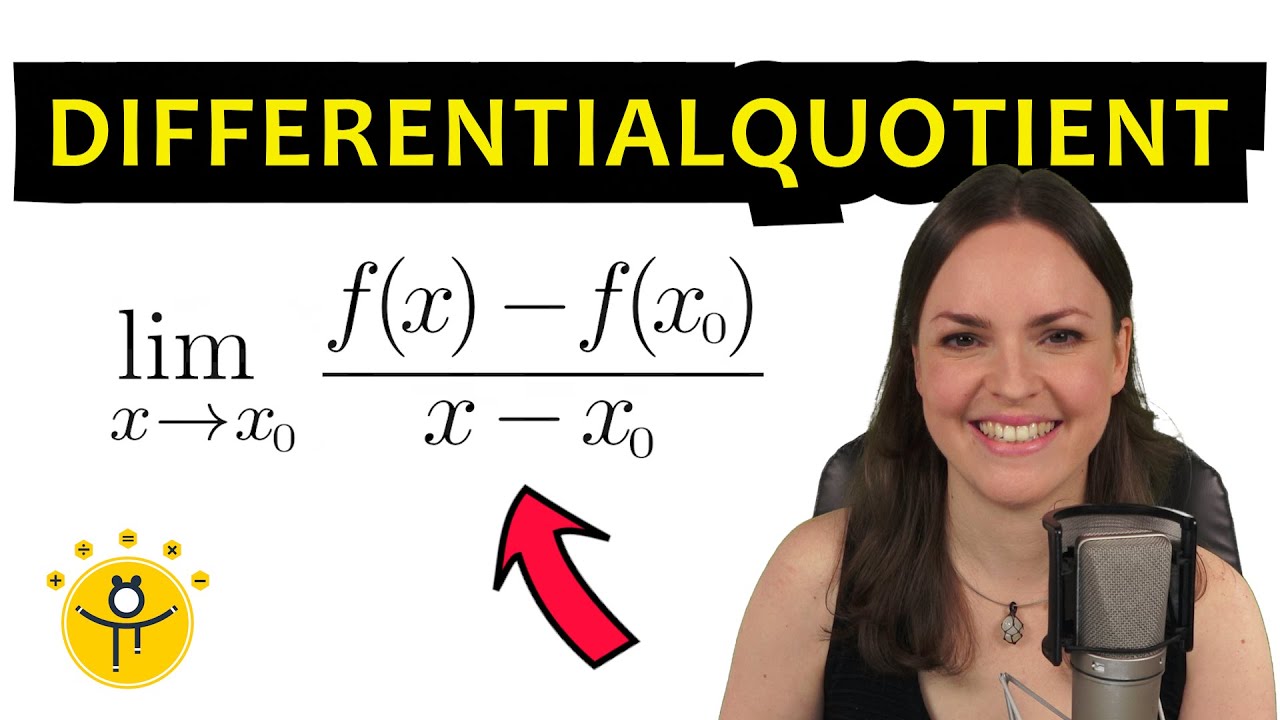
Differentialquotient berechnen – Limes, Ableitung Beispiel

Ableitung Grundlagen

Bestimmung von Tangenten - Die Tangentengleichung | Differenzialrechnung | Flip the Classroom

ALLE Nullstellen berechnen – Ganzrationale Funktionen, Polynom
5.0 / 5 (0 votes)
