Menghitung panjang tali busur lingkaran
Summary
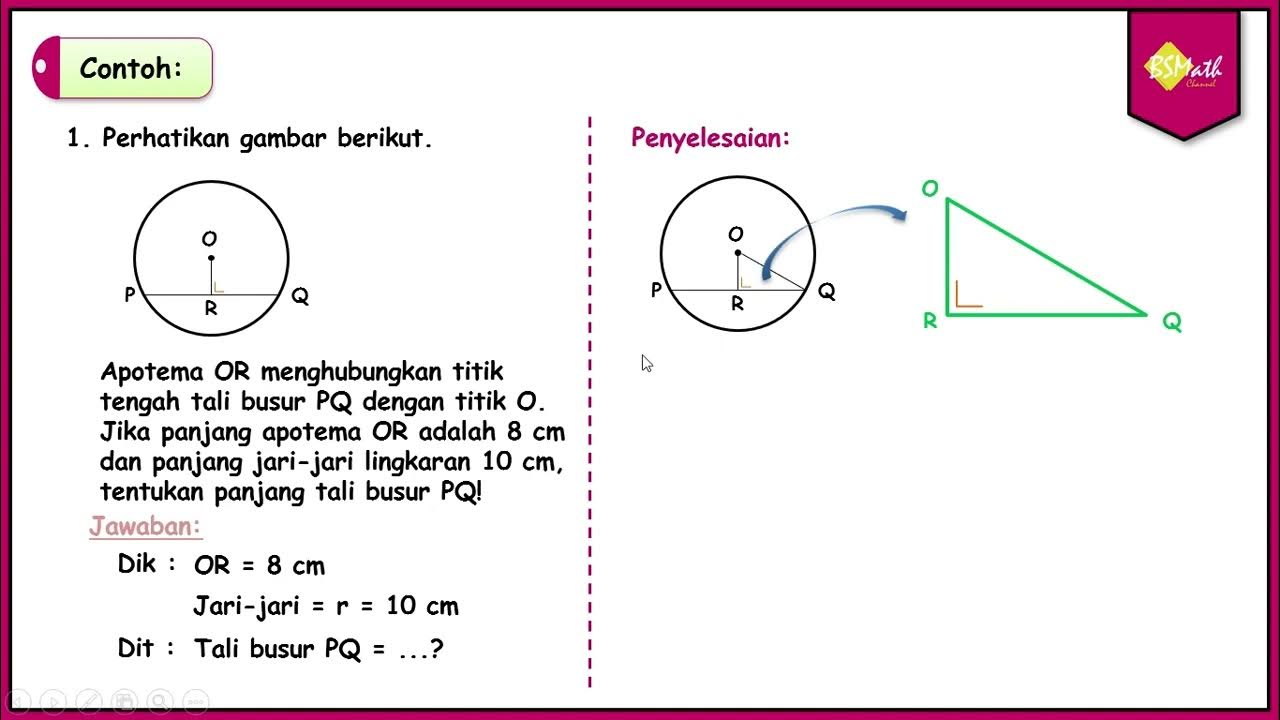
TLDRThe video explains how to calculate the length of the chord in a circle using the Pythagorean theorem. Given the radius of the circle as 15 cm and the apothem (distance from the center to the chord) as 9 cm, the speaker demonstrates how to find the length of the chord. By applying the Pythagorean theorem, the length of the segment QR is calculated as 12 cm. Since QR equals PR, the total length of the chord PQ is twice this value, resulting in 24 cm.
Takeaways
- 📏 The radius of the circle is 15 cm.
- 📐 The length of the apothem (OR) is 9 cm.
- 🎯 The goal is to find the length of the chord PQ.
- 🔗 OR is perpendicular to PQ.
- 🧮 To calculate the length of QR, the Pythagorean theorem is used.
- ✔️ The hypotenuse is the radius, and one leg is the apothem.
- ➖ Apply the Pythagorean theorem: 15^2 - 9^2.
- ➗ 15^2 equals 225, and 9^2 equals 81.
- 📊 Subtract 81 from 225 to get 144.
- 🔢 The square root of 144 is 12 cm, so QR and PR are both 12 cm, making PQ 24 cm.
Q & A
What is the radius of the circle mentioned in the script?
-The radius of the circle is 15 cm.
What is the length of the apothem (OR) in the problem?
-The length of the apothem OR is 9 cm.
How is the length of the chord PQ calculated?
-The length of the chord PQ is calculated using the Pythagorean theorem, as the apothem OR is perpendicular to PQ, forming a right triangle.
What is the formula used to calculate the length of QR?
-The Pythagorean theorem is used: \( QR = \sqrt{r^2 - apothem^2} \), where \( r = 15 \text{cm} \) and \( apothem = 9 \text{cm} \).
What is the square of the radius of the circle?
-The square of the radius is \( 15^2 = 225 \text{cm}^2 \).
What is the square of the apothem OR?
-The square of the apothem OR is \( 9^2 = 81 \text{cm}^2 \).
How is QR calculated after applying the Pythagorean theorem?
-QR is calculated as \( \sqrt{225 - 81} = \sqrt{144} = 12 \text{cm} \).
Why is QR equal to PR in the problem?
-QR is equal to PR because the apothem bisects the chord PQ, making the two halves (QR and PR) equal.
What is the total length of the chord PQ?
-The total length of the chord PQ is \( 2 \times 12 \text{cm} = 24 \text{cm} \).
What mathematical concept is primarily used to solve this problem?
-The Pythagorean theorem is primarily used to solve the problem.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Soal Layang-Layang Garis Singgung | Garis Singgung Lingkaran 11 SMA KMerdeka
Tali Busur Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka
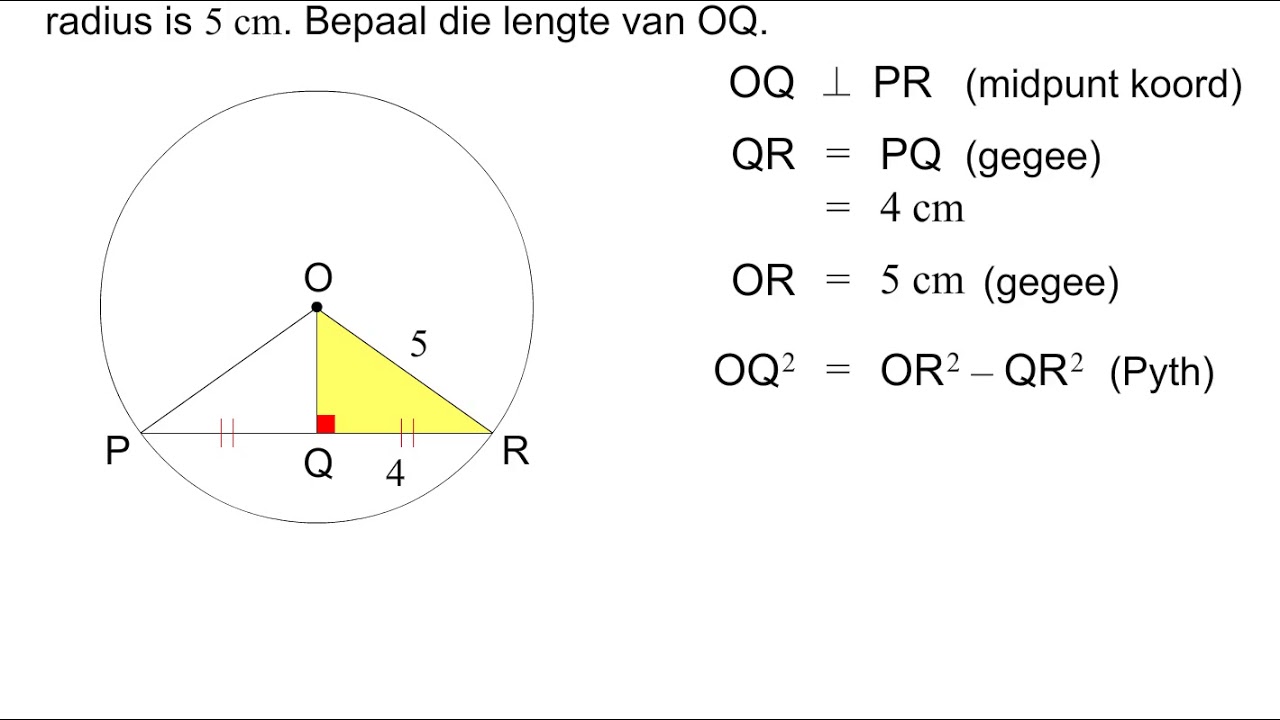
Graad 11 Meetkunde
The Pythagorean Theorem: Extensions and Applications

Lingkaran kelas 11 / Video Teorema Lingkaran

COMO HALLAR O CALCULAR LA GENERATRIZ DE UN CONO TRUNCADO
5.0 / 5 (0 votes)
