The Pythagorean Theorem: Extensions and Applications

Summary

This video explores various applications of the Pythagorean theorem, starting with finding the distance between points on an XY grid, such as those used in computer graphics. It explains how to calculate this distance using the difference in coordinates and introduces the concept of delta (Δ) for differences. The video then extends the theorem to three dimensions, illustrating how to find distances across 3D objects using a similar approach. Finally, it demonstrates how to derive the equation of a circle on a plane, showing practical uses of the Pythagorean theorem in algebra and geometry.

Takeaways

• 📏 The video discusses extensions and applications of the Pythagorean theorem, focusing on finding distances between points on a graph.
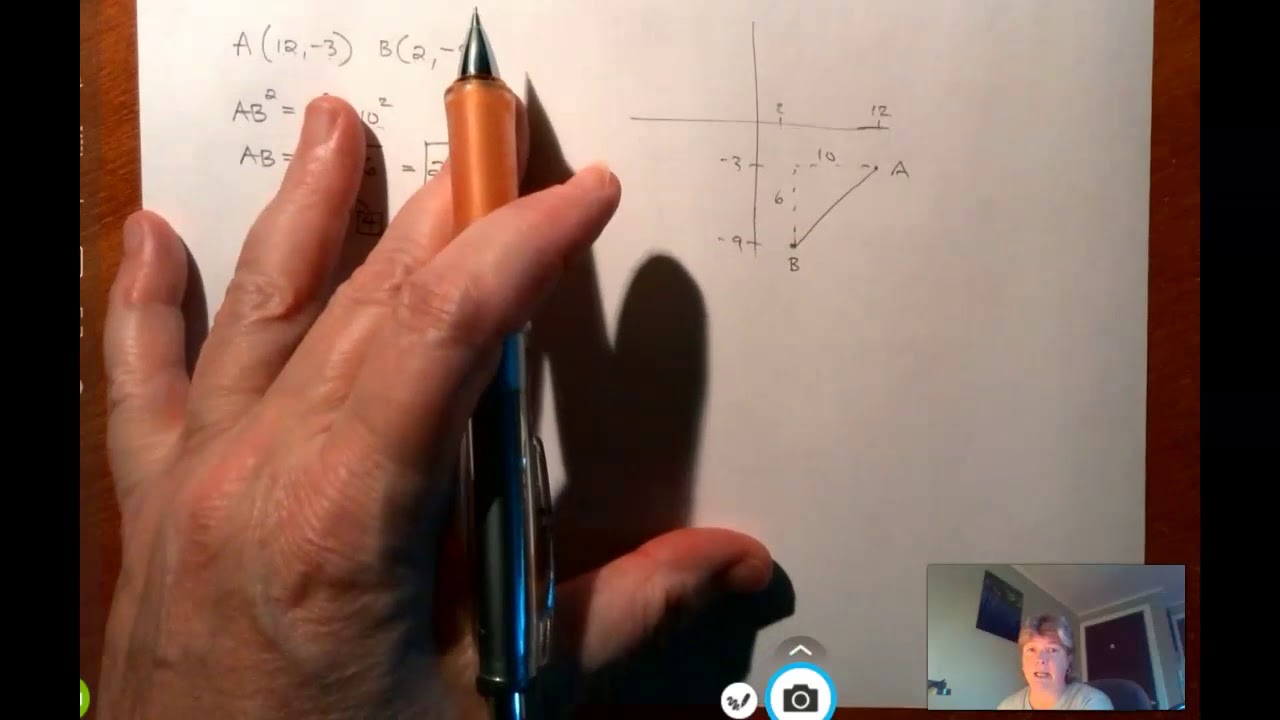
• 📉 The distance formula can be applied to find the distance between two points on an XY grid by creating a right triangle and using the Pythagorean theorem.
• 🔢 To find the horizontal and vertical distances between points, subtract the respective X and Y coordinates and use these differences in the distance formula.
• 🔄 The formula for the distance between two points on a plane is derived by squaring the differences in X and Y values, adding them, and taking the square root.
• 🌐 The video extends the concept to three dimensions, explaining how to find the diagonal distance across a three-dimensional object using a similar approach.
• 🏠 In three dimensions, the distance formula incorporates the length, width, and height of the object, leading to a generalized Pythagorean theorem for 3D space.
• 🔍 The process of finding the diagonal in 3D involves first finding the distance across the floor (a 2D problem) and then using this distance in a new right triangle that includes the height.
• 📐 The video also explains how to find the equation of a circle on a plane, using the Pythagorean theorem to relate the radius and the coordinates of points on the circle.
• 🔵 The equation of a circle is derived from the relationship between the radius and the coordinates of any point on the circle, written as x^2 + y^2 = r^2.
• 🎨 Applications in graphics and geometry software are highlighted, showing how programs like GeoGebra use these equations to plot circles and other shapes on a coordinate plane.

Q & A

What is the primary application of the Pythagorean theorem discussed in the video?

The primary application discussed is finding the distance between two points on an XY grid using the Pythagorean theorem.

How is the distance between two points on a graph calculated?

The distance is calculated by finding the horizontal and vertical distances between the points, squaring them, adding the squares, and then taking the square root of the sum.

What are Delta X and Delta Y in the context of the distance formula?

Delta X represents the difference in the X coordinates of the two points, and Delta Y represents the difference in the Y coordinates.

How does the video extend the Pythagorean theorem to three dimensions?

The video extends the Pythagorean theorem to three dimensions by demonstrating how to calculate the diagonal distance across a three-dimensional object using the lengths, widths, and heights of the sides.

How is the diagonal distance across a three-dimensional space calculated?

The diagonal distance is calculated by taking the square root of the sum of the squares of the length, width, and height.

What is the equation for a circle derived in the video?

The equation for a circle is \( x^2 + y^2 = r^2 \), where r is the radius of the circle.

How is the concept of a right triangle used to find the equation of a circle?

The concept is used by noting that the radius forms the hypotenuse of a right triangle, with the legs being the X and Y coordinates, thus leading to the equation \( r^2 = x^2 + y^2 \).

What is the significance of using coordinate numbers in calculating distances on a graph?

Using coordinate numbers allows for precise distance calculations, which is crucial when dealing with non-integer or decimal coordinates where simply counting squares is not feasible.

How does the video suggest visualizing three-dimensional space for applying the extended Pythagorean theorem?

The video suggests visualizing the room you're in as a box-like structure and imagining the diagonal distance between a top corner and an opposite bottom corner.

What practical applications of the distance formula are mentioned in the video?

Practical applications mentioned include plotting graphics on a computer screen, determining distances in various fields like graphic design, and defining geometrical shapes like circles.

Outlines

00:00

📏 Applying the Pythagorean Theorem to Graph Distances

This paragraph introduces the use of the Pythagorean theorem to find distances between points on a two-dimensional graph, such as an XY grid found on television or computer screens. It explains the concept by visualizing the distance as the hypotenuse of a right triangle formed by the horizontal and vertical distances between two points. The process involves identifying the points by their coordinates, calculating the differences in the x (horizontal) and y (vertical) values, squaring these differences, summing them, and then taking the square root of the result to find the distance. The paragraph also introduces the notation Δx for the difference in x-coordinates and Δy for the difference in y-coordinates, emphasizing the general applicability of this method even when dealing with decimal numbers.

05:01

📐 Extending the Pythagorean Theorem to Three Dimensions

The second paragraph extends the concept of the Pythagorean theorem from two to three dimensions, illustrating how to find the distance across space within a room, from one corner where a wall meets the ceiling to the opposite corner on the floor. It likens this to finding the diagonal of a rectangle but in three dimensions, involving the length (L), width (W), and height (H) of the room. The process involves first calculating the distance across the floor (X) using the Pythagorean theorem for a two-dimensional rectangle (L^2 + W^2), and then using this result as one leg of a new right triangle to find the total diagonal distance (D) using the formula D = √(X^2 + H^2). This paragraph also provides an example calculation for a room with given dimensions, demonstrating the practical application of this three-dimensional extension of the Pythagorean theorem.

10:02

📘 Finding the Equation of a Circle Using Distance

The third paragraph discusses the application of distance concepts to derive the equation of a circle. It explains that any point on a circle is at a constant distance (the radius, R) from the center of the circle. By considering a right triangle formed by the radius and the x and y coordinates of a point on the circle, the relationship R^2 = x^2 + y^2 is established, which is the equation of the circle. The paragraph also demonstrates the use of GeoGebra software to visualize and manipulate the equation of a circle, showing how changing the radius value alters the size of the circle on the graph, and how the algebraic equation directly corresponds to the geometric representation.

15:03

🎨 Practical Applications of Distance Formulas in Graphics

The final paragraph ties together the concepts discussed in the previous sections, emphasizing their practical applications in various fields, particularly in graphic design and computer graphics. It highlights that understanding the mathematical principles behind these applications allows for better use of graphic manipulation tools and can be valuable for professionals in the field. The paragraph concludes by noting the importance of the Pythagorean theorem and its extensions in defining not only straight lines but also curves, such as circles, on graphs.

Keywords

💡Pythagorean Theorem

The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem is central to the video's theme as it explains how to find distances on a graph, and how this principle can be extended to three-dimensional spaces. For example, in the video, it is used to find the distance between two points on an XY grid.

💡Distance Formula

The distance formula is derived from the Pythagorean Theorem and is used to calculate the distance between two points in a plane. The formula is sqrt((x2 - x1)^2 + (y2 - y1)^2). In the video, this formula is applied to find the distance between points on a graph, emphasizing its practical applications in plotting graphics on screens.

💡Coordinates

Coordinates are a set of values that show an exact position on a graph or grid, typically defined as (x, y). In the video, the coordinates (2, 3) and (7, 5) are used to demonstrate how to calculate distances using the distance formula, highlighting the importance of understanding how to read and use coordinate systems.

💡Right Triangle

A right triangle is a triangle in which one angle is a right angle (90 degrees). The Pythagorean Theorem applies to right triangles, and the video uses this concept to explain how to calculate distances on a graph. By forming a right triangle with the coordinates, the hypotenuse represents the distance between the points.

💡Delta (Δ)

Delta (Δ) represents the difference between two values. In the video, Δx and Δy are used to denote the differences in the x and y coordinates of two points, respectively. These differences are squared and summed to apply the distance formula.

💡Square Root

The square root is a value that, when multiplied by itself, gives the original number. In the distance formula, the square root is used to determine the actual distance after summing the squares of the coordinate differences. The video demonstrates using a calculator to find the square root of 29 to get the final distance.

💡Hypotenuse

The hypotenuse is the longest side of a right triangle, opposite the right angle. In the video, finding the hypotenuse of the right triangle formed by two points on a graph is essential for calculating the distance between those points using the Pythagorean Theorem.

💡Three-Dimensional Extension

This refers to extending the Pythagorean Theorem to three dimensions to find the diagonal distance in a 3D space. The video explains how to calculate the diagonal distance across a room by considering the lengths, widths, and heights, ultimately summing their squares and taking the square root.

💡Equation of a Circle

The equation of a circle in a coordinate plane is x^2 + y^2 = r^2, where r is the radius. The video introduces this concept by demonstrating how to find the equation of a circle given a specific radius, using the distance from the center to any point on the circle.

💡Graph Plotting

Graph plotting involves placing points on a coordinate grid to represent data or mathematical functions. The video discusses the practical applications of graph plotting, such as in computer graphics, and how understanding distances and coordinates is crucial for accurately plotting graphs.

Highlights

The video discusses extensions and applications of the Pythagorean theorem.

It explains how to find the distance between points on an XY grid, like on a television or computer screen.

The distance formula is derived by creating a right triangle with horizontal and vertical distances as legs.

The horizontal and vertical distances between points are calculated using coordinate differences.

The distance formula is represented as the square root of the sum of the squares of the differences in X and Y coordinates.

The concept of Delta X and Delta Y is introduced to represent the differences in X and Y coordinates.

A practical application of the distance formula is demonstrated with an example using counting squares on a graph.

Decimal coordinates are also considered for calculating distances, emphasizing the formula's utility beyond whole numbers.

The video extends the Pythagorean theorem to three dimensions, showing how to find the diagonal of a room.

A two-step process is introduced to calculate distances in three-dimensional space, involving the diagonal of a rectangle on the floor.

The three-dimensional distance formula is presented as the square root of the sum of the squares of length, width, and height.

An example calculation is shown to find the diagonal of a three-dimensional object using the extended Pythagorean theorem.

The video demonstrates finding the equation of a circle using the Pythagorean theorem, with the circle's radius as the hypotenuse.

Geogebra is used to visually represent the equation of a circle and its relationship to the Pythagorean theorem.

The equation x^2 + y^2 = R^2 is shown to describe any circle, where R is the radius.

The video highlights the importance of understanding algebraic concepts for practical applications in graphic design and art.

The video concludes by emphasizing the versatility of the Pythagorean theorem in various mathematical and real-world contexts.

Transcripts

okay this video is going to deal with

several extensions and applications of

the Pythagorean

theorem and one that I'd like to start

off with is how to find distance between

points on a graph on XY grid like this

one place by the way where XY grids

occur is on a television screen or a

computer screen

and you're trying to um uh plot graphics

and so forth if you have a program that

plots the graphs it identifies the

points by numbers how far over and how

far up from some coordinate system like

this and one of the things you might

want to know is how far is it between

two

points um there's a lot of applications

of this but let's just see in general

how would we find that

distance well first let's draw that

distance in and if you look at it a

little bit it looks like we have a

triangle

here if I go along the coordinate grid

looks like we have a horizontal and a

vertical line connecting this to make a

right triangle and the distance we're

looking for is the hypotenuse so if we

could find the horizontal distance

between these points and the vertical

distance between these points we could

take those numbers square them add them

together and take the square root and we

got the distance okay

well first let's identify the points by

their numbers notice this one is over

two and up three so I write two

three this one is over 1 2 3 4 5 6 7 and

up 1 2 3 4 five so this is

7 five all

right now we could just look at the

graph and say oh from here we have to

step over here 1 2 3 4 5 squares and up

two but uh what if these were decimal

numbers and so forth sometimes we don't

want to Simply count squares on a graph

we want to compute the distance based on

these coordinate numbers themselves and

so let's see what these numbers

mean first of all notice that this first

number the two is how far over

horizontally this point is so to get to

this point we go over two and up

three this point this number seven is

how

far horizontally we have to go to get to

this distance over here and so if I want

to find the horizontal distance between

the points it's like taking 7 minus 2

and that gives me

five okay so I take the difference so I

take 7 - 2 and that's it's going to give

me the horizontal distance notice the

same thing applies vertically the three

here is how far up I have to go uh from

the x- axis to get up to this

level and five is how far I have to go

up from the x-axis to get to this level

and so how far different are they how

far apart are they

vertically well I Take 5 - 3 and that

gives us 2 2 so I take the 7 - 2 and

then I take my 5 -

3 if I Square each of these and add them

together and take the square root that's

going to give me the distance between

the

points okay so the way we write this

there's a abbreviation we sometimes use

the difference in the X values we

sometimes write as simply Delta X that's

the Greek letter for Delta

and it has a D sound in Greek and so it

stands for the difference of the X

values this x value is 7 this one is two

so Delta X or the difference of the X's

is five take Delta X and square it then

I take Delta y this y value is five this

one is three the difference of the Y

values is 2 so I take my Delta Y and

square it add them together and take the

square root and this is the distance

formula for a two-dimensional

surface okay let's just go ahead and

finish it out if I do it from the

numbers or if I do it from Counting

squares either one 7 - 2 is 5 is

25 5 - 3 is 2^ 2ar is 4 add them

together I get 29 and so the distance

between the points is a square < TK of

29 at this stage we're just going to use

a

calculator okay and so if I just take 29

and hit the square root by the way for

the rest of this um the

exercises um in this uh unit uh we'll go

ahead and use a calculator um unless

we're specifically practicing the square

root technique from the last video okay

and so there you go four uh

5.38 or you might round it up to 5.39

okay that's the distance formula in two

Dimensions let's see how we can

generalize what we know about the

Pythagorean theorem to finding a

distance across space so a diagonal uh

across a three-dimensional object look

at look around yourself at the room

you're sitting in assuming you're in a

standard sort of box-like room and

imagine

wanting to know the distance from the

top corner where one of the walls meets

the ceiling and the bottom corner here

where the opposite wall or the opposite

uh vertical line like this meets the

floor and we want to take uh let's use a

different color here we want to find

this

distance okay so if you look around

physically in the room you're sitting in

and try to um imagine in your

circumstance what I'm trying to draw

here that'll make it more real to you so

if I have a two-dimensional situation I

could find the diagonal of a rectangle

and uh by finding um the hypotenuse of a

right triangle notice that if I split a

rectangle like this I have a right

triangle whose legs are simply L and W

the length and the width of the

rectangle okay so in this case the

distance

here is simply the square root of the

sum of the squares of the two legs l^2 +

w^2 if I had numbers I would Square them

add them together and take the square

root as we've been doing

before now what do we do for a

three-dimensional

situation well we have to build somehow

on what we already know we can't just

jump to conclusions here okay so let's

go back and see is this distance we're

looking for part of a right triangle

whose uh legs we can find all right and

notice that if I go this length along

think of that as a hypotenuse of a

triangle and think of the the height

along this edge here as one leg then the

distance across the floor would be the

other leg so look at this red triangle

here that's uh simply a right triangle

and that has two legs if I could find

both legs this one I know is H if I can

find this length I can then uh put them

together and find uh this distance D

that I'm looking for

here okay well we're going to have to

somehow figure out this distance across

the floor and if you look at it isn't

that a lot like finding the distance

across a rectangle because the floor

itself looks like a rectangle laid down

flat

and so if I think of this triangle let's

make that green and in fact um let's

just shade it in this triangle

here the legs of the triangle are L and

W just like they were here so the

distance across the floor let's call

that distance

X as this uh becomes a leg of the

vertical uh triangle so we have a

two-step process start with L and W and

I can say x is equal to the square < TK

of l^2 +

w^2 this is good we'll just use green to

refer to this

triangle and um uh what we're then going

to want to do is find use that X as a

leg of the red triangle so let's switch

to red

now and for this red triangle we want uh

D which is the hypotenuse is the square

< TK of x^2 +

h^2

okay so what is

X2 well here is

X if I take X

squar that's going to be uh if I take

the square root of something and I turn

around and square it it's like undoing

the square root so that's simply l s

+

w^2 and so I can substitute

this for my x^2 let's see what we get D

equals the square < TK of X2 which is

this plus

h^2 now that is rather remarkable look

what we have we have a new formula that

looks a a lot like the Pythagorean

theorem the diagonal across a rectangle

in two Dimensions is simply the square

root of l^ 2 +

w^2 the diagonal three-dimensionally

across a three-dimensional room is the

square < TK of l^2 + w^2 +

h^2 so it's like an

extension okay so if we have

a uh say a rectangle like this and if

the width in this direction is say three

and the distance in this way is five and

the distance this way is

two let's pull up a

calculator and we can just do it all

right here I take 3 squared so I'll take

3^

squared

plus 5^ squar 5^ s let's say equals

plus 2

squ

equals 38 and then take the square root

so I take the length the width and the

height Square each of them add them

together and take the square root so the

diagonal

here is going to be

6.16 in whatever units we're measuring

and if these are feet that'll be 6.16

feet

okay so this is a useful extension of

the Pythagorean theorem we now have

something that looks a lot like the

Pythagorean theorem but it's a a

three-dimensional

version okay in Algebra 1 uh you learned

how to find equations of lines and

that's about as far as you got you

really didn't find equations of lots of

different things on the plane but from

what we've learned so far it's very easy

to find the equation of a circle so here

is a grid

and here's a circle whose radius is four

so let's say radius equals 4 and so the

question is can I find an equation that

describes this circle and it's

remarkably simple to do that let's see

what we're talking about pick any point

on the circle label it

XY okay in fact XY could stand for any

point in the plane but I want to say

what is the condition so that the XY

point that I picked is actually on the

circle and so you have to say what do

you mean when you talk about a circle if

I drew a circle with a compass I'd put

the point of the compass here and then

stretch it out to a certain distance as

a radius and then swing it around what

I'm physically doing with the compass is

locating on the plane all the points

that are a given distance this radius

from this point so I'm saying this

distance is going to be my radius and

any point on the plane that is this

distance from the center point is going

to be on the

circle well let's try it look at this hm

that's a diagonal line and notice if I

drop a perpendicular here and go over

there I have a right triangle and in

fact the XY Point here tells how far

over and how far up I have to go to get

from the origin up to here so this side

of the triangle is actually X and this

side of the triangle is actually Y and

then I can write down the relation among

these three variables by noticing X and

Y are the legs of a right triangle and R

is the hypotenuse so R 2 is equal to

x^2 +

y^2 in fact what we have here is an

equation that describes the circle any

point for which the X and Y coordinates

of the point satisfy this relationship

will be on the

circle okay let's try out this equation

of a circle in

geogebra so down here I'm going to input

x^2 Plus y^2

equals and then it's going to be R 2 so

let's pick a radius what if I wanted

this circle to have a radius of 2 so I

want it to be this big okay well uh x^2

+ y^2 = R2 so I'm going to type 2^2 or

simply four and let's see what we get

there we are we have a circle of the

given radius and notice over here in the

algebra view that's why they call it Geo

jebra it's algebra and geometry combined

it says x^2 + y^2 = 4 and that's the

equation for this circle if I turn off

this circle it disappears right you can

click this little um ball out in front

of the C and so there you have it

okay if I change this to be

X2 +

y^2 equals and some other amount like

let's say 1 which is 1^ squar we expect

to get a circle that's in here and sure

enough what if I want for equation with

radius of three then I'm going to say

x2+

y^2

equals uh I have remember I have to say

3^ squar so it' be

9 and there we go so you can make a

Target so when we specify these things

algebraically we now know how to specify

a circle what if using geogebra I simply

put this uh uh Center Point

here and then pull it out and go out to

say the

four okay this time I specified the

circle geometrically by using the

geometry tools here

but look what it put over here on the

algebra view of the program it says x^2

+ y^2 = 16 so we didn't enter the

equation it used the equation to

actually uh compute the circle and

figure out which pixels on the screen

it's going to turn blue here or whatever

this color is and it's going to be

determined by x^2 + y^2 ALS r^2 where R

is 4 okay so in the background uh

programs like Photoshop and other kinds

of uh graphic manipulation programs are

doing this kind of thing all the time

and if you're a a graphic artist or U

say a a commercial artist so forth you

would you need to have some appreciation

for what's going on behind the scenes to

be able to use the tools well a lot of

times you don't have to use the algebra

directly but uh somebody's doing that

and those people I'm sure getting paid

very well okay there you have it uh

equations not only of straight lines but

we've moved on to equations of other

objects in this case circles because

circles are defined in terms of the

distance from a center point out to the

circle and we know how to find distances

between points on the

plane so we found uh three different

extensions or if you want to call them

applications of the Pythagorean theorem

here we have the distance

formula we have an extension of the

Pythagorean theorem into three

dimensions and now we found how to use

distance as a way of defining um curves

that we can put on graphs in this case a

circle okay