Graad 11 Meetkunde
Summary
TLDRThe video script is an educational lecture focusing on geometric concepts related to circles and chords. It discusses the properties of chords and circles, including the definition of a chord as a line segment with endpoints on the circumference of a circle. The script introduces the concept of the perpendicular bisector of a chord, which passes through the center of the circle, and its importance in circle geometry. It also covers the Pythagorean theorem in the context of circles and chords, using it to calculate the radius of a circle given the lengths of a chord and its perpendicular bisector. The lecture includes examples to illustrate these concepts and emphasizes the importance of understanding and being able to prove these theorems.
Takeaways
- 📐 The script discusses the properties of chords and circles, focusing on the relationship between the endpoints of chords and the circumference of circles.
- 🔴 It introduces the concept of the perpendicular bisector of a chord, which passes through the center of the circle, a key property involving the circle's center.
- 📏 The script explains that the perpendicular bisector of a chord is also a radius of the circle, which is an important theorem to learn and prove.
- 🔺 The script mentions the converse of the theorem, which states that if a line passing through the center of a circle is perpendicular to a chord, then it bisects the chord.
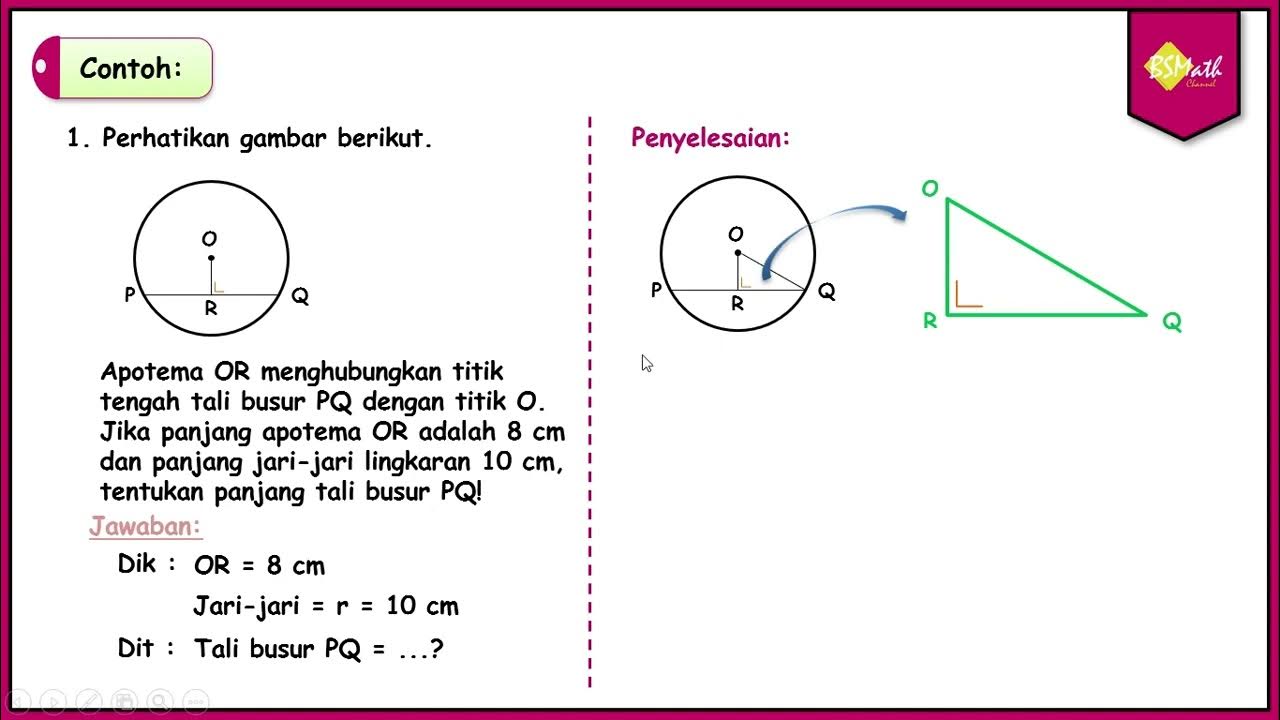
- 📘 The script provides an example problem involving the calculation of the radius of a circle given the lengths of a chord and a perpendicular segment.
- 🧮 It uses the formula \( \pi r = \text{length of the chord} \) to solve for the radius, demonstrating the application of the circle's circumference formula.
- 🔍 The script also discusses the use of the Pythagorean theorem to find the lengths of segments in right-angled triangles formed by chords and radii.
- 📐 It provides a step-by-step approach to solving problems involving the properties of circles and chords, emphasizing the importance of understanding the theorems and their proofs.
- 📝 The script concludes with a summary of the steps and concepts covered, reinforcing the importance of following the steps and applying the theorems correctly.
- 🔗 The discussion is aimed at helping learners understand and apply the properties of circles and chords, with an emphasis on the practical application of theorems in geometry.
Q & A
What is the main topic discussed in the script?
-The main topic discussed in the script is geometry, specifically focusing on circles, chords, and the properties of the diameter and radius in relation to the circumference of a circle.
What is the significance of the diameter in the context of the script?
-The diameter is significant because it passes through the center of the circle and is twice the length of the radius. It is also used to calculate the circumference of a circle using the formula C = πd.
What is the relationship between the diameter and the circumference of a circle as mentioned in the script?
-The circumference of a circle is directly proportional to its diameter. The script implies that the circumference is the product of the diameter and π, which is a fundamental property of circles.
What property of a circle is discussed in relation to chords and the center?
-The script discusses that the perpendicular bisector of a chord passes through the center of the circle, which is a key property used in various geometric proofs and calculations.
How does the script describe the process of proving a statement?
-The script suggests that to prove a statement, one must learn how to apply certain theorems and properties, such as the relationship between the diameter and the circumference of a circle.
What is the role of the perpendicular bisector in the script's discussion of circles?
-The perpendicular bisector of a chord is crucial as it always passes through the center of the circle, which is a key concept used in the script to solve problems related to the geometry of circles.
What is the significance of the radius in the script's discussion?
-The radius is significant as it is the distance from the center of the circle to any point on the circle's circumference. It is used to calculate the diameter and the circumference of the circle.
How is the length of the radius related to the length of the diameter in the script?
-The length of the radius is half the length of the diameter, as stated in the script, which is a fundamental geometric property of circles.
What is the formula used in the script to calculate the circumference of a circle?
-The script uses the formula C = πd to calculate the circumference of a circle, where C is the circumference and d is the diameter.
How does the script use the properties of a circle to solve for the length of a chord?
-The script uses the properties of a circle, such as the perpendicular bisector of a chord and the Pythagorean theorem, to solve for the length of a chord by relating it to the radius and diameter of the circle.
What is the purpose of the examples given in the script?
-The examples in the script serve to illustrate how to apply geometric properties and theorems to solve practical problems, such as finding the radius or the length of a chord in a circle.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)