CS101 2 Module 3 Relations and their Properties PART1
Summary
TLDRThis module delves into the concept of relations in mathematics, focusing on their properties and applications. It introduces relations as subsets that denote possible connections between elements within or across sets. The module explains three key properties of relations: reflexivity (a relation to oneself), symmetry (reciprocal relationships), and transitivity (a chain of relationships leading to a direct connection). Examples using equality, inequality, and less-than operators illustrate these concepts, with closure ensuring all possible relations within a set are considered.
Takeaways
- 🔑 Relations are a mathematical concept used to explore the relationships among elements within or between sets.
- 🧩 A relation is denoted as a subset of a set cross its own set (x x), indicating the potential relationships between elements.
- 🔍 The module's objective is to understand the properties of relations and apply them to solve problems.
- 🔄 Relations can exist between elements of the same set or between elements of different sets.
- 🔄 Reflexive property: For all elements x in a set, x is related to itself. An example is the equality operator.
- 🔄 Symmetric property: If x is related to y, then y is also related to x. An example is the not-equal operator.
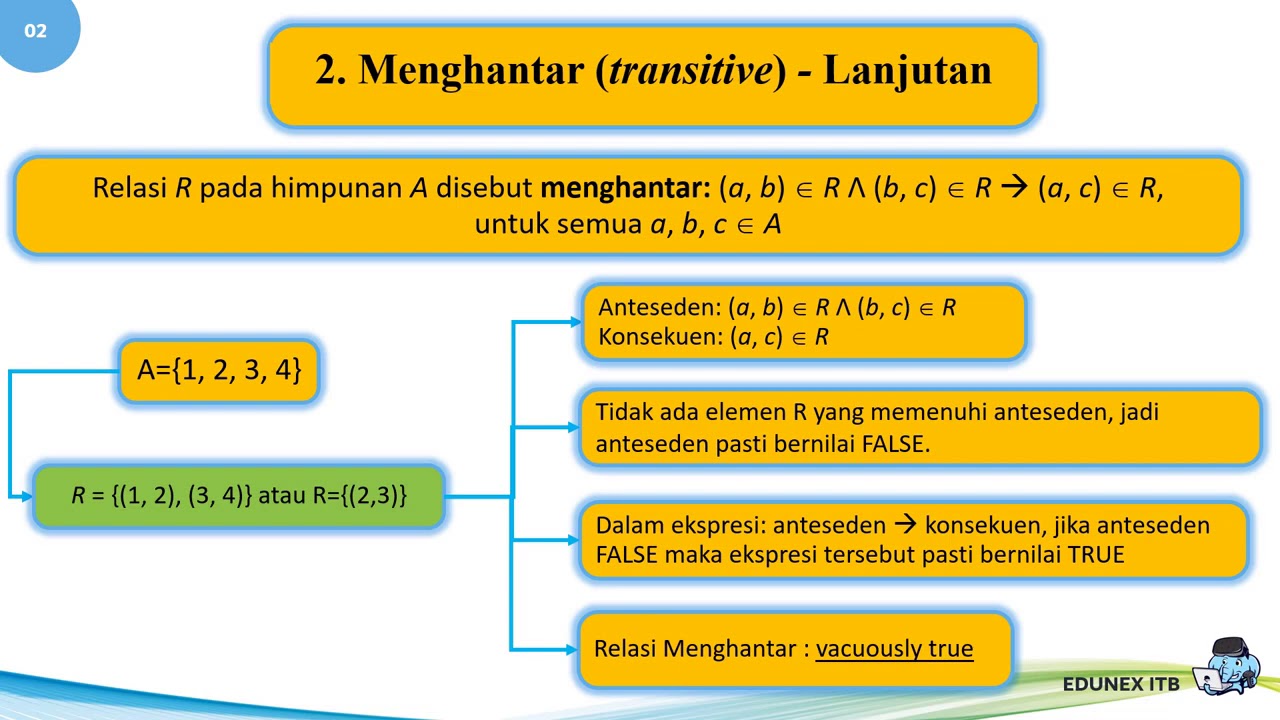
- 🔄 Transitive property: If x is related to y, and y is related to z, then x is also related to z. An example is the less-than operator.
- 🔄 Closure in transitivity refers to completing all possible relations within a set to ensure all expected shortcuts are present.
- 📊 Graphical representation of relations helps visualize the relationships and understand properties like reflexivity, symmetry, and transitivity.
- 📚 The script uses examples of mathematical operators to illustrate the properties of relations, making abstract concepts more tangible.
Q & A
What is the main objective of the module discussed in the transcript?
-The main objective of the module is to understand relation properties and solve problems involving relations.
What is a relation in the context of sets?
-A relation is a subset of a Cartesian product of a set with itself, denoted as r on a set x, which represents the possibility of elements in the set having a relationship.
How is a relation denoted?
-A relation can be denoted as 'x r y', meaning that element x is related to element y, or sometimes written as 'r(x, y)' if the relation is also considered a function.
What are the three basic properties of a relation?
-The three basic properties of a relation are reflexivity, symmetry, and transitivity.
How is reflexivity defined in the context of relations?
-Reflexivity is defined as a property where for all elements x in a set, x is related to itself (x r x).
What is an example of a reflexive relation?
-An example of a reflexive relation is the equality operator, where for any element x in a set, x equals x is always true.
How is symmetry defined in the context of relations?
-Symmetry is defined as a property where if x is related to y (x r y), then y must also be related to x (y r x).
What is an example of a symmetric relation?
-An example of a symmetric relation is the not equal operator, where if x is not equal to y, then y is also not equal to x.
How is transitivity defined in the context of relations?
-Transitivity is defined as a property where if x is related to y (x r y) and y is related to z (y r z), then x must also be related to z (x r z).
What is an example of a transitive relation?
-An example of a transitive relation is the less than operator, where if x is less than y and y is less than z, then x is also less than z.
What is meant by the term 'closure' in the context of transitivity?
-The term 'closure' refers to completing all possible relations within a given set to ensure that all expected shortcuts or direct relations between elements are present.
How does the concept of closure relate to the transitivity property?
-Closure ensures that the transitivity property is fully realized by creating direct relations (shortcuts) between elements that are indirectly related through a series of other relations.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
5.0 / 5 (0 votes)