Position Vectors and Displacement Vectors - Physics
Summary
TLDRThis video tutorial explains the concept of position vectors and their application in calculating displacement vectors. It starts with a 2D example, showing how to find the position vector from the origin to a point (3,2), represented as 3i + 2j. The tutorial then extends to 3D, illustrating how to determine the position vector for a point (3,4,5), expressed as 3i + 4j + 5k. It further discusses how to calculate the magnitude of a vector using the square root of the sum of squares of its components. Finally, it demonstrates how to find the displacement vector when a particle moves from point A (2,3,4) to point B (5,-2,8), by subtracting the initial position vector from the final one.
Takeaways
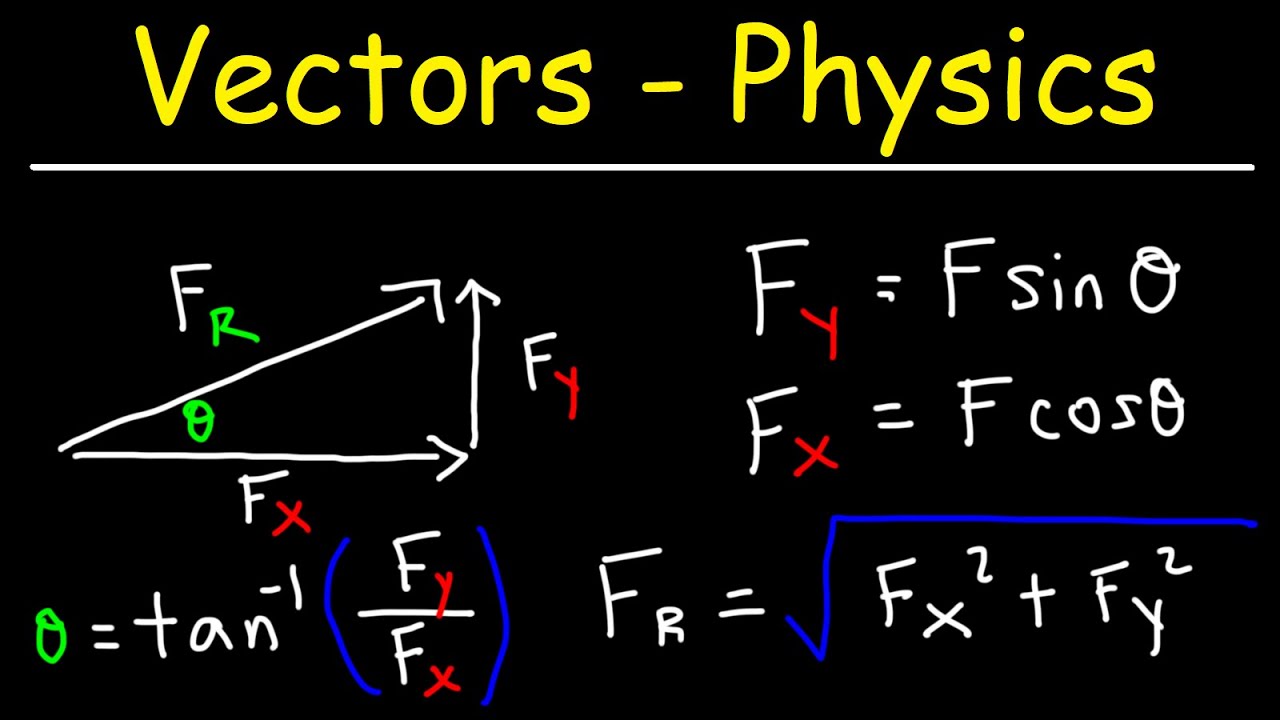
- 📝 Position vectors are vectors that start from the origin and point to a specific point in space.
- 📝 The position vector for a point P(3, 2) in a 2D coordinate system is represented as 3i + 2j, indicating the direction and distance from the origin to point P.
- 📝 In a 3D coordinate system, a position vector for a point P(3, 4, 5) is represented as 3i + 4j + 5k, showing the x, y, and z components of the vector.
- 📝 The magnitude or length of a position vector in a 2D system is calculated using the formula √(x^2 + y^2), while in 3D it's √(x^2 + y^2 + z^2).
- 📝 The magnitude of the position vector for point P(3, 4, 5) is √(3^2 + 4^2 + 5^2) = √(50) = 5√2.
- 📝 Displacement vector is calculated by subtracting the initial position vector from the final position vector, representing the change in position.
- 📝 For a particle moving from point A(2, 3, 4) to point B(5, -2, 8), the displacement vector is found by subtracting the position vector of A from B.
- 📝 The displacement vector from A to B is calculated as (5i - 2j + 8k) - (2i + 3j + 4k) = 3i - 5j + 4k.
- 📝 The video provides a resource for further learning with an ebook on passing math and science classes available at video.tutor.net.
- 📝 The first chapter of the ebook can be obtained for free by joining the email list mentioned in the video.
Q & A
What are position vectors?
-Position vectors are vectors that start from the origin and point to a particular point in a coordinate system. They are represented by the symbol 'r' with a vector symbol attached to it.
How do you draw a position vector for a point in a 2D coordinate system?
-To draw a position vector for a point in a 2D coordinate system, you draw it from the origin to the point of interest, using the x and y coordinates of the point.
What is the position vector for a point P with coordinates (3, 2) in a 2D coordinate system?
-The position vector for point P with coordinates (3, 2) in a 2D coordinate system is 3i + 2j, where 3i represents the x-component and 2j represents the y-component.
How do you calculate the position vector in a 3D coordinate system?
-In a 3D coordinate system, the position vector is calculated by traveling along the x, y, and z directions from the origin to the point of interest, using the x, y, and z coordinates of the point.
What is the formula to find the magnitude of a position vector in a 2D coordinate system?
-The magnitude of a position vector in a 2D coordinate system is found using the formula: √(x² + y²), where x and y are the components of the vector.
How do you find the magnitude of a position vector in a 3D coordinate system?
-The magnitude of a position vector in a 3D coordinate system is calculated using the formula: √(x² + y² + z²), where x, y, and z are the components of the vector.
What is the displacement vector and how is it different from a position vector?
-The displacement vector represents the change in position of an object as it moves from one point to another. It is different from a position vector because it is the difference between two position vectors.
How do you calculate the displacement vector when a particle moves from point A to point B?
-To calculate the displacement vector when a particle moves from point A to point B, you subtract the position vector of point A from the position vector of point B: R_B - R_A.
What is the position vector for point A with coordinates (2, 3, 4) in a 3D coordinate system?
-The position vector for point A with coordinates (2, 3, 4) in a 3D coordinate system is 2i + 3j + 4k.
What is the position vector for point B with coordinates (5, -2, 8) in a 3D coordinate system?
-The position vector for point B with coordinates (5, -2, 8) in a 3D coordinate system is 5i - 2j + 8k.
How do you find the displacement vector when a particle moves from point A to point B with given coordinates?
-To find the displacement vector from point A to point B, calculate the difference between their position vectors: (5i - 2j + 8k) - (2i + 3j + 4k), which results in 3i - 5j + 4k.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)