O que são VETORES?

Summary

This video introduces the concept of vectors in physics, explaining their key components: magnitude, direction, and sense. It demonstrates how vectors are used to represent quantities like force, velocity, and displacement. The video covers how to perform vector addition and subtraction, including the use of the Pythagorean theorem for vectors in perpendicular directions. A practical example involving a ship's navigation illustrates how to calculate the resultant vector, helping viewers understand the real-world application of vector operations.

Takeaways

• 😀 Vectors help understand motion, forces, and many other concepts in physics.
• 😀 A vector represents magnitude, direction, and sense of a physical quantity, such as force, velocity, acceleration, and displacement.
• 😀 Vectors are represented by a line segment with an arrow at one end, denoted by a letter and a small arrow above it.
• 😀 The magnitude of a vector, also known as its intensity, is its numerical value followed by the unit of measurement (e.g., meters, newtons).
• 😀 The length of a vector is proportional to its magnitude, meaning a longer vector represents a larger magnitude.
• 😀 Direction refers to the inclination of the vector, and there are three types of directions: vertical, horizontal, and oblique.
• 😀 The sense of a vector is shown by its arrow, and the same direction can have opposite senses, such as up/down or left/right.
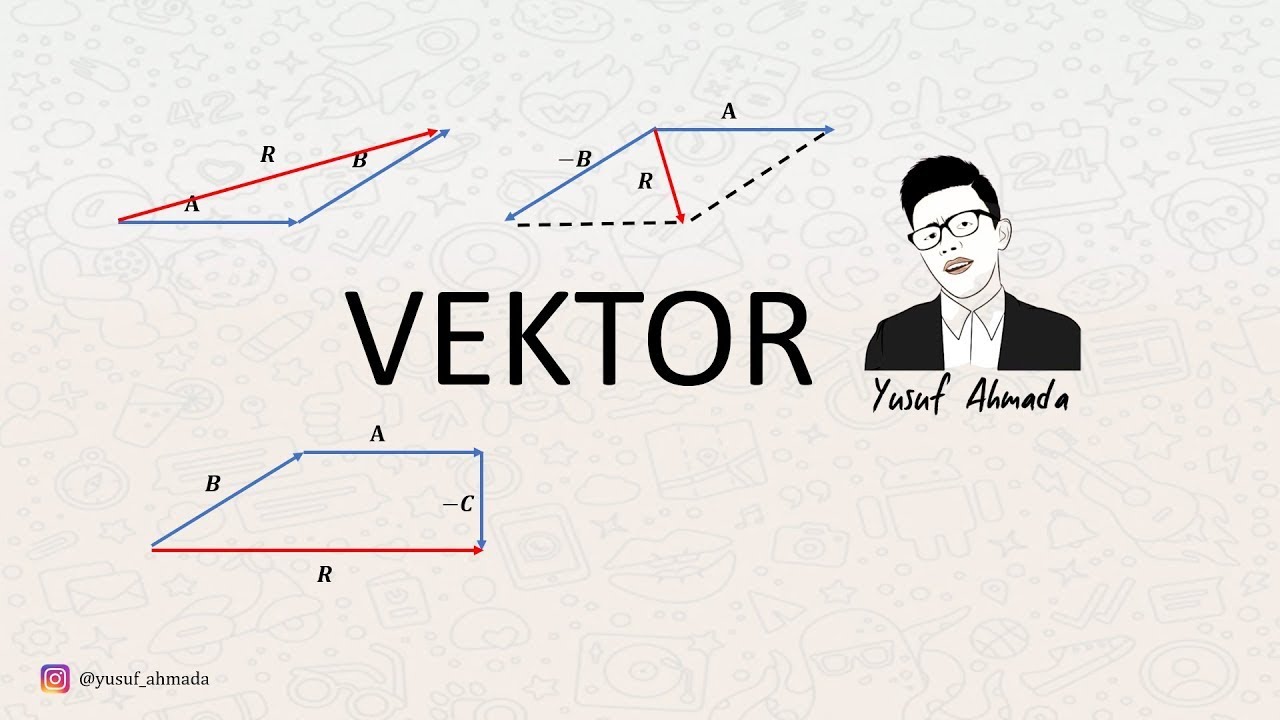
• 😀 In a system with multiple forces, the resulting vector represents the net effect of these forces, found by vector addition and subtraction.
• 😀 The result of forces acting on a body can be represented by a single resultant vector, which shows the overall direction of motion.
• 😀 When two vectors are perpendicular, the resultant vector is determined using the Pythagorean theorem, where the magnitude is the hypotenuse of a right triangle.
• 😀 For vectors with the same direction and opposite sense, their magnitudes are subtracted to find the resultant vector, keeping the direction of the larger one.

Q & A

What is a vector in physics?

A vector is a representation that determines the magnitude, direction, and sense of a vector quantity. It is shown as a directed line segment, with a start and end point, usually denoted by a letter with an arrow above it.

Why are vectors important in understanding physical quantities?

Vectors are crucial because they represent physical quantities that need both a magnitude and direction, such as force, velocity, acceleration, and displacement. These quantities cannot be fully understood by just a numerical value; their direction of application also needs to be considered.

What is the magnitude (or modulus) of a vector?

The magnitude of a vector is its numerical value, representing the intensity or size of the quantity it represents. It is expressed with the value followed by the unit of measure. For example, a vector representing displacement may have a magnitude of 2 meters.

How is the magnitude of a vector visually represented?

The magnitude is visually represented by the length of the vector. A longer vector represents a larger magnitude, while a shorter vector represents a smaller magnitude.

What is the importance of direction and sense in a vector?

The direction of a vector refers to the orientation of the line segment representing it (e.g., vertical, horizontal, or oblique), while the sense indicates the direction of the vector along that line (e.g., upwards, downwards, left, or right). Both are essential to fully describe the vector.

What does it mean when two vectors have opposite directions?

When two vectors have the same direction, their magnitudes are simply added. However, when vectors have opposite directions, their magnitudes are subtracted, and the resultant vector's direction will be that of the larger vector.

How do you calculate the resultant vector of multiple forces?

The resultant vector is found by performing vector operations such as addition and subtraction. If the vectors are aligned in the same or opposite directions, their magnitudes are added or subtracted. If they have perpendicular directions, the Pythagorean theorem is used to calculate the magnitude of the resultant.

How does the Pythagorean theorem apply to vectors with perpendicular directions?

For two vectors with perpendicular directions, the magnitude of the resultant vector is calculated using the Pythagorean theorem. If the vectors are represented by 'a' and 'b', the resultant vector's magnitude 'r' is given by the formula r = √(a² + b²).

How would you find the resultant vector of two vectors at right angles to each other?

To find the resultant of two perpendicular vectors, you use the Pythagorean theorem. For example, if one vector has a magnitude of 12 km and the other 5 km, the resultant magnitude is √(12² + 5²) = √169 = 13 km.

What is the application of vector addition in real-life scenarios?

In real life, vector addition is used in scenarios like calculating the net displacement of a moving object. For instance, a ship might travel in a straight line north and then turn west. The overall displacement can be calculated by adding these two displacement vectors, which gives the shortest path to its destination.