Área bajo la curva por Extremos Derechos
Summary
TLDREn este video se explica cómo calcular el área bajo una curva en un intervalo específico utilizando el método de los rectángulos. Se toma la función f(x) = x^2 + 1 y se determina su área bajo la curva en el rango [-3, 3] con 6 rectángulos. Se detalla cómo se calcula el delta x, se grafican los puntos correspondientes y se suman las áreas de los rectángulos por extremos derechos para obtener una aproximación del área total, que resulta ser 25 unidades cuadradas.
Takeaways
- 📊 El objetivo es calcular el área bajo la curva de la función f(x) = x^2 + 1 en el intervalo cerrado de -3 a 3 utilizando 6 rectángulos.
- 📐 La función f(x) es una parábola que se describe en el guion y se visualiza en el video.
- 📈 Se utiliza el método de los rectángulos para aproximar el área bajo la curva, eligiendo 6 rectángulos para cubrir el intervalo dado.
- 🔢 El cálculo de la base de los rectángulos se realiza mediante la fórmula Δx = (b - a) / n, donde a = -3, b = 3, y n = 6.
- 📝 Se establece que la base de cada rectángulo es de 1 unidad, ya que el intervalo se divide en 6 partes iguales.
- 📉 Los valores de x para los rectángulos son -3, -2, -1, 0, 1, 2, y 3, correspondiendo a los puntos de evaluación de la función.
- 📌 Se calculan los valores de la función f(x) para cada punto de x, y se establecen las alturas de los rectángulos correspondientes.
- 📐 Se grafican los puntos obtenidos y se conectan para visualizar la aproximación de la parábola.
- 📏 Se calcula el área de cada rectángulo individualmente, multiplicando la base por la altura correspondiente.
- 🔢 El área total aproximada se obtiene sumando el área de todos los rectángulos, resultando en 25 unidades cuadradas.
Q & A
¿Qué método se utiliza para encontrar el área bajo la curva en el ejemplo proporcionado?
-Se utiliza el método de los rectángulos, donde se divide el área en segmentos rectangulares para calcular la aproximación del área bajo la curva.
¿Cuál es la función f(x) que se está analizando en el ejemplo?
-La función que se está analizando es f(x) = x^2 + 1.
¿Cuál es el intervalo de análisis para el área bajo la curva en el ejemplo?
-El intervalo de análisis es el cerrado desde -3 hasta 3.
¿Cuántos rectángulos se utilizan para aproximar el área en el ejemplo?
-Se utilizan 6 rectángulos para aproximar el área bajo la curva.
¿Cómo se calcula el valor de Δx (delta x) para los rectángulos?
-El valor de Δx se calcula como (b - a) / n, donde b es el valor final del intervalo, a es el valor inicial y n es el número de rectángulos.
¿Cuál es la base de los rectángulos utilizados en el cálculo del área?
-La base de los rectángulos es de 1 unidad, ya que el intervalo se divide en 6 partes iguales.
¿Cómo se determina la altura de cada rectángulo en el método de los rectángulos?
-La altura de cada rectángulo se determina sustituyendo el valor de x en la función f(x) y calculando el resultado.
¿Qué significa 'extremos derechos' y cómo se relaciona con el cálculo del área?
-Extremos derechos significa que se toma la altura del rectángulo desde el valor actual de x hasta el siguiente valor de x, lo que se utiliza para calcular la aproximación del área bajo la curva.
¿Cuál es la fórmula general para calcular el área de un rectángulo en este contexto?
-La fórmula general para calcular el área de un rectángulo es base por altura, donde la base es el intervalo y la altura es el valor de la función en ese intervalo.
¿Cómo se calcula el área total aproximada bajo la curva utilizando el método de los rectángulos?
-El área total aproximada se calcula sumando el área de cada uno de los rectángulos, que es la base (1 unidad) multiplicada por la altura correspondiente de cada rectángulo.
¿Cuál es el resultado final del área bajo la curva utilizando el método de los rectángulos con 6 rectángulos?
-El área total aproximada bajo la curva es de 25 unidades cuadradas.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Método: rectángulos CIRCUNSCRITOS | Área bajo la curva | Cálculo Integral

Cálculo Integral 01:Área bajo una curva. Area under a curve

Área bajo la curva (Cálculo integral) Método de rectángulos. EJEMPLO 2

Área bajo la curva por extremos izquierdos

Área bajo la curva (Cálculo integral) Método de rectángulos. EJEMPLO 1
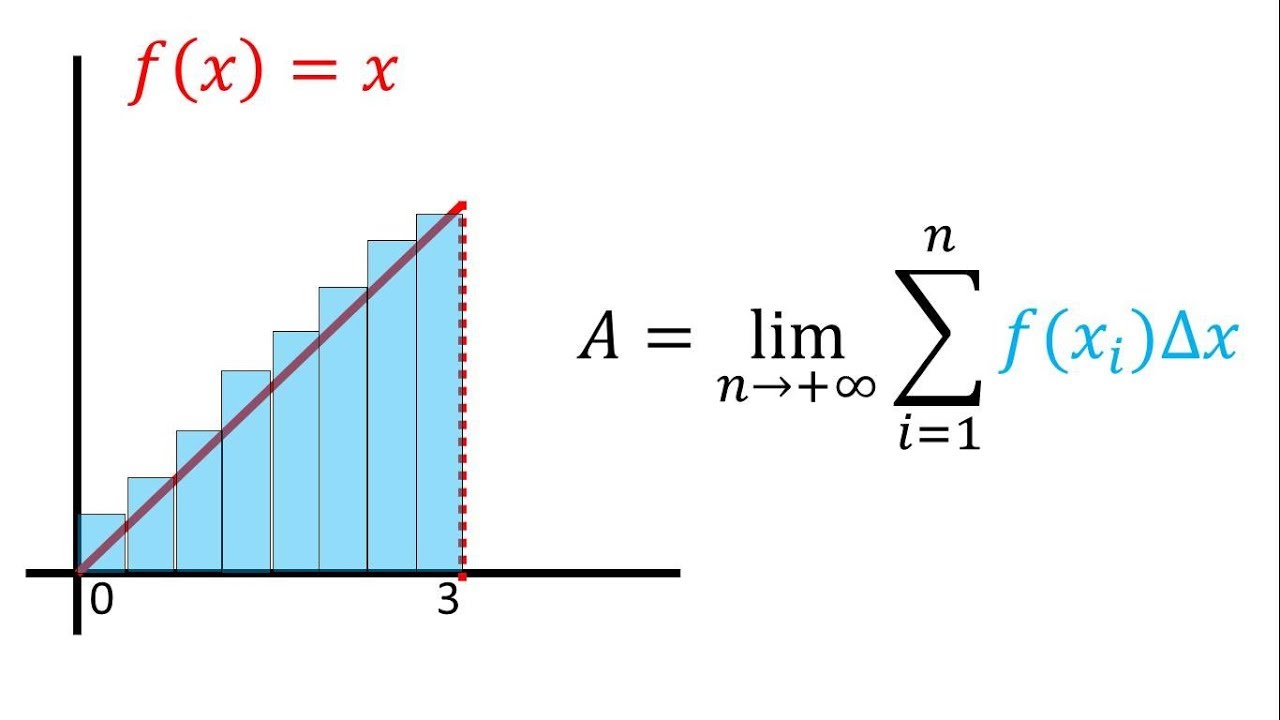
Área de una región plana utilizando sumatorias
5.0 / 5 (0 votes)
