The million dollar equation (Navier-Stokes equations)
Summary
TLDRThis video delves into the Navier-Stokes equations, fundamental for modeling fluids like water and air. These equations, part of the Millennium Prize Problems, remain unsolved in some areas despite their importance in weather forecasting, aerodynamics, and fluid dynamics. The video explains key assumptions like fluids being Newtonian, incompressible, and isothermal, and breaks down the equations based on physical laws like conservation of mass and Newton's second law. The challenge lies in proving smooth solutions for these chaotic equations, especially in predicting turbulence and long-term fluid behavior.
Takeaways
- 💧 The Navier-Stokes equations are fundamental in describing the motion of fluids, including water, air, and honey.
- 🏆 These equations are part of the Millennium Prize Problems, with a $1,000,000 prize for anyone who can solve them.
- 🔍 The script introduces the Navier-Stokes equations by considering a flowing lake and the challenge of predicting its behavior over time.
- 🌟 The equations are based on assumptions that the fluid is Newtonian, incompressible, and isothermal.
- 🔄 The first Navier-Stokes equation represents the conservation of mass within the fluid, implying that the divergence of the velocity vector field must be zero.
- ⚖️ The second equation is a fluid dynamics version of Newton's second law, relating the forces acting on a fluid element to its density and acceleration.
- 💨 Forces considered in the equations include pressure, viscosity (internal forces), and external forces like gravity.
- 🌀 The equations are known for their chaotic nature, which makes long-term predictions and smooth solutions difficult, affecting weather forecasting and fluid dynamics.
- 🚀 Despite their complexity, Navier-Stokes equations are crucial for modeling aerodynamics in objects like airplanes and cars.
- 🌡️ The script also touches on the limitations of the equations in predicting fluid behavior, especially in turbulent conditions.
Q & A
What are the Navier-Stokes equations used for?
-The Navier-Stokes equations are used to describe the motion of fluids and are applied in fields like weather forecasting, designing airplanes and rockets, and predicting water currents.
Why are the Navier-Stokes equations considered one of the Millennium Prize Problems?
-The Navier-Stokes equations are part of the Millennium Prize Problems because, despite their extensive use, there are still unsolved mathematical issues related to their existence and smoothness. Proving a smooth solution for all conditions could earn a million-dollar prize.
What does it mean for a fluid to be Newtonian?
-A Newtonian fluid is one in which the viscosity remains constant, regardless of the rate of shear stress applied. For example, water and air are Newtonian fluids, while ketchup, whose viscosity decreases with shear, is not.
What assumptions are made about the fluid in the video?
-Three assumptions are made: the fluid is Newtonian (its viscosity is not affected by shear rate), incompressible (its volume doesn’t change under pressure), and isothermal (there is no heat loss as it flows).
What does the first Navier-Stokes equation describe?
-The first Navier-Stokes equation ensures the conservation of mass in the fluid. Mathematically, it states that the divergence of the velocity field must be zero, meaning no mass is lost or created at any point in the fluid.
How does the second Navier-Stokes equation relate to Newton's second law?
-The second Navier-Stokes equation is derived from Newton's second law, stating that the forces acting on a fluid molecule equal its mass times acceleration. It incorporates pressure, viscosity, and external forces like gravity.
Why is turbulence an issue when solving the Navier-Stokes equations?
-Turbulence introduces chaotic behavior in fluid flows, meaning small changes in initial conditions can lead to large variations in outcomes. This makes long-term predictions difficult and is one of the reasons why solving the Navier-Stokes equations is so challenging.
What is meant by a 'smooth' solution to the Navier-Stokes equations?
-A 'smooth' solution refers to a solution that is continuously differentiable. In other words, it does not have any abrupt changes or discontinuities, which would make the equations easier to predict and model.
How do pressure and viscosity affect the movement of fluids, according to the Navier-Stokes equations?
-Pressure causes fluid to move from areas of high pressure to low pressure, while viscosity resists motion, causing friction between fluid molecules. These forces are key components in the Navier-Stokes equations.
Why can’t we predict weather or airplane turbulence accurately for long periods using the Navier-Stokes equations?
-The chaotic nature of fluid flow, especially turbulence, makes long-term predictions highly sensitive to initial conditions. Even with the Navier-Stokes equations, this complexity limits accurate predictions to short time frames.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
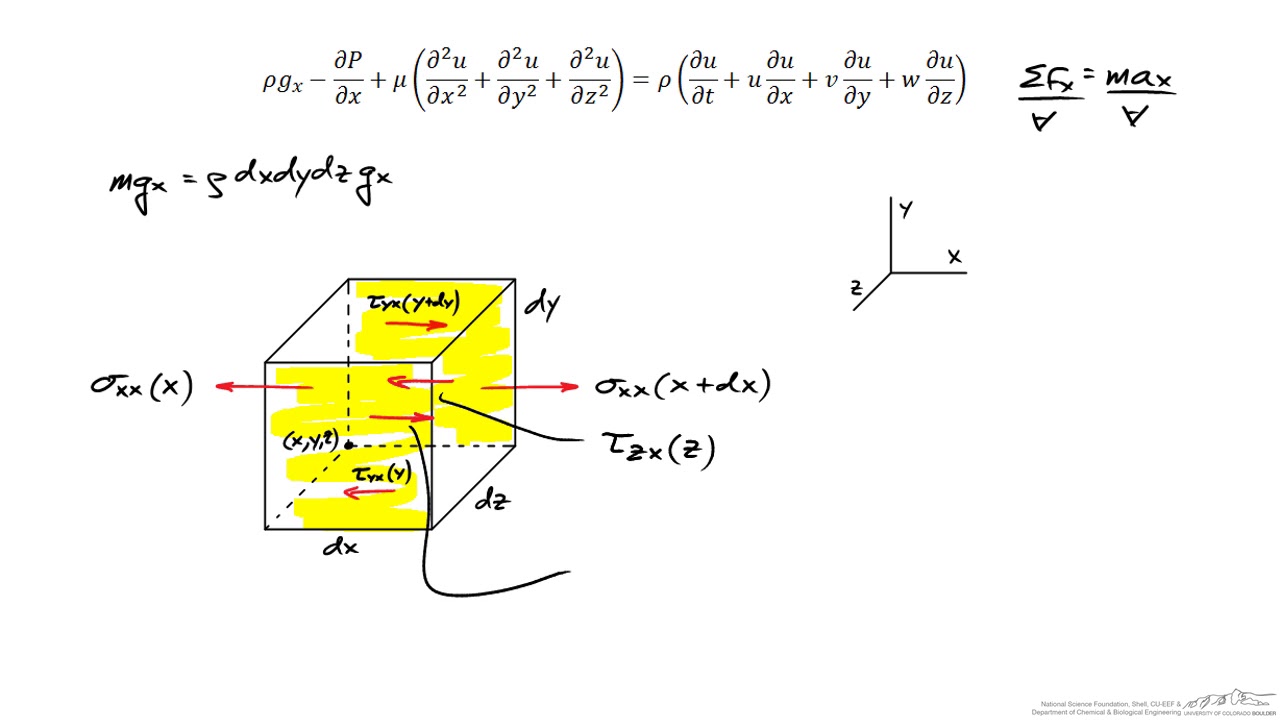
Description and Derivation of the Navier-Stokes Equations

LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 3
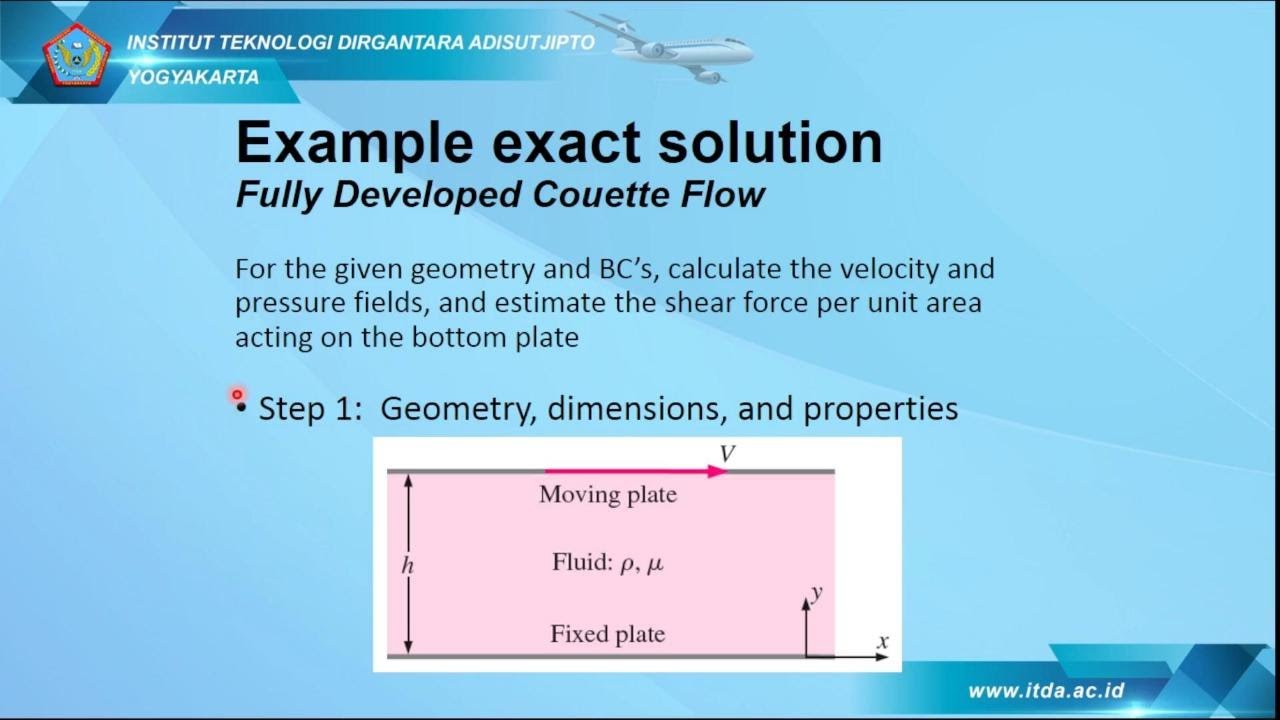
LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 4

Solve This Mathematics Problem and Get 1 Million Dollars

LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 1

Dimensionless Parameters — Lesson 2
5.0 / 5 (0 votes)
