LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 1
Summary
TLDRThis script discusses differential analysis in fluid flow, covering the derivation of differential equations for fluid motion, including the continuity equation and Newton's second law or Navier-Stokes equations. It explains how these equations are used to solve flow details across a domain but are often complex, requiring computational assistance. The script introduces stream functions and streamlines, aiming to help understand mass conservation equations, calculate stream functions, and plot flow lines for known velocity fields. It also touches on the use of differential analysis for overall flow analysis, such as calculating forces on objects in fluid flow.
Takeaways
- 📚 The chapter focuses on differential equations for fluid flow, including the continuity equation and Newton's second law or Navier-Stokes equations.
- 💡 These equations are applicable to every point within a flow field, allowing for the solution of flow details across the entire flow domain.
- 🖥️ Most differential equations in fluid mechanics are complex and often require computer assistance for solutions.
- 🔍 The equations sometimes need to be combined with others, such as state equations and energy or transport equations.
- 📝 A step-by-step procedure is provided for solving a series of differential equations for fluid motion and obtaining analytical solutions for simple examples.
- 🌐 Concepts like stream function and stream lines are introduced, which are essential for understanding flow patterns in two-dimensional flow fields.
- 🔧 The chapter aims to help understand how to derive differential equations for mass and momentum conservation, calculate stream functions, and plot flow lines for known velocity fields.
- 🎯 After studying the chapter, one should be able to derive analytical solutions for simple flow problems and understand the overall flow analysis, such as flow rate and force acting on objects.
- 🌀 Differential analysis involves applying fluid motion differential equations to each point in a flow field, known as the domain.
- 📉 The process involves considering the flow field as a collection of tiny control volumes, which when solved, yield detailed flow properties at each point.
- 📊 The chapter also explains how to derive the differential form of the mass conservation equation using the divergence theorem and differential volume methods.
Q & A
What are the main differential equations discussed in the chapter for fluid flow?
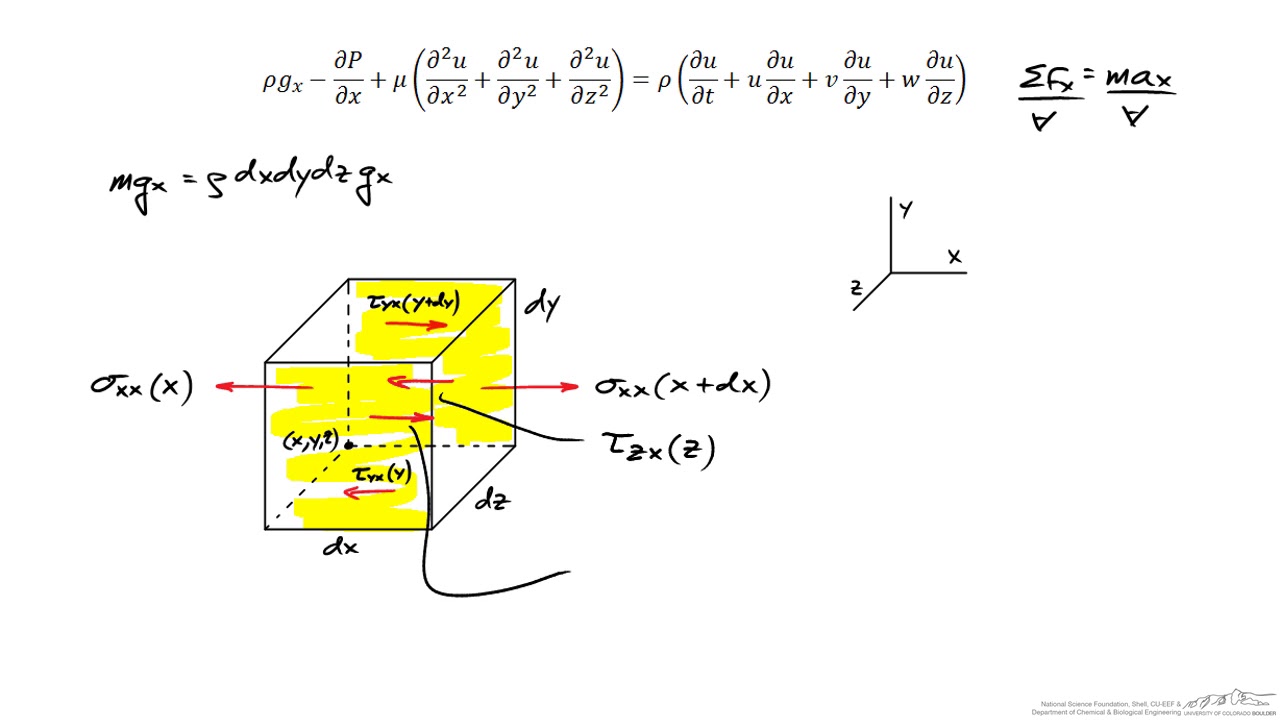
-The main differential equations discussed in the chapter are the continuity equation (conservation of mass) and the Navier-Stokes equation (Newton's second law), which are used to describe the motion of fluid at every point within a flow field.
Why are most differential equations in fluid mechanics difficult to solve?
-Most differential equations in fluid mechanics are difficult to solve because they are often complex and require computational assistance. Additionally, they may need to be coupled with other equations such as state and energy equations or transport equations.
What is the purpose of the step-by-step procedure given in the chapter?
-The step-by-step procedure is provided to guide the reader through solving a series of differential equations that describe fluid motion and to obtain analytical solutions for simple examples.
What is the concept of stream function and stream lines introduced in the chapter?
-The concept of stream function and stream lines is introduced as a way to visualize the flow field in two dimensions. Stream lines are paths that are instantaneously tangent to the velocity of the fluid at a particular moment.
How can the differential analysis of fluid flow be simplified using the concept of control volume?
-Differential analysis can be simplified by treating the flow field as a series of small control volumes, which when analyzed, can provide an overview of the entire flow without needing to know the details at each point within the control volume.
What are the main objectives to be achieved after studying the chapter on differential analysis of fluid flow?
-The main objectives include understanding how to derive the differential equations of conservation of mass and momentum, calculating stream functions and pressure fields, plotting streamlines for known velocity fields, and obtaining analytical solutions for simple flow scenarios.
What is the significance of the control volume approach in analyzing fluid flow?
-The control volume approach allows for the analysis of fluid flow by considering the flow through a specific volume, which can be used to calculate overall parameters like flow rate, mass inflow and outflow, and resultant forces without needing detailed information about the flow at each point within the volume.
How does the differential analysis involve the application of fluid dynamics equations?
-Differential analysis involves applying the differential equations of fluid motion to every point in the flow field, which is referred to as the domain of flow. This approach considers the flow as an analysis of millions of small control volumes arranged sequentially and stacked upon each other throughout the flow field.
What is the role of the Reynolds Transport Theorem in deriving the differential equations for fluid flow?
-The Reynolds Transport Theorem is used to derive the general form of the conservation of mass equation applied to a control volume, allowing the transformation of volume integrals of vector divergences into surface integrals, which simplifies the derivation of the differential form of the conservation equations.
How are the continuity and momentum equations simplified for incompressible flow?
-For incompressible flow, the continuity equation can be simplified by assuming that the density is constant, and the momentum equations can be linearized by considering the flow to be steady and the changes in density and temperature to be negligible.
What is the difference between the divergence method and the differential control volume method in deriving the differential form of the conservation of mass?
-The divergence method applies the Divergence Theorem to transform volume integrals into surface integrals, while the differential control volume method involves considering a small control volume and using Taylor series to estimate the flow rates across its surfaces, leading to the differential form of the conservation of mass.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Description and Derivation of the Navier-Stokes Equations

MekFlu #2: Persamaan Bernoulli, Kontinuitas dan Kekekalan Energi

LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 3

The million dollar equation (Navier-Stokes equations)

MekFlu #1: Prinsip Persamaan Bernoulli
LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 4
5.0 / 5 (0 votes)