87. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO
Summary
TLDREn este vídeo tutorial de 'Mate, fácil', se explica cómo resolver una ecuación diferencial de segundo orden con coeficientes constantes y homogénea. Se propone una solución de la forma \( y = e^{rx} \), se derivan y se sustituyen en la ecuación original, conduciendo a la ecuación característica. A través de factorización, se resuelven los valores de \( r \) y se obtienen dos soluciones linealmente independientes. La solución general se expresa como una combinación de ambas soluciones, multiplicadas por constantes arbitrarias. Además, se invita a los espectadores a practicar con un ejercicio similar y se anima a la interacción a través de comentarios y sugerencias.
Takeaways
- 🧮 En este video se resolverá una ecuación diferencial de segundo orden con coeficientes constantes.
- 📊 La ecuación diferencial homogénea a resolver es: y'' + 4y' + 3y = 0.
- 🔧 El primer paso es proponer una solución de la forma y = e^(rx) y sustituirla en la ecuación diferencial.
- 📉 Al sustituir las derivadas, se obtiene una ecuación algebraica llamada ecuación característica.
- ✏️ La ecuación característica es r² + 4r + 3 = 0, una ecuación de segundo grado.
- 📐 Esta ecuación se puede resolver fácilmente mediante factorización: (r + 1)(r + 3) = 0.
- 🧑🏫 Las soluciones para r son r = -1 y r = -3, lo que permite obtener dos soluciones linealmente independientes.
- 📝 La solución general de la ecuación diferencial es: y = c1 * e^(-x) + c2 * e^(-3x).
- 🔍 Se deja un ejercicio similar al espectador: resolver la ecuación diferencial y'' - 10y = 0.
- 👍 Se invita a los espectadores a suscribirse al canal y dejar preguntas o sugerencias en los comentarios.
Q & A
¿Cuál es la ecuación diferencial de segundo orden que se resuelve en el vídeo?
-La ecuación diferencial de segundo orden que se resuelve es \( y'' + 4y' + 3y = 0 \).
¿Qué método se utiliza para resolver la ecuación diferencial mencionada?
-Se utiliza el método de la ecuación característica para resolver la ecuación diferencial de segundo orden.
¿Cómo se propone una solución inicial para la ecuación diferencial?
-Se propone una solución de la forma \( y = e^{rx} \) y se sustituye en la ecuación diferencial para calcular las derivadas y simplificar.
¿Qué es la ecuación característica y cómo se obtiene?
-La ecuación característica es una ecuación algebraica que se obtiene de la ecuación diferencial al sustituir \( y = e^{rx} \), \( y' = re^{rx} \) y \( y'' = r^2e^{rx} \) y simplificar.
¿Cómo se resuelve la ecuación característica para la ecuación diferencial dada?
-Se resuelve la ecuación característica \( r^2 + 4r + 3 = 0 \) mediante factorización, encontrando los valores de \( r \) que satisfacen la ecuación.
¿Cuáles son los valores de \( r \) que se obtienen al resolver la ecuación característica?
-Los valores de \( r \) que se obtienen son \( r = -1 \) y \( r = -3 \).
¿Qué significan los valores de \( r \) en el contexto de la ecuación diferencial?
-Los valores de \( r \) representan las soluciones exponenciales de la ecuación diferencial, y son los exponentes de las soluciones particulares.
¿Cómo se determina la solución general de la ecuación diferencial?
-La solución general se determina como una combinación lineal de las soluciones particulares, que son \( c_1e^{-x} \) y \( c_2e^{-3x} \), donde \( c_1 \) y \( c_2 \) son constantes arbitrarias.
¿Por qué son necesarias dos soluciones linealmente independientes para la solución general?
-Son necesarias dos soluciones linealmente independientes para asegurar que la solución general abarque todo el espacio solución de la ecuación diferencial de segundo orden.
¿Cómo se relaciona la ecuación diferencial resuelta con las ecuaciones diferenciales de coeficientes constantes y homogéneas?
-La ecuación diferencial resuelta es un ejemplo de una ecuación diferencial de coeficientes constantes y homogénea, lo que significa que los coeficientes de las derivadas no dependen de la variable independiente y no hay términos no homogéneos.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
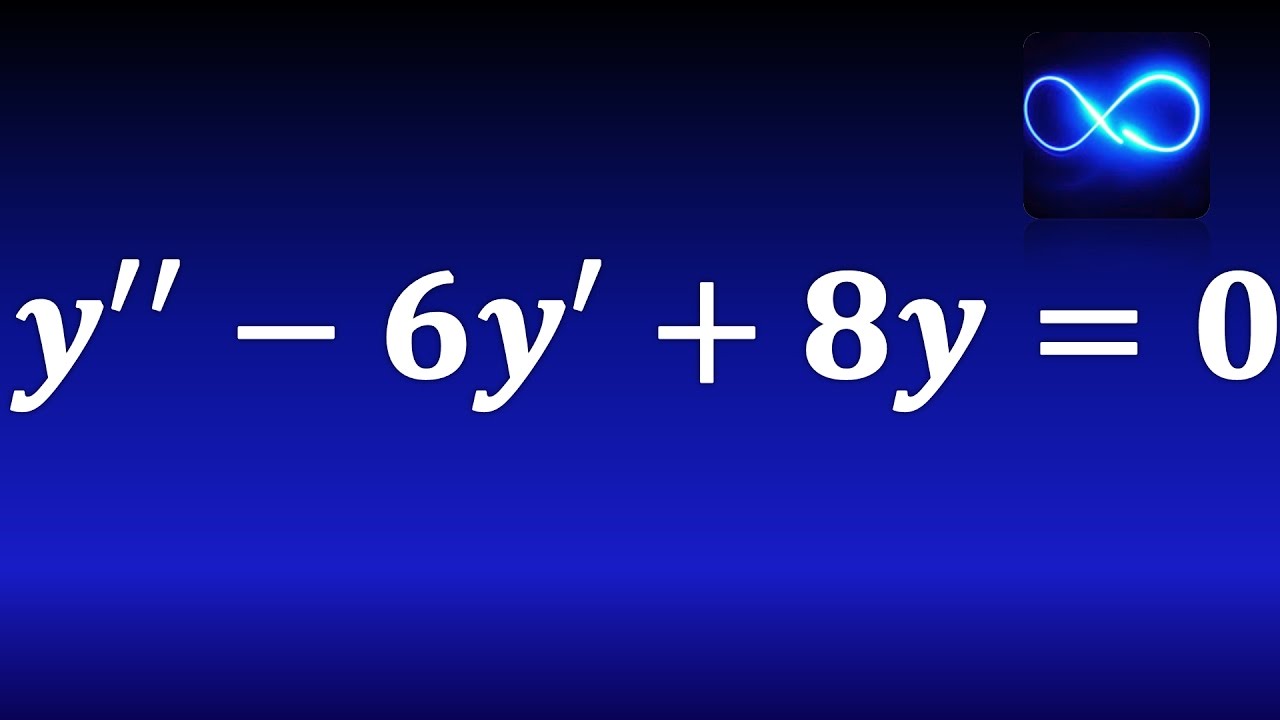
86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO

96. Ecuación diferencial de coeficientes constantes, raíces repetidas. EJERCICIO RESUELTO.
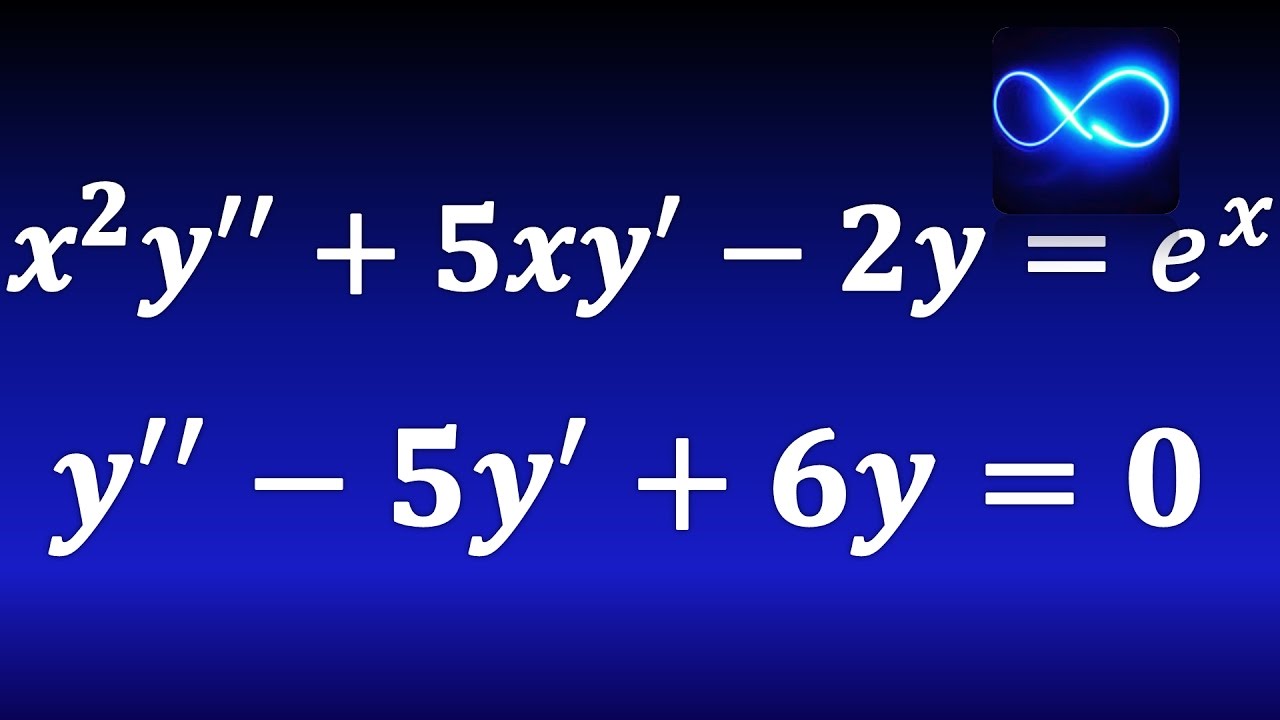
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes

1. Ecuación diferencial de variables separables

01. Modelo simple de población, Ecuaciones Diferenciales

90. Ecuación diferencial de coeficientes constantes (Con una raíz igual a cero) EJERCICIO RESUELTO
5.0 / 5 (0 votes)
